人教版数学九年级全册知识点训练营——弦切角定理模型及阿基米德折弦定理模型

试卷更新日期：2024-10-28 类型：复习试卷

进入出卷网下载

一、弦切角定理

1. 如图，AB是⊙O的弦，AC与⊙O相切于点A，且∠BAC=52°．

(1)、求∠OBA的度数；

(2)、求∠D的度数．

查看试题解析
2. 如图，AD与⊙O相切于点D，点A在直径CB的延长线上．

(1)、求证：∠DCB＝∠ADB；

(2)、若∠DCB＝30°，AC＝3 $\sqrt{3}$ ，求AD的长．

查看试题解析
3. 如图，AB是 $⊙ O$ 的直径，BC与 $⊙ O$ 相切，切点为B，AC与 $⊙ O$ 相交于点D，点E是 $\overset{⌢}{A D}$ 上任一点．

(1)、求证： $∠ B E D = ∠ D B C$ ．

(2)、已知 $A D = C D = 3$ ，求阴影部分的面积．（结果保留 $π$ ）

查看试题解析
4. 已知，如图，直线MN交⊙O于A，B两点，AC是直径，DE与⊙O相切于点D，过D点作DE⊥MN于点E．

(1)、求证：AD平分∠CAE；

(2)、若AE＝2，AD＝4，求⊙O的半径．

查看试题解析
5. 如图， $△$ ABC中，∠ACB＝90°，点O在边AC上，经过点C的⊙O与斜边AB相切于点D，交AC边于点E．

(1)、求证：∠ACD＝ $\frac{1}{2}$ ∠B；

(2)、若BC＝6，AC＝8，求AD、CD的长．

查看试题解析
6. 顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角．如图①所示：PA切⊙O于点A，AB是⊙O的一条弦，∠PAB就是⊙O的一个弦切角．经研究发现：弦切角等于它夹弧所对的圆周角．根据下面的“已知”和“求证”，写出“证明”过程，并回答后面的问题．

(1)、如图1，PA是⊙O的切线，A为切点，AC为直径，∠PAB夹弧所对的圆周角为∠C．求证：∠PAB＝∠C．

(2)、如图2，PA是⊙O的切线，A为切点，∠PAB夹弧所对的圆周角为∠D．求证：∠PAB＝∠D．

(3)、如图3，AB为半⊙O的直径，O为圆心，C，D为半⊙O上两点，过点C作半⊙O的切线CE交AD的延长线于点E，若CE⊥AD，且BC＝1，AB＝3，求DE的长．

查看试题解析
7. 如图，以AB为直径的⊙O与AC相切于点A，点D、E在⊙O上，连接AE、ED、DA，连接BD并延长交AC于点C，AE与BC交于点F．

(1)、求证：∠DAC=∠DEA；

(2)、若点E是BD的中点，⊙O的半径为3，BF=2，求AC的长．

查看试题解析
8. 如图，AB与⊙O相切于点B，AO及AO的延长线分别交⊙O于D、C两点，若∠A=40°，求∠C的度数.

查看试题解析
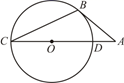9. 阅读资料：我们把顶点在圆上，并且一边和圆相交、另一边和圆相切的角叫做弦切角，如图1∠ABC所示．同学们研究发现：P为圆上任意一点，当弦AC经过圆心O时，且AB切⊙O于点A，此时弦切角∠CAB=∠P（图2）
证明：∵AB切⊙O于点A，∴∠CAB=90°，又∵AC是直径，∴∠P=90°∴∠CAB=∠P

问题拓展：若AC不经过圆心O（如图3），该结论：弦切角∠CAB=∠P还成立吗？请说明理由．

知识运用：如图4，AD是△ABC中∠BAC的平分线，经过点A的⊙O与BC切于点D，与AB、AC分别相交于E、F．求证：EF∥BC．

查看试题解析
10. 请阅读下列材料，并完成相应的任务．
人类会作圆并且真正了解圆的性质是在2000多年前，由我国的墨子给出圆的概念：“一中同长也．”．意思说，圆有一个圆心，圆心到圆周的长都相等．这个定义比希腊数学家欧几里得给圆下的定义要早100年．与圆有关的定理有很多，弦切角定理就是其中之一．
我们把顶点在圆上，一边和圆相交，另一边和圆相切的角叫做弦切角．
弦切角定理：弦切角的度数等于它所夹弧所对的圆周角度数．
下面是弦切角定理的部分证明过程：
证明：如图①，AB与⊙O相切于点A．当圆心O在弦AC上时，容易得到∠CAB＝90°，所以弦切角∠BAC的度数等于它所夹半圆所对的圆周角度数．
如图②，AB与⊙O相切于点A ，当圆心O在∠BAC的内部时，过点A作直径AD交⊙O于点D ，在 $\hat{A C}$ 上任取一点E ，连接EC ， ED ， EA ，则∠CED＝∠CAD．
任务：

(1)、请按照上面的证明思路，写出该证明的剩余部分；

(2)、如图③，AB与⊙O相切于点A．当圆心O在∠BAC的外部时，请写出弦切角定理的证明过程．

查看试题解析

11. 阅读以下材料，并完成相应的任务：

定义：顶点在圆上，一边与圆相交，另一边与圆相切的角叫做弦切角．弦切角定理：弦切角等于它所夹的弧所对的圆周角．

下面是该定理的部分证明过程：

已知：如图， $A B$ 与 $⊙ O$ 相切于点A ，点 $C$ ， $D$ 在 $⊙ O$ 上，连接 $A C$ ， $C D$ ， $A D$ ．

求证： $∠ C A B = ∠ D$ ．

证明：连接 $A O$ 并延长，交 $⊙ O$ 于点 $E$ ，连接 $C E$ ．

$∵ A B$ 与 $⊙ O$ 相切于点A

$∴ ∠ E A B = 9 0^{∘}$ （依据1）

$∴ ∠ E A C + ∠ C A B = 90 °$

$∵ A E$ 是 $⊙ O$ 的直径

$∴ ∠ E C A = 90 °$ （依据2）

$∴ ∠ E + ∠ E A C = 90 °$

任务：

(1)、上述证明过程中的“依据1”、“依据2”分别是指什么？

依据1：

依据2：

(2)、请按照上面的证明思路，写出该证明的剩余部分．

(3)、已知图中

⊙ O

的半径2，弦切角

∠ C A B = 30 °

，直接写出

A C

的长．

查看试题解析

二、阿基米德折弦定理

12. 请阅读下列材料，并完成相应的任务：阿基米德折弦定理，阿基米德（公元前287年一公元前212年），伟大的古希腊哲学家、百科式科学家、数学家、物理学家、力学家，静态力学和流体静力学的奠基人，并且享有“力学之父”的美称，阿基米德和高斯，牛顿并列为世界三大数学家．
阿拉伯Al-Binmi（973年一1050年）的译文中保存了阿基米德折弦定理的内容，苏联在1964年根据Al-Binmi译本出版了俄文版《阿基米德全集》，第一题就是阿基米德折弦定理．
阿基米德折弦定理：如图1，AB和BC是⊙O的两条弦（即折线ABC是圆的一条折弦），BC＞AB，M是 $\overset{⌢}{A B C}$ 的中点，则从M向BC所作垂线的垂足D是折弦ABC的中点，即CD＝AB+BD．
小明同学运用“截长法”和三角形全等来证明CD＝AB+BD，过程如下：
证明：如图2所示，在CB上截取CG＝AB，连接MA，MB，MC和MG．
∵M是 $\overset{⌢}{A B C}$ 的中点，∴MA＝MC，…

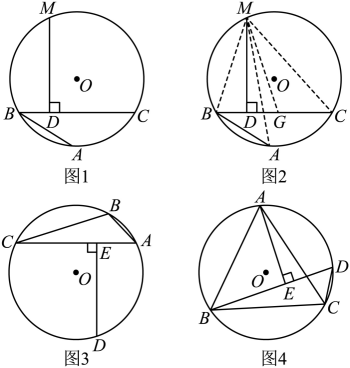(1)、请按照上述思路，写出该证明的剩余部分；

(2)、如图3，在⊙O中，BD =CD，DE⊥AC，若AB = 4，AC = 10，则AE的长度为；

(3)、如图4，已知等边 $△$ ABC内接于⊙O，AB = 8，D为 $\overset{⌢}{A C}$ 上一点，∠ABD = 45°，AE⊥BD于点E，求 $△$ BDC的周长．

查看试题解析
13. 请阅读以下材料，并完成相应的任务
【阅读材料】在《阿基米德全集》中的《引理集》中记述了伟大的古希腊数学家、哲学家、物理学家阿基米德提出的六个有关圆的引理，其中第二个引理是：
如图1，点P是弧 $A B$ 的任意一点， $P C ⊥ A B$ 于点C，点D在弦 $A B$ 上且 $A C = C D$ ，在弧 $A B$ 上取一点Q，使弧 $P Q$ =弧 $P A$ ，连接 $B Q$ ，则有 $B Q = B D$ .

(1)、如图2，小明同学尝试说明“ $B Q = B D$ ”，于是他连接了 $P A$ ， $P B$ ， $P D$ ， $P Q$ ，请根据小明的思路完成后续证明过程；

(2)、如图3，以 $A B$ 为直径的半圆上有一点P， $A P = 6 ， A B = 10$ ，直线l与 $⊙ O$ 相切于点P，过点 $B E ⊥ l$ 于点E，交 $⊙ O$ 于点Q，求出 $B Q$ 的长.

查看试题解析
14. 阿基米德（ $Archimedes$ ，公元前287年~公元前212年，古希腊）是有史以来最伟大的数学家之一．他与牛顿、高斯并称为三大数学王子．阿拉伯 $A1-Biruni$ （973年~1050年）的译文中保存了阿基米德折弦定理的内容，前苏联在1964年根据 $A1-Biruni$ 译本出版了俄文版《阿基米德全集》，第一题就是阿基米德的折弦定理．
阿基米德折弦定理：如图①，已知 $A B$ 和 $B C$ 是 $⊙ O$ 的两条弦（即折线 $A B C$ 是 $⊙ O$ 的一条折弦）， $B C > A B ， M$ 是 $\overset{⌢}{A B C}$ 的中点．那么从 $M$ 向 $B C$ 所作垂线的垂足 $D$ 是折弦 $A B C$ 的中点，即 $C D = A B + B D$ ．
下面是运用“截长法”证明 $C D = A B + B D$ 的部分证明思路：
证明：如图②，在 $C B$ 上截取 $C G = A B$ ，连接 $M A ， M B$ ，……
……

(1)、（定理证明）
按照上面的思路，写出剩余部分的证明过程．

(2)、（问题解决）
如图③，等边 $Δ A B C$ 内接于 $⊙ O ， A B = 3 ， D$ 为 $\overset{⌢}{A C}$ 上一点， $∠ A C D = 45 °$ ．
求 $Δ B D C$ 的周长．

查看试题解析