人教版数学九年级全册知识点训练营——圆与函数方程
试卷更新日期:2024-10-28 类型:复习试卷
一、夯实基础
-
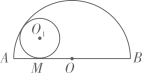
1. 用一个圆心角为(为常数,)的扇形作圆锥的侧面,记扇形的半径为 , 所作的圆锥的底面圆的周长为l,侧面积为 , 当在一定范围内变化时,与都随的变化而变化,则l与与满足的函数关系分别是( )A、一次函数关系,一次函数关系 B、二次函数关系,二次函数关系 C、一次函数关系,二次函数关系 D、二次函数关系,一次函数关系2. 如图,半圆O的直径AB=4,与半圆O内切的动圆O1与AB切于点M,设⊙O1的半径为y,AM=x,则y关于x的函数关系式是 ()
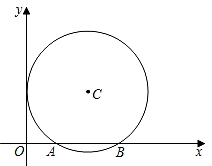
 A、 B、 C、 D、3. 已知,⊙O的半径是一元二次方程x2﹣5x﹣6=0的一个根,圆心O到直线l的距离d=4,则直线l与⊙O的位置关系是( )A、相交 B、相切 C、相离 D、平行4. 已知方程x2-7x+12=0的两根恰好是一个直角三角形的两条直角边的长,则这个直角三角形的外接圆的直径为( )A、2.5 B、6 C、5 D、5. 已知 和 的半径长分别是方程 的两根,且 ,则 和 的位置关系为( )A、相交 B、内切 C、内含 D、外切6. 如图,在平面直角坐标系中,⊙P的圆心是( , a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为2 ,则a的值是( )
A、 B、 C、 D、3. 已知,⊙O的半径是一元二次方程x2﹣5x﹣6=0的一个根,圆心O到直线l的距离d=4,则直线l与⊙O的位置关系是( )A、相交 B、相切 C、相离 D、平行4. 已知方程x2-7x+12=0的两根恰好是一个直角三角形的两条直角边的长,则这个直角三角形的外接圆的直径为( )A、2.5 B、6 C、5 D、5. 已知 和 的半径长分别是方程 的两根,且 ,则 和 的位置关系为( )A、相交 B、内切 C、内含 D、外切6. 如图,在平面直角坐标系中,⊙P的圆心是( , a)(a>2),半径为2,函数y=x的图象被⊙P截得的弦AB的长为2 ,则a的值是( ) A、2
A、2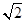 B、2+
B、2+ 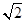 C、2
D、2+
7. 在⊙O中,弦AB和CD相交于点P,若PA=4,PB=7,CD=12,则以PC、PD的长为根的一元二次方程为( )A、x2+12x+28=0 B、x2﹣12x+28=0 C、x2﹣11x+12=0 D、x2+11x+12=08. 如图所示,A,B,C为上三点(在内部),延长AO交BC于点.设 , 则关于的函数表达式为.
C、2
D、2+
7. 在⊙O中,弦AB和CD相交于点P,若PA=4,PB=7,CD=12,则以PC、PD的长为根的一元二次方程为( )A、x2+12x+28=0 B、x2﹣12x+28=0 C、x2﹣11x+12=0 D、x2+11x+12=08. 如图所示,A,B,C为上三点(在内部),延长AO交BC于点.设 , 则关于的函数表达式为.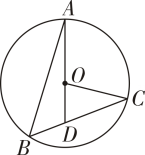 9. 一个直角三角形的两条边长是方程的两个根,则此直角三角形的外接圆的直径为 .
9. 一个直角三角形的两条边长是方程的两个根,则此直角三角形的外接圆的直径为 .二、能力提升
-
10. 如图, 中, , , , 是 的外接圆,点 是优弧 上任意一点(不包括点 , ),记四边形 的周长为 , 的长为 ,则 关于 的函数关系式是( )
 A、 B、 C、 D、11. 我国古代数学著作《增删算法统宗》记载“圆中方形”问题:“今有圆田一段,中间有个方池.丈量田地待耕犁,恰好三分在记,池面至周有数,每边三步无疑.内方圆径若能知,堪作算中第一.”其大意为:有一块圆形的田,中间有一块正方形水池,测量出除水池外圆内可耕地的面积恰好72平方步,从水池边到圆周,每边相距3步远.如果你能求出正方形边长和圆的直径,那么你的计算水平就是第一了.如图,设正方形的边长是x步,则列出的方程是 .
A、 B、 C、 D、11. 我国古代数学著作《增删算法统宗》记载“圆中方形”问题:“今有圆田一段,中间有个方池.丈量田地待耕犁,恰好三分在记,池面至周有数,每边三步无疑.内方圆径若能知,堪作算中第一.”其大意为:有一块圆形的田,中间有一块正方形水池,测量出除水池外圆内可耕地的面积恰好72平方步,从水池边到圆周,每边相距3步远.如果你能求出正方形边长和圆的直径,那么你的计算水平就是第一了.如图,设正方形的边长是x步,则列出的方程是 . 12. 如图,AB为⊙O的直径,点P为其半圆上任意一点(不含A、B),点Q为另一半圆上一定点,若∠POA为x°,∠PQB为y°,则y与x的函数关系是.
12. 如图,AB为⊙O的直径,点P为其半圆上任意一点(不含A、B),点Q为另一半圆上一定点,若∠POA为x°,∠PQB为y°,则y与x的函数关系是. 13. 如图,已知⊙O为△ABC的内切圆,D、E、F为切点,P是⊙O上异于E、F的一动点,若∠ A+∠C=x°,∠EPF=y°,则y与x的函数关系式为 .
13. 如图,已知⊙O为△ABC的内切圆,D、E、F为切点,P是⊙O上异于E、F的一动点,若∠ A+∠C=x°,∠EPF=y°,则y与x的函数关系式为 .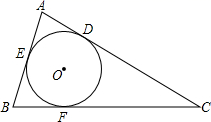
三、拓展创新
-
14. 如图所示,已知二次函数y=-x2+4x+5的图象与x轴交于A、B两点,与y轴交于点C,点P(m,n)是二次函数y=-x2+4x+5的图象上的一个动点,下面的m值不满足△ABP是钝角三角形的是( )
 A、2-2 B、-2 C、1.5+2 D、1+215. 如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )
A、2-2 B、-2 C、1.5+2 D、1+215. 如图,A点在半径为2的⊙O上,过线段OA上的一点P作直线l,与⊙O过A点的切线交于点B,且∠APB=60°,设OP=x,则△PAB的面积y关于x的函数图象大致是( )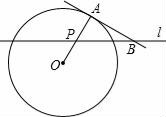 A、
A、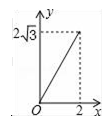 B、
B、 C、
C、 D、
D、 16. ⊙为等边的外接圆,半径为2,点在劣弧上运动(不与点 , 重合),连结 , , .则四边形的面积关于线段的长的函数解析式是.
16. ⊙为等边的外接圆,半径为2,点在劣弧上运动(不与点 , 重合),连结 , , .则四边形的面积关于线段的长的函数解析式是.