人教版数学九年级全册知识点训练营——圆中的折叠问题
试卷更新日期:2024-10-28 类型:复习试卷
一、夯实基础
-
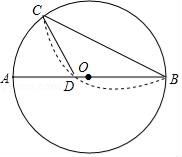
1. 如图,是圆O的弦, , 垂足为点C,将劣弧沿弦折叠交于的中点D,若 , 则圆O的半径为 .
二、能力提升
-
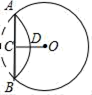
2. 如图,将半径为的沿折叠,恰好经过与垂直的半径的中点 , 则折痕长为( )
 A、 B、 C、 D、3. 如图,为圆形纸片圆周上的点,为直径,将该纸片沿折叠,使与交于点D,若的度数为 , 则的度数为( )
A、 B、 C、 D、3. 如图,为圆形纸片圆周上的点,为直径,将该纸片沿折叠,使与交于点D,若的度数为 , 则的度数为( ) A、 B、 C、 D、4. 把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则
A、 B、 C、 D、4. 把一张圆形纸片按如图所示方式折叠两次后展开,图中的虚线表示折痕,则 的度数是( )
的度数是( ) A、120° B、135° C、150° D、165°5. 如图,在圆心为 , 半径为的圆形纸片上画圆内接 , 再分别沿直线和折叠 , 和都经过圆心 , 则图中阴影部分的面积是( )
A、120° B、135° C、150° D、165°5. 如图,在圆心为 , 半径为的圆形纸片上画圆内接 , 再分别沿直线和折叠 , 和都经过圆心 , 则图中阴影部分的面积是( ) A、 B、 C、 D、6. 如图所示,将半径为5的半圆折叠,使得折过来的弧经过点 , 则折痕.
A、 B、 C、 D、6. 如图所示,将半径为5的半圆折叠,使得折过来的弧经过点 , 则折痕. 7. 如图,在扇形中,点在上,连接 , 将沿折叠得到 . 若 , 且与所在的圆相切于点 , 则 .
7. 如图,在扇形中,点在上,连接 , 将沿折叠得到 . 若 , 且与所在的圆相切于点 , 则 . 8. 如图,在中, , 点D、E分别在上,且 , 将沿着折叠,点C恰好落在边上的点F处,如果 , 那么的长为
8. 如图,在中, , 点D、E分别在上,且 , 将沿着折叠,点C恰好落在边上的点F处,如果 , 那么的长为 9. 如图,在中, , , 是上的动点,以为圆心,的长为半径作圆交于点 , 分别是上的点,将沿折叠,点与点恰好重合.
9. 如图,在中, , , 是上的动点,以为圆心,的长为半径作圆交于点 , 分别是上的点,将沿折叠,点与点恰好重合. (1)、如图1,若 , 证明与直线相切;(2)、如图2,若经过点 , 连接 .
(1)、如图1,若 , 证明与直线相切;(2)、如图2,若经过点 , 连接 .①的长是 ▲ ;
②判断四边形的形状,并证明.
三、拓展创新
-
10. 如图,正方形的边长为4,点是边上的一点,将沿着折叠至 , 若、恰好与正方形的中心为圆心的相切,则折痕的长为( )
 A、 B、5 C、 D、以上都不对11. 如图,在半圆O中,直径AB=2,C是半圆上一点,将弧AC沿弦AC折叠交AB于D , 点E是弧AD的中点.连接OE , 则OE的最小值为( )
A、 B、5 C、 D、以上都不对11. 如图,在半圆O中,直径AB=2,C是半圆上一点,将弧AC沿弦AC折叠交AB于D , 点E是弧AD的中点.连接OE , 则OE的最小值为( ) A、 B、 C、 D、12. 如图,AC是矩形ABCD的对角线,⊙O是△ABC的内切圆,现将矩形ABCD按如图所示的方式折叠,使点D与点O重合,折痕为FG,点F,G分别在AD,BC上,连结OG,DG,若OG⊥DG,且⊙O的半径长为1,则下列结论不成立的是( )
A、 B、 C、 D、12. 如图,AC是矩形ABCD的对角线,⊙O是△ABC的内切圆,现将矩形ABCD按如图所示的方式折叠,使点D与点O重合,折痕为FG,点F,G分别在AD,BC上,连结OG,DG,若OG⊥DG,且⊙O的半径长为1,则下列结论不成立的是( ) A、CD+DF=4 B、CD−DF=2−3 C、BC+AB=2+4 D、BC−AB=213. 如图,是半径为4的的弦,且 , 将沿着弦折叠,点C是折叠后的上一动点,连接并延长交于点D,点E是的中点,连接.则的最小值为 .
A、CD+DF=4 B、CD−DF=2−3 C、BC+AB=2+4 D、BC−AB=213. 如图,是半径为4的的弦,且 , 将沿着弦折叠,点C是折叠后的上一动点,连接并延长交于点D,点E是的中点,连接.则的最小值为 .
-