吉林省吉林市2017年中考数学二模试卷

试卷更新日期：2017-12-07 类型：中考模拟

进入出卷网下载

一、单项选择题

1. 2³表示（）

A、2×2×2 B、2×3 C、3×3 D、2+2+2

查看试题解析
2. 下列计算正确的是（）

A、2a+3b=5ab B、a³•a²=a⁶ C、a⁶÷a²=a⁴ D、（﹣2a³）²=﹣4a⁶

查看试题解析
3. 用6个完全相同的小正方体组合成如图所示的立体图形，它的左视图为（）

A、 B、 C、 D、

查看试题解析
4. 不等式组 ${\begin{matrix} x - 1 \leq 3 \\ 2 x > 6 \end{matrix}$ 的解集是（）

A、3＜x≤4 B、x≤4 C、x＞3 D、2≤x＜3

查看试题解析
5. 用配方法解方程x²﹣4x﹣1=0，方程应变形为（）

A、（x+2）²=3 B、（x+2）²=5 C、（x﹣2）²=3 D、（x﹣2）²=5

查看试题解析
6. 古埃及人曾经用如图所示的方法画直角：把一根长绳打上等距离的13个结，然后以3个结间距、4个结间距、5个结间距的长度为边长，用木桩钉成一个三角形，其中一个角便是直角，这样做的道理是（）

A、直角三角形两个锐角互补 B、三角形内角和等于180° C、如果三角形两条边长的平方和等于第三边长的平方 D、如果三角形两条边长的平方和等于第三边长的平方，那么这个三角形是直角三角形

查看试题解析
7. 如图，在△ABC中，点D、E分别在AB、AC边上，DE∥BC，若AD=1，BD=2，则 $\frac{D E}{B C}$ 的值为（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{9}$

查看试题解析
8. 如图，在平面直角坐标系中，点A（1， $\sqrt{3}$ ），若将点A绕点O顺时针旋转150°得到点B，则点B的坐标为（）

A、（0，2） B、（0，﹣2） C、（﹣1，﹣ $\sqrt{3}$ ） D、（ $\sqrt{3}$ ，1）

查看试题解析

二、填空题

9. 计算： $\sqrt{{(- 2)}^{2}}$ ﹣|﹣1|= ．

查看试题解析
10. 分式方程 $\frac{2}{x - 2}$ = $\frac{3}{x}$ 的解是．

查看试题解析
11. 篮球联赛中，每场比赛都要分出胜负，每队胜1场得2分，负1场得1分．某队在10场比赛中得到16分，设这个队胜x场，负y场，则x，y满足的方程组是．

查看试题解析
12. 如图，矩形ABCD的对角线AC，BD相交于点O，分别过点C，D作BD，AC的平行线，相交于点E．若AD=6，则点E到AB的距离是．

查看试题解析
13. 如图，这四边行ABCD中，点M、N分别在AB，CD边上，将四边形ABCD沿MN翻折，使点B、C分别在四边形外部点B₁ ， C₁处，则∠A+∠B₁+∠C₁+∠D= ．

查看试题解析
14. 在2×2的正方形网格中，每个小正方形的边长为1．以点O为圆心，2为半径画弧交图中网格线与点A，B，则弧AB的长是．

查看试题解析

三、解答题

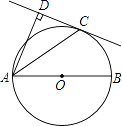
15. 先化简，再求值： $\frac{x^{2} - 4 x + 4}{x^{2} - 4}$ ÷ $\frac{x - 2}{x^{2} + 2 x}$ +3，其中x=﹣3.2．

查看试题解析
16. 不透明口袋中装有1个红球和2个白球，这些球除颜色外无其他差别．从口袋中随机摸出1个球，放回搅匀，再从口袋中随机摸出1个球，用画树枝状图或列表的方法，有两次摸到的球都是白球的概率．

查看试题解析
17. 如图，AB为⊙O的直径，C为⊙O上一点，AD和过点C的切线互相垂直，垂足为D．求证：AC平分∠DAB．

查看试题解析
18. 如图，反比例函数y= $\frac{k}{x}$ （x＞0）的图象与一次函数y=3x的图象相交于点A，其横坐标为2．

(1)、求k的值；

(2)、点B为此反比例函数图象上一点，其纵坐标为3．过点B作CB∥OA，交x轴于点C，直接写出线段OC的长．

查看试题解析

四、解答题

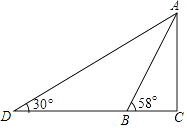
19. 如图，某游乐园有一个滑梯高度AB，高度AC为3米，倾斜角度为58°．为了改善滑梯AB的安全性能，把倾斜角由58°减至30°，调整后的滑梯AD比原滑梯AB增加多少米？（精确到0.1米）
（参考数据：sin58°=0.85，cos58°=0.53，tan58°=1.60）

查看试题解析
20. 利用图1，图2提供的某公司的一些信息，解答下列问题．

(1)、2016年该公司工资支出的金额是万元；

(2)、2014年到2016年该公司总支出的年平均增长率；

(3)、若保持这种增长速度，请你预估该公司2017年的总支出．

查看试题解析

五、解答题

21. 某网站策划了A、B两种上网的月收费方式：
收费方式
月使用费/元
包时上网时间/h
超时费/（元/min）
A
30
25
0.05
B
m
n
P
设每月上网学习时间为x（h）小时，方案A，B的收费金额分别为y_A（元）、y_B（元）．
如图是y_B与x之间函数关系的图象
（友情提示：若累计上网时间不超出“包时上网时间”，则只收”月使用费“；若累计上网时间不超出“包时上网时间”，则对超出部分再加收”超时费“）

(1)、m=；n=p= ．

(2)、写出y_A与x之间的函数关系式．

(3)、若每月上网的时间为29小时，请说明选取哪种方式能节省上网费？

查看试题解析
22. 如图，在Rt△ABC中，∠C=90°，∠A=30°．点D是AB中点，点E为边AC上一点，连接CD，DE，以DE为边在DE的左侧作等边三角形DEF，连接BF．

(1)、△BCD的形状为；

(2)、随着点E位置的变化，∠DBF的度数是否变化？并结合图说明你的理由；

(3)、当点F落在边AC上时，若AC=6，请直接写出DE的长．

查看试题解析

六、解答题

23. 如图，在Rt△ABC中，∠C=90°，AC=BC，AB=4cm，线段AB上一动点D，以1cm/s的速度从点A出发向终点B运动．过点D作DE⊥AB，交折线AC﹣CB于点E，以DE为一边，在DE左侧作正方形DEFG．设运动时间为x（s）（0＜x＜4）．正方形DEFG与△ABC重叠部分面积为y（cm²）．

(1)、当x=s时，点F在AC上；

(2)、求y关于x的函数解析式，并写出自变量x的取值范围；

(3)、设正方形DEFG的中心为点O，直接写出运动过程中，直线BO平分△ABC面积时，自变量x的取值范围．

查看试题解析
24. 如图，在平面直角坐标系中的两点A（m，0），B（2m，0）（m＞0），二次函数y=ax²+bx+m的图象与x轴交与A，B两点与y轴交于点C，顶点为点D．

(1)、当m=1时，直线BC的解析式为，二次函数y=ax²+bx+m的解析式为；

(2)、求二次函数y=ax²+bx+m的解析式为（用含m的式子表示）；

(3)、连接AC、AD、BD，请你探究 $\frac{S_{△ A O C}}{S_{△ A B D}}$ 的值是否与m有关？若有关，求出它与m的关系；若无关，说明理由；

(4)、当m为正整数时，依次得到点A₁ ， A₂ ， …，A_m的横坐标分别为1，2，…m；点B₁ ， B₂ ， …，B_m 的横坐标分别为2，4，…2m（m≤10）；经过点A₁ ， B₁ ，点A₂ ， B₂ ， …，点A_m ， B_m的这组抛物线y=ax²+bx+m分别与y轴交于点C₁ ， C₂ ， …，C_m ，由此得到了一组直线B₁C₁ ， B₂C₂ ， …，B_mC_m ，在点B₁ ， B₂ ， …，B_m 中任取一点B_n ，以线段OB_n为边向上作正方形OB_nE_nF_n ，若点E_n在这组直线中的一条直线上，直接写出所有满足条件的点E_n的坐标．

查看试题解析

收费方式	月使用费/元	包时上网时间/h	超时费/（元/min）
A	30	25	0.05
B	m	n	P