浙教版数学八年级上册期中模拟测试卷 C
试卷更新日期:2024-10-27 类型:期中考试
一、选择题(每题3分,共30分)
-
1. 数学中有许多精美的曲线,以下是“悬链线”“黄金螺旋线”“三叶玫瑰线”和“笛卡尔心形线”.其中不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 将一个含30°角的三角尺和直尺如图放置,若∠1=50°,则∠2的度数是( )
2. 将一个含30°角的三角尺和直尺如图放置,若∠1=50°,则∠2的度数是( ) A、30° B、40° C、50° D、60°3. 如图,在纸上画有∠AOB , 将两把直尺按图示摆放,直尺边缘的交点P在∠AOB的平分线上,则( )
A、30° B、40° C、50° D、60°3. 如图,在纸上画有∠AOB , 将两把直尺按图示摆放,直尺边缘的交点P在∠AOB的平分线上,则( ) A、d1与d2一定相等 B、d1与d2一定不相等 C、l1与l2一定相等 D、l1与l2一定不相等4. 如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心的光线相交于点 , 点为焦点.若 , 则的度数为( )
A、d1与d2一定相等 B、d1与d2一定不相等 C、l1与l2一定相等 D、l1与l2一定不相等4. 如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心的光线相交于点 , 点为焦点.若 , 则的度数为( )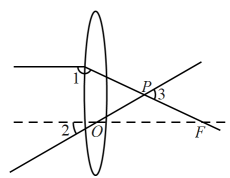 A、 B、 C、 D、5. 如图,在Rt△ABC中,∠ACB=90°,DE垂直平分AB交BC于点D , 若△ACD的周长为50cm , 则AC+BC=( )
A、 B、 C、 D、5. 如图,在Rt△ABC中,∠ACB=90°,DE垂直平分AB交BC于点D , 若△ACD的周长为50cm , 则AC+BC=( ) A、25cm B、45cm C、50cm D、55cm6. 如图,AB与CD相交于点 , 只添加一个条件,能判定的是( )
A、25cm B、45cm C、50cm D、55cm6. 如图,AB与CD相交于点 , 只添加一个条件,能判定的是( ) A、 B、 C、 D、7. 如图,AB∥CD , 过点D作DE⊥AC于点E . 若∠D=50°,则∠A的度数为( )
A、 B、 C、 D、7. 如图,AB∥CD , 过点D作DE⊥AC于点E . 若∠D=50°,则∠A的度数为( ) A、130° B、140° C、150° D、160°8. 如图,圆柱的底面直径为AB,高为AC.一只蚂蚁在C处,沿圆柱的侧面爬到B处,现将圆柱侧面沿AC“剪开”,在侧面展开图上画出蚂蚁爬行的最近路线,正确的是( )
A、130° B、140° C、150° D、160°8. 如图,圆柱的底面直径为AB,高为AC.一只蚂蚁在C处,沿圆柱的侧面爬到B处,现将圆柱侧面沿AC“剪开”,在侧面展开图上画出蚂蚁爬行的最近路线,正确的是( )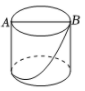 A、
A、 B、
B、 C、
C、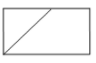 D、
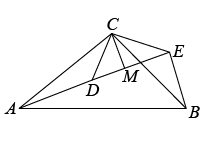
D、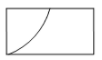 9. 如图1是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形.若 , , 则点B到的距离为( )
9. 如图1是第七届国际数学教育大会(ICME)会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形.若 , , 则点B到的距离为( )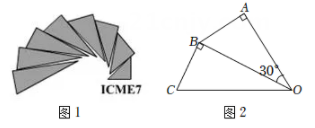 A、 B、 C、1 D、210. 不等式组 有3个整数解,则 的取值范围是( )
A、 B、 C、1 D、210. 不等式组 有3个整数解,则 的取值范围是( )
A、 B、 C、 D、二、填空题(每题3分,共18分)
-
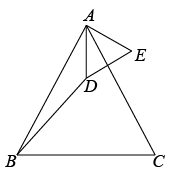
11. 对于实数a , b定义运算“※”为 , 例如 , 则关于x的不等式有且只有一个正整数解时,m的取值范围是.12. 如图,在中, , E是边上一点,连接 , 在右侧作 , 且 , 连接 . 若 , , 则四边形的面积为 .
 13. 如图,在△ABC中,AB=AC , ∠A=36°,BD平分∠ABC交AC于点D . 若BC=2,则AD的长度为 .
13. 如图,在△ABC中,AB=AC , ∠A=36°,BD平分∠ABC交AC于点D . 若BC=2,则AD的长度为 . 14. 勾股数是指能成为直角三角形三条边长的三个正整数,世界上第一次给出勾股数公式的是中国古代数学著作《九章算术》.现有勾股数a , b , c , 其中 , 均小于 , , , 是大于1的奇数,则(用含的式子表示).15. 如图,等边三角形的边长为 , 动点P从点A出发以的速度沿向点B匀速运动,过点P作 , 交边于点Q,以为边作等边三角形 , 使点A,D在异侧,当点D落在边上时,点P需移动s.
14. 勾股数是指能成为直角三角形三条边长的三个正整数,世界上第一次给出勾股数公式的是中国古代数学著作《九章算术》.现有勾股数a , b , c , 其中 , 均小于 , , , 是大于1的奇数,则(用含的式子表示).15. 如图,等边三角形的边长为 , 动点P从点A出发以的速度沿向点B匀速运动,过点P作 , 交边于点Q,以为边作等边三角形 , 使点A,D在异侧,当点D落在边上时,点P需移动s. 16. 如图,直线 , 直线 , 则°.
16. 如图,直线 , 直线 , 则°.
三、解答题(共10题,共72分)
-
17. 解不等式组,并把解集在数轴上表示出来18. 解不等式组 , 并求出它的所有整数解的和.19. 如图,在四边形中, , .
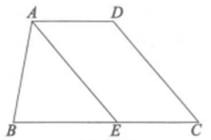 (1)、求的度数;(2)、平分交于点 , .求证:.20. 如图,AC平分 , 垂足分别为B,D.
(1)、求的度数;(2)、平分交于点 , .求证:.20. 如图,AC平分 , 垂足分别为B,D. (1)、求证:;(2)、若 , 求四边形ABCD的面积.21. 如图, , , , 垂足分别为 , .
(1)、求证:;(2)、若 , 求四边形ABCD的面积.21. 如图, , , , 垂足分别为 , .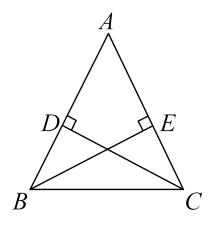 (1)、求证:;(2)、若 , , 求的长.22. 创建文明城市,构建美好家园.为提高垃圾分类意识,幸福社区决定采购A,B两种型号的新型垃圾桶.若购买3个A型垃圾桶和4个B型垃圾桶共需要580元,购买6个A型垃圾桶和5个B型垃圾桶共需要860元.(1)、求两种型号垃圾桶的单价;(2)、若需购买A,B两种型号的垃圾桶共200个,总费用不超过15000元,至少需购买A型垃圾桶多少个?23. 如图,在中,为的角平分线.以点圆心,长为半径画弧,与分别交于点 , 连接 .
(1)、求证:;(2)、若 , , 求的长.22. 创建文明城市,构建美好家园.为提高垃圾分类意识,幸福社区决定采购A,B两种型号的新型垃圾桶.若购买3个A型垃圾桶和4个B型垃圾桶共需要580元,购买6个A型垃圾桶和5个B型垃圾桶共需要860元.(1)、求两种型号垃圾桶的单价;(2)、若需购买A,B两种型号的垃圾桶共200个,总费用不超过15000元,至少需购买A型垃圾桶多少个?23. 如图,在中,为的角平分线.以点圆心,长为半径画弧,与分别交于点 , 连接 .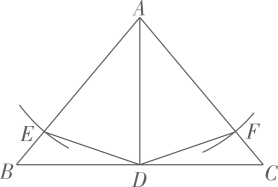 (1)、求证:;(2)、若 , 求的度数.24. 如图,在中 , 过点C作 , 在上截取 , 上截取 , 连接 .
(1)、求证:;(2)、若 , 求的度数.24. 如图,在中 , 过点C作 , 在上截取 , 上截取 , 连接 .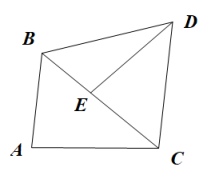 (1)、求证:;(2)、若 , 求的面积.
(1)、求证:;(2)、若 , 求的面积.