垂美四边形模型—北师大版数学八（上）知识点训练

试卷更新日期：2024-10-27 类型：复习试卷

进入出卷网下载

一、选择题

1. 对角线互相垂直的四边形叫做“垂美”四边形，现有如图所示的“垂美”四边形ABCD ，对角线AC ， BD交于点O ．若 $A D = 1$ ， $B C = 4$ ，则 $A B^{2} + C D^{2}$ 等于（）

A、15 B、16 C、17 D、20

查看试题解析

二、填空题

2. 对角线互相垂直的四边形叫做“垂美”四边形，现有如图所示的“垂美”四边形 $A B C D$ ，对角线 $A C 、 B D$ 交于点O．若 $A D = 2 ， B C = 4$ ，则 $A B^{2} + C D^{2} =$ ．

查看试题解析
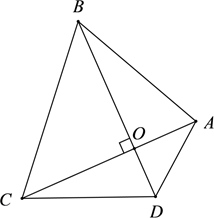3. 对角线互相垂直的四边形叫做“垂美”四边形，如图所示的“垂美”四边形 $A B C D$ 的对角线 $A C$ ， $B D$ 交于点 $D$ ，若 $A B = 5$ ， $C D = 4$ ，则 $A D^{2} + B C^{2}$ ＝．

查看试题解析

三、实践探究题

4. 我们把对角线互相垂直的四边形称为“垂美四边形”．如图1，已知四边形 $A B C D$ ， $A C ⊥ B D$ ，像这样的四边形称为“垂美四边形”．

(1)、探索证明
如图1，设 $A B = a$ ， $B C = b$ ， $C D = c$ ， $A D = d$ ，猜想 $a^{2}$ ， $b^{2}$ ， $c^{2}$ ， $d^{2}$ 之间的关系，用等式表示出来，并说明你的理由．

(2)、变式思考
如图2， $B D$ ， $C E$ 是 $△ A B C$ 的中线， $B D ⊥ C E$ ，垂足为O ， $B C = 2 D E$ ，设 $B C = m$ ， $A C = n$ ， $A B = k$ ，请用一个等式把 $m^{2}$ ， $n^{2}$ ， $k^{2}$ 三者之间的数量关系表示出来：．

(3)、拓展应用
如图3，在长方形 $A B C D$ 中，E为 $A D$ 的中点，若四边形 $A B C E$ 为“垂美四边形”，且 $B C = 2$ ，求 $A B$ 的长．

查看试题解析
5. 如图1，我们把对角线互相垂直的四边形叫做垂美四边形．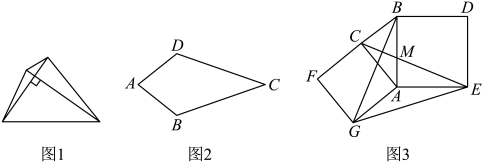

(1)、概念理解：我们已经学习了平行四边形、菱形、矩形、正方形，在这四种图形中是垂美四边形的是．

(2)、性质探究：如图2，已知四边形 $A B C D$ 是垂美四边形，求证： $A D^{2} + B C^{2} = A B^{2} + C D^{2}$ ．

(3)、问题解决：如图3，分别以 $R t △ A C B$ 的直角边 $A C$ 和斜边 $A B$ 为边向外作正方形 $A C F G$ 和正方形 $A B D E$ ，连接 $C E$ ， $B G$ ， $G E$ ， $C E$ 交 $A B$ 于点 $M$ ，已知 $A C = 4$ ， $A B = 5$ ，求 $G E$ 的长．

查看试题解析