勾股定理在网格中的应用—北师大版数学八（上）知识点训练

试卷更新日期：2024-10-27 类型：复习试卷

进入出卷网下载

一、基础夯实

1. 如图，在3×3的正方形网格中，每个小正方形边长为1，点A，B，C，D均为格点，以A为圆心，AB长为半径作弧，交网格线CD于点E，则C，E两点间的距离为（）

A、 $\sqrt{3}$ B、3- $\sqrt{3}$ C、 $\frac{\sqrt{3} + 1}{2}$ D、 $\sqrt{3}$ - $\frac{1}{2}$

查看试题解析
2. 如图，在 $3 \times 3$ 的正方形网格中，若小正方形的边长是1，则任意两个格点间的距离不可能是（）

A、 $\sqrt{7}$ B、 $\sqrt{8}$ C、 $\sqrt{9}$ D、 $\sqrt{10}$

查看试题解析
3. 如图，已知网格中每个小正方形的边长均为1，以点A为圆心，AB为半径画弧交网格线于点D，则ED的长为（）

A、 $\sqrt{5}$ B、3 C、2 D、 $\sqrt{13}$

查看试题解析
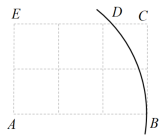4. 如图，在四个均由十六个小正方形组成的正方形网格中，各有一个三角形，那么这四个三角形中，不是直角三角形的是（）

A、 B、 C、 D、

查看试题解析
5. 在正方形网格中画格点 $△ A B C$ ，如图，若网格中每个小正方形的边长均为 $1$ ，则下列说法错误的是（）

A、 $∠ A C B = 90 °$ B、 $B C = \sqrt{5}$ C、 $A B = 2 B C$ D、 $A C^{2} + B C^{2} = A B^{2}$

查看试题解析
6. 如图： $4 \times 1$ 网格中每个正方形边长为1，表示 $\sqrt{5}$ 长的线段是（）

A、 $O A$ B、 $O B$ C、 $O C$ D、 $O D$

查看试题解析
7. 如图，在由边长为1个单位长度的小正方形组成的网格中，线段 $A B$ 的两个端点都在正方形网格的格点上，则 $A B$ 的长度可能是（）

A、 $\sqrt{3}$ B、 $\sqrt{5}$ C、 $\sqrt{6}$ D、 $\sqrt{7}$

查看试题解析
8. 如图， $△ A B C$ 的顶点 $A ， B ， C$ 在边长为 $1$ 的正方形网格的格点上， $C D ⊥ A B$ 于点 $D$ ．则 $C D$ 的长为．

查看试题解析
9. 如图，网格中每个小正方形的边长均为1，点 $A, B, C, E$ 均在小正方形的顶点上．以点 $A$ 为圆心， $A B$ 长为半径画弧，圆弧交 $C E$ 于点 $D$ ，则 $E D$ 的长为．

查看试题解析
10. 如图，正方形网格中的每个小正方形边长都为1，小格的顶点叫做格点，其中格点 A已在网格中标出，以格点为顶点按下列要求画图．

(1)、在网格中画 $△ A B C$ ，使 $A B = \sqrt{10}$ ， $A C = 4$ ， $B C = 3 \sqrt{2}$ ；

(2)、请你用所学的知识验证（1）中所画的 $△ A B C$ 是不是直角三角形．

查看试题解析
11. 如图所示的 $4 \times 4$ 网格是正方形网格，顶点是网格线交点的三角形称为格点三角形．如图1， $△ A B C$ 为格点三角形．

(1)、 $∠ A B C =$ __________ $°$ ；

(2)、在图2和图3中分别画出一个以点 $C_{1}$ ， $C_{2}$ 为顶点，与 $△ A B C$ 全等，且位置互不相同的格点三角形．

查看试题解析
12. 作图题．
下图是一个边长为 1 的正方形网格图，请在网格图中画出一个边长为 $2 \sqrt{2} ， \sqrt{5}$ 和 3 的三角形．(要求三角形的顶点在格点处)

查看试题解析

二、能力提升

13. 如图是由单位长度均为1的小正方形组成的网格，A，B，C，D都是网格线的交点，由其中任意三个点连接而成的三角形是直角三角形的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
14. 如图，在边长为1的小正方形网格中， $P$ 为 $C D$ 上任意一点， $(P B + P A) (P B - P A)$ 的值为（）

A、6 B、8 C、10 D、12

查看试题解析
15. 如图，在单位正方形组成的网格图中标有AB、CD、EF、GH四条线段，其中能构成一个直角三角形三边的线段是（　　）

A、CD、EF、GH B、AB、EF、GH C、AB、CD、GH D、AB、CD、EF

查看试题解析
16. 如图，A ， B ， C ， O四点都在3×3正方形网格的格点上，则∠AOB－∠BOC＝°．

查看试题解析
17. 如图，在下列网格中，小正方形的边长均为1，点 $A$ 、 $B$ 、 $O$ 都在格点上，则 $∠ A O B$ 的度数为．

查看试题解析
18. 如图，在4x3正方形网格中，每个小正方形的边长都是1．

(1)、分别求出线段AB、CD的长度；

(2)、在图中画出线段EF、使得EF的长为 $\sqrt{5}$ ，以AB、CD、EF三条线段能否构成直角三角形，并说明理由.

查看试题解析
19. 如图，在 $8 \times 6$ 的网格中，每个小正方形的边长均为一个单位长度， $△ A B C$ 的三个顶点都在格点上，只用无刻度的直尺，在给定的网格中，按下列要求作图，保留作图痕迹．

(1)、 $A B =$ ；

(2)、在图1中确定一点D ，点D在边 $B C$ 上，使 $A B = B D$ ；

(3)、在图2中确定一点E ，点E在边 $A C$ 上，使 $B E$ 平分 $∠ A B C$ ．

查看试题解析
20. 如图是若干个边长为1个单位长度的小正方形组成的网格，一只小虫从A点出发，沿着A-B-C-D-E-F的路径到F点取食，请你计算一下，它一共走了多少路程．(写出计算过程)

查看试题解析

三、拓展创新

21. 学习几何时，通常是先用几何的眼光去观察，再用代数的方法去验证 $.$ 网格是研究几何图形的一种工具，也是培养几何直观的一种方式．

(1)、如图是正方形网格，正方形的顶点称为格点，每一个小正方形的边长为 $1$ ．
$①$ 如图 $1$ ，点 $A$ 、 $B$ 在格点上，仅用无刻度的直尺找出线段 $A B$ 的中点 $O ($ 不写画法，保留画图痕迹 $)$ ；
$②$ 如图 $2$ ，点 $A$ 、 $B$ 、 $C$ 在格点上，仅用无刻度的直尺找出 $∠ A$ 的平分线交 $B C$ 于点 $P$ ，并写出画图的步骤或依据；

(2)、如图 $3$ ，在 $△ A B C$ 中， $A B = 1$ ， $A C = 2$ ， $B C = \sqrt{5}$ ，以 $A C$ 为边在 $A C$ 的左侧作等腰直角 $△ A C D$ ，连接 $B D$ ，求 $B D$ 的长．

查看试题解析