湖北省武汉四十一中2017年中考数学模拟试卷
试卷更新日期：2017-12-07 类型：中考模拟
一、选择题：
-
1. 实际测量一座山的高度时，可在若干个观测点中测量每两个相邻可视观测点的相对高度，然后用这些相对高度计算出山的高度．下表是某次测量数据的部分记录（用A﹣C表示观测点A相对观测点C的高度）根据这次测量的数据，可得观测点A相对观测点B的高度是（ ）米．
A﹣C
C﹣D
E﹣D
F﹣E
G﹣F
B﹣G
90米
80米
﹣60米
50米
﹣70米
40米
A、210 B、130 C、390 D、﹣2102. 下列图形中，既是轴对称图形又是中心对称图形的是（ ）A、
B、
C、
D、
3. 13600000=1.36×10a ， 3590000=3.59×10b ， 那么（b﹣a）5=（ ）
A、1 B、﹣1 C、2 D、﹣24. 如图，在△ABC中，AB=AC=4，∠ABC和∠ACB的平分线交于点E，过点E作MN∥BC分别交AB，AC于M、N，则△AMN的周长为（ ）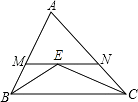
A、12 B、4 C、8 D、不确定5. 若（x﹣2）（x2+ax+b）的积中不含x的二次项和一次项，则a和b的值（ ）A、a=0；b=2 B、a=2；b=0 C、a=﹣1；b=2 D、a=2；b=46. 一个不透明的盒子中装有2个红球和1个白球，它们除颜色外都相同．若从中任意摸出一个球，则下列叙述正确的是（ ）A、摸到红球是必然事件 B、摸到白球是不可能事件 C、摸到红球比摸到白球的可能性相等 D、摸到红球比摸到白球的可能性大7. 如图所示正三棱柱的主视图是（ ）
A、
B、
C、
D、
8. 如图，AB 为⊙O 的切线，切点为 B，连接 AO 与⊙O 交与点 C，BD 为⊙O 的直径，连接 CD，若∠A=30°，OA=2，则图中阴影部分的面积为（ ）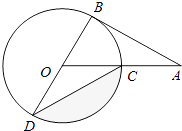
A、 B、 C、 D、9. 如图，把Rt△ABC放在直角坐标系内，其中∠CAB=90°，BC=5，点A，B的坐标分别为（1，0）、（4，0）．将△ABC沿x轴向右平移，当点C落在直线y=2x﹣6上时，线段BC扫过的面积为（ ）
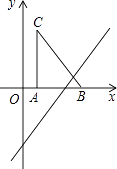A、4 B、8 C、16 D、810. 以x为自变量的二次函数y=x2﹣2（b﹣2）x+b2﹣1的图象不经过第三象限，则实数b的取值范围是（ ）A、b≥ B、b≥1或b≤﹣1 C、b≥2 D、1≤b≤2二、填空题：
-
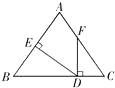
11. 分解因式：8（a2+1）﹣16a= ．12. 若关于x的方程kx2﹣4x﹣1=0有实数根，则k的取值范围是 ．13. 如图，AB=AC，FD⊥BC于D，DE⊥AB于E，若∠AFD=145°，则∠EDF=度．
14. 如图是一个能自由转动的正六边形转盘，这个转盘被三条分割线分成形状相同，面积相等的三部分，且分别标有“1”、“2”、“3”三个数字，指针的位置固定不动，让转盘自由转动两次，当每次转盘停止后，记录指针指向的数（当指针指向分割线时，视其指向分割线左边的区域），则两次指针指向的数都是奇数的概率为 ．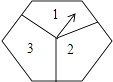
15. 如图，在正方形纸片ABCD中，EF∥AD，M，N是线段EF的六等分点，若把该正方形纸片卷成一个圆柱，使点A与点D重合，此时，底面圆的直径为10cm，则圆柱上M，N两点间的距离是cm．
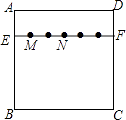16. 二次函数y=ax2+bx的图象如图，若一元二次方程ax2+bx+m=0有实数根，则m的最大值为 ．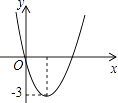
三、计算题
-
17. 计算：﹣14+（2016﹣π）0﹣（﹣）﹣1+|1﹣|﹣2sin60°．18. 先化简再求值： ，其中x满足x2+x﹣2=0．
四、解答题
-
19. 如图，已知PA、PB切⊙O于A，B两点，连AB，且PA，PB的长是方程x2﹣2mx+3=0的两根，AB=m．试求：
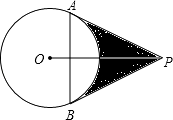(1)、⊙O的半径；(2)、由PA，PB， 围成图形（即阴影部分）的面积．20. 每年11月的最后一个星期四是感恩节，小龙调查了初三年级部分同学在感恩节当天将以何种方式表达感谢帮助过自己的人．他将调查结果分为如下四类：A类﹣﹣当面致谢；B类﹣﹣打电话；C类﹣﹣发短信息或微信；D类﹣﹣写书信．他将调查结果绘制成如图不完整的扇形统计图和条形统计图：请你根据图中提供的信息完成下列各题：
(1)、补全条形统计图；(2)、在A类的同学中，有3人来自同一班级，其中有1人学过主持．现准备从他们3人中随机抽出两位同学主持感恩节主题班会课，请你用树状图或表格求出抽出的两人都没有学过主持的概率．
21. 为方便市民通行，某广场计划对坡角为30°，坡长为60米的斜坡AB进行改造，在斜坡中点D处挖去部分坡体（阴影表示），修建一个平行于水平线CA的平台DE和一条新的斜坡BE．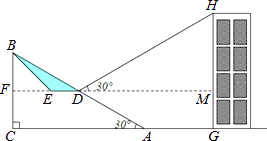
(1)、若修建的斜坡BE的坡角为36°，则平台DE的长约为多少米？(2)、在距离坡角A点27米远的G处是商场主楼，小明在D点测得主楼顶部H 的仰角为30°，那么主楼GH高约为多少米？（结果取整数，参考数据：sin36°=0.6，cos36°=0.8，tan36°=0.7， =1.7）22. 为迎接中国森博会，某商家计划从厂家采购A，B两种产品共20件，产品的采购单价（元/件）是采购数量（件）的一次函数，下表提供了部分采购数据．采购数量（件）
1
2
…
A产品单价（元/件）
1480
1460
…
B产品单价（元/件）
1290
1280
…
(1)、设A产品的采购数量为x（件），采购单价为y1（元/件），求y1与x的关系式；(2)、经商家与厂家协商，采购A产品的数量不少于B产品数量的 ，且A产品采购单价不低于1200元，求该商家共有几种进货方案；
(3)、该商家分别以1760元/件和1700元/件的销售单价售出A，B两种产品，且全部售完，在（2）的条件下，求采购A种产品多少件时总利润最大，并求最大利润．
五、综合题：
-
23. 在△ABC中，AB=AC=5，cos∠ABC=0.6，将△ABC绕点C顺时针旋转，得到△A1B1C．(1)、如图1，当点B1在线段BA延长线上时．①求证：BB1∥CA1；②求△AB1C的面积；
(2)、如图2，点E是BC边的中点，点F为线段AB上的动点，在△ABC绕点C顺时针旋转过程中，点F的对应点是F1 ， 求线段EF1长度的最大值与最小值的差．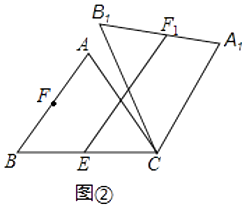
24. 如图，已知抛物线y=ax2+bx+c（a≠0）的顶点坐标为（4，﹣ ），且与y轴交于点C（0，2），与x轴交于A，B两点（点A在点B的左边）．
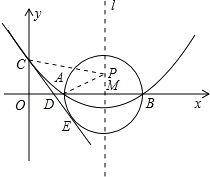(1)、求抛物线的解析式及A、B两点的坐标；
(2)、在（1）中抛物线的对称轴l上是否存在一点P，使AP+CP的值最小？若存在，求AP+CP的最小值，若不存在，请说明理由；
(3)、以AB为直径的⊙M相切于点E，CE交x轴于点D，求直线CE的解析式．