利用勾股定理求线段长度—北师大版数学八(上)知识点训练
试卷更新日期:2024-10-27 类型:复习试卷
一、基础夯实
-
1. 在中,有两边的长分别为1和2,则第三边的长( )A、 B、 C、或 D、或2. 如图,在直角△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段AN的长为
 A、6 B、5 C、4 D、33. 如图,正方形ABCD的面积为15,Rt△BCE的斜边CE的长为8,则BE的长为( )
A、6 B、5 C、4 D、33. 如图,正方形ABCD的面积为15,Rt△BCE的斜边CE的长为8,则BE的长为( ) A、17 B、10 C、6 D、74. 如图,在的正方形网格中,每个小正方形边长为1,点均为格点,以为圆心,长为半径作弧,交网格线于点 , 则两点间的距离为( )
A、17 B、10 C、6 D、74. 如图,在的正方形网格中,每个小正方形边长为1,点均为格点,以为圆心,长为半径作弧,交网格线于点 , 则两点间的距离为( ) A、 B、 C、 D、5. 如图,在三角形纸片中, , 折叠该纸片,使点C落在边上的点处,折痕与交于点 , 若 , 则折痕的长为( )
A、 B、 C、 D、5. 如图,在三角形纸片中, , 折叠该纸片,使点C落在边上的点处,折痕与交于点 , 若 , 则折痕的长为( ) A、3 B、4 C、 D、6. 如图,是一张直角三角形的纸片,两直角边 , 现将折叠,使点B点A重合,折痕为DE,则BD的长为( )
A、3 B、4 C、 D、6. 如图,是一张直角三角形的纸片,两直角边 , 现将折叠,使点B点A重合,折痕为DE,则BD的长为( ) A、7 B、 C、6 D、7. 一等腰三角形的底边长是12,腰长为10,则底边上的高是( )A、15 B、13 C、10 D、88. 如图,在△ABC中,∠C=90°,分别以点A、B为圆心,大于AB长为半径作弧,两弧分别交于M、N两点,过M、N两点的直线交AC于点E,若AC=6,BC=3,则CE的长为( )
A、7 B、 C、6 D、7. 一等腰三角形的底边长是12,腰长为10,则底边上的高是( )A、15 B、13 C、10 D、88. 如图,在△ABC中,∠C=90°,分别以点A、B为圆心,大于AB长为半径作弧,两弧分别交于M、N两点,过M、N两点的直线交AC于点E,若AC=6,BC=3,则CE的长为( ) A、 B、 C、 D、9. 如图,在中, , 是的平分线, , 则的长为( )
A、 B、 C、 D、9. 如图,在中, , 是的平分线, , 则的长为( ) A、6 B、5 C、10 D、810. 如图,在△ABC中,∠C=90°,AC=4cm,BC=3cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CD的长为( )
A、6 B、5 C、10 D、810. 如图,在△ABC中,∠C=90°,AC=4cm,BC=3cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CD的长为( )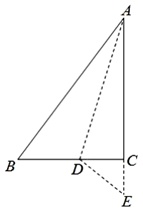 A、1cm B、cm C、cm D、2cm11. 如图,在Rt△ABC中,∠C=90°,AC=8,AB=10,AB的垂直平分线分别交AB、AC于点D、E.求AE的长.
A、1cm B、cm C、cm D、2cm11. 如图,在Rt△ABC中,∠C=90°,AC=8,AB=10,AB的垂直平分线分别交AB、AC于点D、E.求AE的长. 12. 如图,已知中,为的角平分线, , 求的长.
12. 如图,已知中,为的角平分线, , 求的长.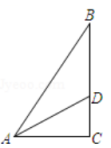 13. 直角三角形纸片的两直角边长分别为6,8,现将 如图折叠,使点A和点B重合,则折痕DE的长是( )
13. 直角三角形纸片的两直角边长分别为6,8,现将 如图折叠,使点A和点B重合,则折痕DE的长是( ) A、3 B、3.5 C、3.75 D、4
A、3 B、3.5 C、3.75 D、4二、能力提升
-
14. 如图,在△ABC中,∠C=90°,以A为圆心,任意长为半径画弧,分别交AC,AB于点M,N,再分别以M,N为圆心,大于MN长为半径画弧,两弧交点O,作射线AO,交BC于点E.已知CE=3,BE=5,则AC的长为( )
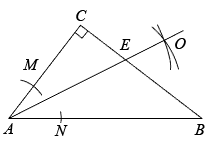 A、8 B、7 C、6 D、515. 如图,在中, , , , 为上一点,将沿折叠,使点恰好落在边上,则折痕的长是( )
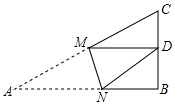
A、8 B、7 C、6 D、515. 如图,在中, , , , 为上一点,将沿折叠,使点恰好落在边上,则折痕的长是( ) A、5 B、 C、 D、16. 如图,在和中, , 点在边的中点上,若 , , 连结 , 则的长为 .
A、5 B、 C、 D、16. 如图,在和中, , 点在边的中点上,若 , , 连结 , 则的长为 .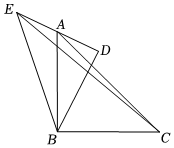 17. 如图,在等腰中, , , O是外一点,O到三边的垂线段分别为 , , , 且 , 则的长度为( )
17. 如图,在等腰中, , , O是外一点,O到三边的垂线段分别为 , , , 且 , 则的长度为( ) A、7 B、5 C、 D、18. 如图,在△ABC中,∠ACB=90°,AC=4,BC=3,D为斜边AB上的一动点(不包含A,B两端点),沿CD折叠,点A落在点A'处,A'C与AB相交于点E若A'D∥BC,则A'E的长为。
A、7 B、5 C、 D、18. 如图,在△ABC中,∠ACB=90°,AC=4,BC=3,D为斜边AB上的一动点(不包含A,B两端点),沿CD折叠,点A落在点A'处,A'C与AB相交于点E若A'D∥BC,则A'E的长为。 19. 如图,在四边形ABCD中,∠A=90°,AD∥BC,AB=4,点P是线段AD上的动点,连接BP,CP,若△BPC周长的最小值为16,则BC的长为.
19. 如图,在四边形ABCD中,∠A=90°,AD∥BC,AB=4,点P是线段AD上的动点,连接BP,CP,若△BPC周长的最小值为16,则BC的长为. 20. 如图所示的正方体木块的棱长为3cm,沿其相邻三个面的对角线(图中虚线)剪掉一角,得到如图②所示的几何体,一只蚂蚁沿着图②中的几何体表面从顶点A爬行到顶点B的最短距离为cm.
20. 如图所示的正方体木块的棱长为3cm,沿其相邻三个面的对角线(图中虚线)剪掉一角,得到如图②所示的几何体,一只蚂蚁沿着图②中的几何体表面从顶点A爬行到顶点B的最短距离为cm.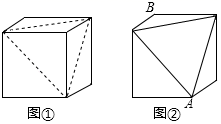 21. 如图,在△ABC中,已知AD是BC边上的高,过点B作BE⊥AC于点E , 交AD于点F , 且AD= , BD= , CD= .
21. 如图,在△ABC中,已知AD是BC边上的高,过点B作BE⊥AC于点E , 交AD于点F , 且AD= , BD= , CD= .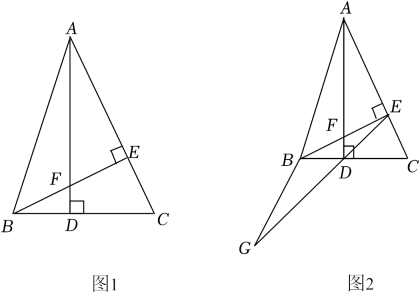 (1)、求BE的长;(2)、求证:AF=BC;(3)、如图2,在(2)的条件下,在ED的延长线上取一点G , 使BG=BE , 请猜想DG与DE的数量关系,并说明理由.
(1)、求BE的长;(2)、求证:AF=BC;(3)、如图2,在(2)的条件下,在ED的延长线上取一点G , 使BG=BE , 请猜想DG与DE的数量关系,并说明理由.三、拓展创新
-
22. 如图,C为线段 上一动点,分别过B,D作 , ,连接 , ,已知 , , ,设 .请用含x的代数式表示 的长为 , 根据上述方法,求出 的最小值为.
 23. [阅读理解]
23. [阅读理解]如图,在△ABC中,AB=4,AC=6,BC=7,过点A作直线BC的垂线,垂足为D,求线段AD的长.

解:设BD=x,则CD=7﹣x.
∵AD⊥BC,
∴∠ADB=∠ADC=90°.
在Rt△ABD中,AD2=AB2﹣BD2 ,
在Rt△ACD中,AD2=AC2﹣CD2 ,
∴AB2﹣BD2=AC2﹣CD2.
又∵AB=4,AC=6,
∴42﹣x2=62﹣(7﹣x)2.
解得x= ,
∴BD= .
∴AD= = .
[知识迁移]
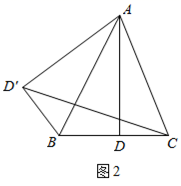
(1)、在△ABC中,AB=13,AC=15,过点A作直线BC的垂线,垂足为D.i)如图1,若BC=14,求线段AD的长;
ii)若AD=12,求线段BC的长.
(2)、如图2,在△ABC中,AB= ,AC= ,过点A作直线BC的垂线,交线段BC于点D,将△ABD沿直线AB翻折后得到对应的△ ,连接CD′,若AD= ,求线段 的长.