黑龙江省哈尔滨市南岗区2017年中考数学模拟试卷(三)
试卷更新日期:2017-12-07 类型:中考模拟
一、选择题
-
1. 实数﹣6的倒数是( )A、﹣ B、 C、﹣6 D、62. 下列计算中正确的是( )A、 + = B、 =3 C、a10=(a5)2 D、b﹣2=﹣b23. 下列图形中,是中心对称图形但不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 用科学记数法表示9 270 000正确的是( )A、9.27×106 B、9.27×105 C、9.27×104 D、927×1035. 不等式组 的解集在数轴上表示为( )A、
4. 用科学记数法表示9 270 000正确的是( )A、9.27×106 B、9.27×105 C、9.27×104 D、927×1035. 不等式组 的解集在数轴上表示为( )A、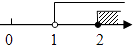 B、
B、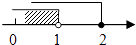 C、
C、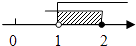 D、
D、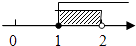 6. 如图,一个几何体由5个大小相同、棱长为1的小正方体搭成,下列关于这个几何体的说法正确的是( )
6. 如图,一个几何体由5个大小相同、棱长为1的小正方体搭成,下列关于这个几何体的说法正确的是( ) A、主视图的面积为5 B、左视图的面积为3 C、俯视图的面积为3 D、三种视图的面积都是47. 将抛物线y=x2向左平移2个单位,再向下平移3个单位,则得到的抛物线解析式是( )A、y=(x﹣2)2﹣3 B、y=(x﹣2)2+3 C、y=(x+2)2﹣3 D、y=(x+2)2+38. 如图,AB为⊙O的直径,弦CD⊥AB于点E,若AE=8,BE=2,则CD=( )
A、主视图的面积为5 B、左视图的面积为3 C、俯视图的面积为3 D、三种视图的面积都是47. 将抛物线y=x2向左平移2个单位,再向下平移3个单位,则得到的抛物线解析式是( )A、y=(x﹣2)2﹣3 B、y=(x﹣2)2+3 C、y=(x+2)2﹣3 D、y=(x+2)2+38. 如图,AB为⊙O的直径,弦CD⊥AB于点E,若AE=8,BE=2,则CD=( ) A、5 B、8 C、2 D、49. 如图,在△ABC中,AB=AC=5,BC=6,点M为BC的中点,MN⊥AC于点N,则MN等于( )
A、5 B、8 C、2 D、49. 如图,在△ABC中,AB=AC=5,BC=6,点M为BC的中点,MN⊥AC于点N,则MN等于( )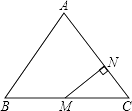 A、 B、 C、 D、10. 甲、乙两车从同地沿同一路线去600km外的某地取货,甲比乙先出发,他们去时所走的路程S(km)与时间t(h)之间的函数图象如图所示,则以下说法中正确的有( )
A、 B、 C、 D、10. 甲、乙两车从同地沿同一路线去600km外的某地取货,甲比乙先出发,他们去时所走的路程S(km)与时间t(h)之间的函数图象如图所示,则以下说法中正确的有( )①甲比乙早出发8h;
②相遇前,乙的速度是甲的速度的5倍;
③相遇后甲提速了,乙降速了;
④乙出发2h后追上甲;
⑤甲比原计划(按初始速度行驶)晚到目的地4h.
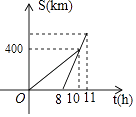 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 化简:﹣= .12. 函数y= 中自变量x的取值范围是 .13. 分解因式:ax2﹣2ax+a= .14. 在等腰三角形ABC中,∠C=90°,BC=2cm,如果以AC的中点O为旋转中心,将△ABC旋转180°,点B落在B′处,则BB′的长度为 .15. 某工厂原计划生产7200顶帐篷,后来有一个地区突然发生地震,要求工厂生产的帐篷比原计划多20%,并且需提前4天完成任务.已知实际生产时每天比原计划多生产720顶帐篷,设实际每天生产x顶帐篷,根据题意可列方程为 .
16. 在一个不透明的袋子里,有5个除颜色外,其他都相同的小球,其中有3个是红球,2个是绿球,每次拿一个球然后放回去,拿2次,则至少有一次取到绿球的概率是 .17. 如图,反比例函数y= (k>0)的图象与以原点(0,0)为圆心的圆交于A,B两点,且A(1, ),图中阴影部分的面积等于 . (结果保留π) 18. 如图,AB是⊙O的直径,AC是⊙O的切线,连接OC与⊙O相交于点D,连接BD,∠C=40°,若点P为优弧 上的动点,连接PA、PD,则∠APD的大小是度.
18. 如图,AB是⊙O的直径,AC是⊙O的切线,连接OC与⊙O相交于点D,连接BD,∠C=40°,若点P为优弧 上的动点,连接PA、PD,则∠APD的大小是度. 19. 如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向向右平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于 .
19. 如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向向右平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于 . 20. 已知点F是等边△ABC边CA延长线上一点,点D是线段BF上一点,且BC=CD,CD交AB于点E,若AE=6,CE=14,则AF= .
20. 已知点F是等边△ABC边CA延长线上一点,点D是线段BF上一点,且BC=CD,CD交AB于点E,若AE=6,CE=14,则AF= .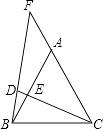
三、解答题
-
21. 先化简,再求代数式(1﹣ )÷ 的值,其中x=4sin45°﹣2cos60°.
22. 图1、图2分别是10×6的网格,网格中每个小正方形的边长均为1,每个网格中画有一个平行四边形,请分别在图1、图2中各画一条线段,各图均满足以下要求:
线段的一个端点为平行四边形的顶点,另一个端点在平行四边形一边的格点上(每个小正方形的顶点均为格点);
将平行四边形分割成两个图形,图1、图2中的分法各不相同,但都要求其中一个是轴对称图形.
23. 某市少年宫准备组织市区部分学校的中小学生到本市A,B,C,D,E五个旅游景区“一日游”,每名学生只能在五个景区中任选一个,为估算到各景区“一日游”的学生人数,少年宫随机抽取这些学校的部分学生,进行了“五个景区你最想去那里”的问卷调查,并把统计结果绘制成如图所示的统计图.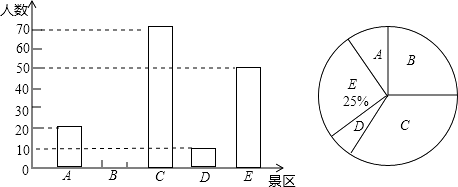 (1)、求参加问卷调查的学生数,并将条形统计图补充完整;(2)、若参加“一日游”的学生为1000人,请估计到C景区“一日游”的学生人数.24. 已知四边形ABCD是正方形,点E、F分别在边AB、边BC上,DE⊥AF,DE与AF交于点O,将线段AE沿AF进行平移至FG,过点G作GH⊥AB的延长线于点H.
(1)、求参加问卷调查的学生数,并将条形统计图补充完整;(2)、若参加“一日游”的学生为1000人,请估计到C景区“一日游”的学生人数.24. 已知四边形ABCD是正方形,点E、F分别在边AB、边BC上,DE⊥AF,DE与AF交于点O,将线段AE沿AF进行平移至FG,过点G作GH⊥AB的延长线于点H.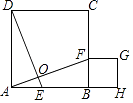 (1)、判断四边形BFGH的形状并证明;(2)、写出图中所有面积相等的图形.25. 在春节来临之际,小杨的服装小店用2500元购进了一批时尚围巾,上市后很快售完,小杨又用8400元购进第二批这种围巾,所购数量是第一批购进数量的3倍,但每条围巾的进价多了3元.(1)、小杨两次共购进这种围巾多少条?(2)、如果这两批围巾每条的售价相同,且全部售完后总利润率不低于20%,那么每条围巾的售价至少是多少元?
(1)、判断四边形BFGH的形状并证明;(2)、写出图中所有面积相等的图形.25. 在春节来临之际,小杨的服装小店用2500元购进了一批时尚围巾,上市后很快售完,小杨又用8400元购进第二批这种围巾,所购数量是第一批购进数量的3倍,但每条围巾的进价多了3元.(1)、小杨两次共购进这种围巾多少条?(2)、如果这两批围巾每条的售价相同,且全部售完后总利润率不低于20%,那么每条围巾的售价至少是多少元?
26. 如图1,等边△ABC为⊙O的内接三角形,点G和点F在⊙O上且位于点A的两侧,连接BF、CG交于点E,且BF=CG. (1)、求证:∠BEC=120°;(2)、如图2,取BC边中点D,连接AE、DE,求证:AE=2DE;(3)、如图3,在(2)的条件下,过点A作⊙O的切线交BF的延长线于点H,若AE=AH=4,请求出⊙O的半径长.27. 如图1,在平面直角坐标系中,O为坐标原点,抛物线y=a(x﹣h)2﹣4(a>0)与x轴分别交于原点O、A两点,点A在x轴的正半轴上,顶点为D,直线y= x交抛物线于B点,过B作BE∥x轴交抛物线另一点E,交对称轴于F.
(1)、求证:∠BEC=120°;(2)、如图2,取BC边中点D,连接AE、DE,求证:AE=2DE;(3)、如图3,在(2)的条件下,过点A作⊙O的切线交BF的延长线于点H,若AE=AH=4,请求出⊙O的半径长.27. 如图1,在平面直角坐标系中,O为坐标原点,抛物线y=a(x﹣h)2﹣4(a>0)与x轴分别交于原点O、A两点,点A在x轴的正半轴上,顶点为D,直线y= x交抛物线于B点,过B作BE∥x轴交抛物线另一点E,交对称轴于F. (1)、当DF=4a时,求BE的长.(2)、如图2,连AD,连接AD绕点A旋转交直线OB于点G,点D的对应点为G,当OG=2时,求a的值;
(1)、当DF=4a时,求BE的长.(2)、如图2,连AD,连接AD绕点A旋转交直线OB于点G,点D的对应点为G,当OG=2时,求a的值;
(3)、在(2)的条件下,当0<a<1时,以OB为直径作圆交x轴下方抛物线于点P,求点P坐标.