黑龙江省哈尔滨六十九中2017年中考数学一模试卷
试卷更新日期：2017-12-07 类型：中考模拟
一、选择题
-
1. 我市4月份某天的最高气温是22℃，最低气温是8℃，那么这天的温差是（ ）A、30℃ B、14℃ C、﹣14℃ D、12℃2. 下列运算正确的是（ ）A、a+a=a2 B、a2•a=a2 C、a3÷a2=a （a≠0） D、（a2）3=a53. 下面四个图形中，不是中心对称图形的是（ ）A、
B、
C、
D、
4. 如图是由四个完全相同的正方体组成的几何体，这个几何体的左视图是（ ）
A、
B、
C、
D、
5. 若反比例函数y=的图象经过点（2，﹣1），则该反比例函数的图象在（ ）A、第一、二象限 B、第一、三象限 C、第二、三象限 D、第二、四象限6. 如图，四边形ABCD内接于⊙O，若∠BOD=138°，则它的一个外角∠DCE等于（ ）
A、69° B、42° C、48° D、38°7. 如图，在△ABC中，∠CAB=70°，将△ABC绕点A按逆时针方向旋转一个锐角α到△AB′C′的位置，连接CC′，若CC′∥AB，则旋转角α的度数为（ ）
A、40° B、50° C、30° D、35°8. 如图，点A为∠α边上的任意一点，作AC⊥BC于点C，CD⊥AB于点D，下列用线段比表示cosα的值，错误的是（ ）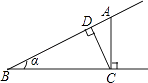
A、 B、 C、 D、9. 下列说法中正确的是（ ）A、不在同一条直线上的三个点确定一个圆 B、相等的圆心角所对的弧相等 C、平分弦的直径垂直于弦 D、在同圆或等圆中，相等的弦所对的圆周角相等10. 已知A、B两地相距4km，上午8：00时，亮亮从A地步行到B地，8：20时芳芳从B地出发骑自行车到A地，亮亮和芳芳两人离A地的距离S（km）与亮亮所用时间t（min）之间的函数关系如图所示，芳芳到达A地时间为（ ）
A、8：30 B、8：35 C、8：40 D、8：45二、填空题
-
11. 长城某段长约为690 000米，690 000用科学记数法表示为 ．
12. 在函数y= 中，自变量x的取值范围是 ．13.
不等式组 的解集是 ．
14. 代数式ax2﹣4ax+4a分解因式，结果是 ．15. 现有四个外观完全一样的粽子，其中有且只有一个有蛋黄．若从中一次随机取出两个，则这两个粽子都没有蛋黄的概率是 ．16. 已知扇形的半径为5cm，圆心角等于120°，则该扇形的弧长等于 ．17. 某商品经过两次连续的降价，由原来的每件25元降为每件16元，则该商品平均每次降价的百分率为 ．18. 如图，已知P为⊙O内一点，且OP=2cm，如果⊙O的半径是3cm，那么过P点的最短的弦等于 cm．
19. 已知△ABC，O为AC中点，点P在AC上，若OP= ，tan∠A= ，∠B=120°，BC=2 ，则AP= ．20. 已知正方形ABCD的边长为4，点E，F分别在边BC、CD上，∠EAF=45°，若AE•AF= ，则EF的长为 ．
三、解答题
-
21. 化简求值：（ ﹣1）÷ ，其中x=tan60°﹣1．22. 图a、图b是两张形状、大小完全相同的方格纸，方格纸中每个小正方形的边长均为1，点A、B在小正方形的顶点上．
(1)、在图a中画出△ABC（点C在小正方形的顶点上），使△ABC是等腰三角形且△ABC为钝角三角形；(2)、在图b中画出△ABD（点D在小正方形的顶点上），使△ABD是等腰三角形，且tan∠ABD=1．23. 某学校为了解学生的课外阅读情况，王老师随机抽查部分学生，并对其暑假期间的课外阅读量进行统计分析，绘制成如图所示但不完整的统计图．已知抽查的学生在暑假期间阅读量为2本的人数占抽查总人数的20%，根据所给出信息，解答下列问题：
(1)、求被抽查学生人数并直接写出被抽查学生课外阅读量的中位数；(2)、将条形统计图补充完整；(3)、若规定：假期阅读3本及3本以上课外书者为完成假期作业，据此估计该校1500名学生中，完成假期作业的有多少名学生？24. 已知菱形ABCD的对角线相交于O，点E，F分别在边AB、BC上，且BE=BF，射线EO，FO分别交边CD、AD于G，H．
(1)、求证：四边形EFGH为矩形；(2)、若OA=4，OB=3，求EG的最小值．25. 某商品经销店欲购进A、B两种纪念品，用160元购进的A种纪念品与用240元购进的B种纪念品的数量相同，每件B种纪念品的进价比A种纪念品的进价贵10元．
(1)、求A、B两种纪念品每件的进价分别为多少元？
(2)、若该商店A种纪念品每件售价24元，B种纪念品每件售价35元，这两种纪念品共购进1 000件，这两种纪念品全部售出后总获利不低于4 900元，求A种纪念品最多购进多少件．
26. 已知AB为⊙O的直径，CD为⊙O的弦，CD∥AB，过点B的切线与射线AD交于点M，连接AC，BD．
(1)、如图l，求证：AC=BD；(2)、如图2，延长AC、BD交于点F，作直径DE，连接AE、CE，CE与AB交于点N，求证：∠AFB=2∠AEN；(3)、如图3，在（2）的条件下，过点M作MQ⊥AF于点Q，若MQ：QC=3：2，NE=2，求QF的长．27. 已知：如图，抛物线y=﹣ （x﹣h）2+k与x轴交于A、B，与y轴交于C，抛物线的顶点为D，对称轴交x轴于H，直线y= x+ 经过点A与对称轴交于E，点E的纵坐标为3．
(1)、求h、k的值；(2)、点P为第四象限抛物线上一点，连接PH，点Q为PH的中点，连接AQ、AP，设点P的横坐标为t，△AQP的面积为S，求S与t的函数关系式（直接写出自变量t的取值范围）；
(3)、在（2）的条件下，过点Q作y轴的平行线QK，过点D作y轴的垂直DK，直线QK、DK交于点K，连接PK、EK，若2∠DKE+∠HPK=90°，求点P的横坐标．