蚂蚁爬行模型—北师大版数学八（上）知识点训练
试卷更新日期：2024-10-27 类型：复习试卷
一、选择题
-
1.
如图，一圆柱高8cm，底面半径为cm，一只蚂蚁从点A爬到点B处吃食，要爬行的最短路程是（ ）
A、12cm B、10cm C、8cm D、6cm2. 如图，已知圆柱的底面直径BC= ，高AB=3，小虫在圆柱表面爬行，从C点爬到A点，然后再沿另一面爬回C点，则小虫爬行的最短路程为（ ）
A、 B、 C、 D、3. 如图，圆柱形玻璃杯高为11cm，底面周长为30cm，在杯内壁离杯底5cm的点B处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿2cm与蜂蜜相对的点A处，则蚂蚁从外壁A处爬行到内壁B处的最短路线长为(杯壁厚度不计)（ ）
A、12cm B、17cm C、20cm D、25cm4. 如图，正方体的棱长为6cm，A是正方体的一个顶点，B是侧面正方形对角线的交点，一只蚂蚁在正方体的表面上爬行，从点A爬到点B的最短路径长是（ ）
A、12cm B、(+6)cm C、cm D、9cm5. 如图，一个棱长为3的正方体，把它分成 个小正方体，小正方体的棱长都是1.如果一只蚂蚁从点A爬到点B，那么估计A，B间的最短路程d的值为（ ）
A、4 B、5 C、6 D、76. 有一长、宽、高分别为 ， ， 的长方体木块，一只蚂蚁沿如图所示路径从顶点 处在长方体的表面爬到长方体上和 相对的中点 处，则需要爬行的最短路径长为（ ）
A、 B、 C、 D、7. 如图，长方体的高为9dm，底面是边长为6dm的正方形，如果一只蚂蚁从顶点A开始爬向顶点B，那么它爬行的最短路程为（ ）
A、10dm B、12dm C、13dm D、15dm8.如图所示，正方体的顶点P处放了一点糖，四只蚂蚁从同一顶点A处分别沿表面不同的路线爬向P处，则所爬行的路程最短的是（ ）
A、甲 B、乙 C、丙 D、丁二、填空题
-
9. 有一个如图所示的长方体透明玻璃鱼缸，假设其长 ，高 ，水深为 ，在水面上紧贴内壁 处有一鱼饵， 在水面线 上，且 ．一小虫想从鱼缸外的 点沿壁爬进鱼缸内 处吃鱼饵，则小虫爬行的最短路线长为 ．
10. 如图，长方体的底面边长分别为和 ， 高为 ， 如果一只蚂蚁从点开始经过四个侧面爬行一圈到达点 ， 那么蚂蚁爬行的最短路径长为 ．
11. 如图，一个三级台阶，它的每一级的长宽和高分别为20、3、2，A和B是这个台阶两个相对的端点，A点有一只蚂蚁，想到B点去吃可口的食物，则蚂蚁沿着台阶面爬到B点最短路程是
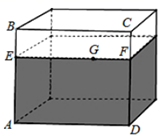
12. 如图，教室的墙面ADEF与地面ABCD垂直，点P在墙面上．若PA＝AB＝5米，点P到AD的距离是3米，有一只蚂蚁要从点P爬到点B ， 它的最短行程是米．
13. 棱长分别为3 cm和2 cm的两个正方体如图所示放置，点A，B，E在同一直线上，顶点G在棱BC上，点P是棱E1F1的中点.一只蚂蚁要沿着正方体的表面从点A爬到点P，它爬行的最短距离是.
14. 在一个长为2米，宽为1米的长方形草地上，如图堆放着一根正三棱柱的木块，它的侧棱长平行且大于场地宽AD，木块的主视图是边长为0.4米的正三角形，一只蚂蚁从点A处到C处需要走的最短路程是 米．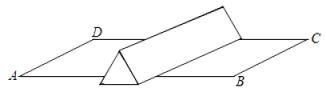
三、解答题
-
15. 有一个如图所示的长方体透明玻璃鱼缸，其长AD= 80 cm，高AB=60 cm，水深AE=40 cm，在水面上紧贴内壁G处有一鱼饵，G在水面线EF上，且EG=60cm．一小虫想从鱼缸外的A点沿壁爬进鱼缸内G处吃鱼饵．
(1)、小虫应该走怎样的路线才能使爬行的路线最短呢？请你在图中画出它爬行的路线，并用箭头标注．(2)、求小虫爬行的最短路线长．16. 如图，只蚂蚁要从正方体纸箱的一个顶点A沿表面爬行到顶点P。
(1)、画出正方体的一种展开图。(可适当调整大小。)(2)、在展开图上画出蚂蚁爬行的最短路线。(3)、在原纸箱图上画出蚂蚁爬行的最短路线。17. 如图1，一只蚂蚁要从圆柱的下底面的点爬到上底面的点处，求它爬行的最短距离．已知圆柱底面半径为 ， 高度为 ． 小明同学在研究这个问题时，提出了两种可供选择的方案，方案1：沿爬行；方案2：沿圆柱侧面展开图的线段爬行，如图2．（取3）图1
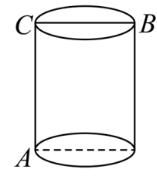图2
(1)、当 ， 时，哪种方式的爬行距离更近？(2)、当 ， 时，哪种方式的爬行距离更近？(3)、当与满足什么条件时，两种方式的爬行距离同样远？18. 课本再现如图1，有一个圆柱，它的高为12cm，底面圆的周长为18cm．在圆柱下底面的点A处有一只蚂蚁，它想吃到上底面与点A相对的点B处的食物，蚂蚁沿圆柱侧面爬行的最短路程是多少？
(1)、方法探究对于立体图形中求最短路程问题，应把立体图形展开成平面图形，再确定A ， B两点的位置，依据“两点之间线段最短”，结合勾股定理，解决相应的问题．如图2，在圆柱的侧面展开图中，点A ， B对应的位置如图所示，利用勾股定理求出蚂蚁爬行的最短路程是cm．
(2)、方法应用如图3，直四棱柱的上下底面是正方形，底面边长为3cm，高为10cm．在其侧面从点A开始，绕侧面两周，嵌入装饰彩条至点B停止．求彩条的最短长度．
(3)、如图4，圆柱形玻璃杯底面周长为30cm，高为35 cm，杯底厚1cm．在玻璃杯外壁距杯口2cm的点A处有一只蚂蚁，蚂蚁相对面的内壁底部B处有一滴蜂蜜，蚂蚁沿杯口爬入内壁去吃蜂蜜，求蚂蚁爬行的最短路径长．（玻璃杯的壁厚忽略不计）
19. 如图，是一个圆柱形的饼干盒，在盒子外侧下底面的点A处有甲、乙两只蚂蚁，它们都想要吃到上底面外侧B′处的食物：甲蚂蚁沿A→A′→B′的折线爬行，乙蚂蚁沿圆柱的侧面爬行：若∠AOB=∠A′O′B′=90°（AA′、BB′都与圆柱的中轴线OO′平行），圆柱的底面半径是12cm，高为1cm，则：
(1)、A′B′=cm，甲蚂蚁要吃到食物需爬行的路程长l1=cm；(2)、乙蚂蚁要吃到食物需爬行的最短路程长l2=cm（π取3）；(3)、若两只蚂蚁同时出发，且爬行速度相同，在乙蚂蚁采取最佳策略的前提下，哪只蚂蚁先到达食物处？请你通过计算或合理的估算说明理由．（参考数据：π取3， ≈1.4）