广西崇左市天等县2017年中考数学一模试卷

试卷更新日期：2017-12-07 类型：中考模拟

进入出卷网下载

一、选择题

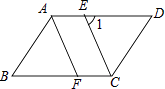
1. 实数0是（）

A、有理数 B、无理数 C、正数 D、负数

查看试题解析
2. 某市今年参加中考的学生人数大约为2.08×10⁴人，对于这个用科学记数表示的近似数，下列说法中正确的是（）

A、精确到百分位 B、精确到十分位 C、精确到个位 D、精确到百位

查看试题解析
3. 如图所示，AB∥CD，EF，HG相交于点O，∠1=40°，∠2=60°，则∠EOH的角度为（）

A、80° B、100° C、140° D、120°

查看试题解析
4. 如图所示，给出下列条件：①∠B=∠ACD；②∠ADC=∠ACB；③ $\frac{A C}{C D} = \frac{A B}{B C}$ ；④AC²=AD•AB．其中单独能够判定△ABC∽△ACD的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
5. 下列几何体的三视图相同的是（）

A、圆柱 B、球 C、圆锥 D、长方体

查看试题解析
6. 下列计算正确的是（）

A、ab•ab=2ab B、（2a）³=2a³ C、3 $\sqrt{a}$ ﹣ $\sqrt{a}$ =3（a≥0） D、 $\sqrt{a}$ • $\sqrt{b}$ = $\sqrt{a b}$ （a≥0，b≥0）

查看试题解析
7. 如图，小贤为了体验四边形的不稳定性，将四根木条用钉子钉成一个矩形框架ABCD ， B与D两点之间用一根橡皮筋拉直固定，然后向右扭动框架，观察所得四边形的变化，下列判断错误的是（　　）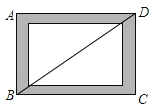

A、四边形ABCD由矩形变为平行四边形 B、BD的长度增大 C、四边形ABCD的面积不变 D、四边形ABCD的周长不变

查看试题解析
8. 如图，已知在⊙O中，AB是弦，半径OC⊥AB，垂足为点D，要使四边形OACB为菱形，还需要添加一个条件，这个条件可以是（）

A、AD=BD B、OD=CD C、∠CAD=∠CBD D、∠OCA=∠OCB

查看试题解析
9. 若反比例函数y= $\frac{k}{x}$ 的图象经过点（2，3），则它的图象也一定经过的点是（）

A、（﹣3，﹣2） B、（2，﹣3） C、（3，﹣2） D、（﹣2，3）

查看试题解析
10. 关于x的一元二次方程x²﹣6x+2k=0有两个不相等的实数根，则实数k的取值范围是（）

A、 $k \leq \frac{9}{2}$ B、 $k < \frac{9}{2}$ C、 $k \geq \frac{9}{2}$ D、 $k > \frac{9}{2}$

查看试题解析
11. 在一个不透明的盒子中装有3个红球、2个黄球和1个绿球，这些球除了颜色外无其他差别．从中随机摸出一个小球，恰好是黄球的概率为（　　）

A、 $\frac{1}{6}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{2}{3}$

查看试题解析
12. 观察下列各式及其展开式：
（a+b）²=a²+2ab+b²
（a+b）³=a³+3a²b+3ab²+b³
（a+b）⁴=a⁴+4a³b+6a²b²+4ab³+b⁴
（a+b）⁵=a⁵+5a⁴b+10a³b²+10a²b³+5ab⁴+b⁵
…
请你猜想（a+b）¹⁰的展开式第三项的系数是（）

A、36 B、45 C、55 D、66

查看试题解析

二、填空题

13. 分解因式：2a²﹣8= ．

查看试题解析
14. 九年级某班40位同学的年龄如表所示：
年龄（岁）
13
14
15
16
人数
3
16
19
2
则该班40名同学年龄的众数和中位数分别是．

查看试题解析
15. 如图，⊙O的直径AB过弦CD的中点E，若∠C=25°，则∠D= ．

查看试题解析
16. 如图，以O为位似中心将四边形ABCD放大后得到四边形A′B′C′D′，若OA=4，OA′=8，则四边形ABCD和四边形A′B′C′D′的周长的比为．

查看试题解析
17.
如图，Rt△ABC中∠A=90°，∠C=30°，BD平分∠ABC且与AC边交于点D，AD=2，则点D到边BC的距离是．

查看试题解析
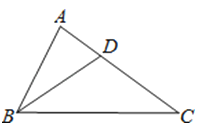18. 如图为二次函数y=ax²+bx+c的图象，在下列说法中：
①ac＜0；
②方程ax²+bx+c=0的根是x₁=﹣1，x₂=3；
③a+b+c＞0；
④当x＞1时，y随着x的增大而增大．
正确的说法有．（请写出所有正确的序号）

查看试题解析

三、解答题

19. 计算：|﹣3|+（ $\sqrt{3}$ ﹣π）⁰﹣2tan45°．

查看试题解析
20. 求不等式组 ${\begin{matrix} 2 x + 1 > 0 ① \\ x > 2 x - 5 ② \end{matrix}$ 的正整数解．

查看试题解析
21. 如图，在6×8的网格中，每个小正方形的边长均为1，点O和△ABC的顶点均为小正方形的顶点．

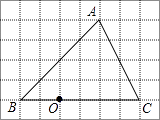(1)、在图中△ABC的内部作△A′B′C′，使△A′B′C′和△ABC位似，且位似中心为点O，位似比为1：2；

(2)、连接（1）中的AA′，则线段AA′的长度是．

查看试题解析
22. 为加强学生身体锻炼，某校开展体育“大课间”活动，学校决定在学生中开设A：篮球，B：立定跳远，C：跳绳，D：跑步，E：排球五种活动项目．为了了解学生对五种项目的喜欢情况，随机抽取了部分学生进行调查，并将调查结果绘制成如图所示的两个统计图．请结合图中的信息解答下列问题：

(1)、在这项调查中，共调查了名学生；

(2)、请将两个统计图补充完整；

(3)、若该校有1200名在校学生，请估计喜欢排球的学生大约有多少人？

查看试题解析
23. 如图，AB是⊙O的弦，OP⊥OA交AB于点P，过点B的直线交OP的延长线于点C，且CP=CB．

(1)、求证：BC是⊙O的切线；

(2)、若⊙O的半径为 $\sqrt{5}$ ，OP=1，求BC的长．

查看试题解析
24. 为响应区“美丽广西　清洁乡村”的号召，某校开展“美丽广西　清洁校园”的活动，该校经过精心设计，计算出需要绿化的面积为498m² ，绿化150m²后，为了更快的完成该项绿化工作，将每天的工作量提高为原来的1.2倍．结果一共用20天完成了该项绿化工作．该项绿化工作原计划每天完成多少m²？

查看试题解析
25. 已知平行四边形ABCD中，CE平分∠BCD且交AD于点E，AF∥CE，且交BC于点F．

(1)、求证：△ABF≌△CDE；

(2)、如图，若∠1=65°，求∠B的大小．

查看试题解析
26. 如图，抛物线y=ax²+bx+c（a≠0）与x轴交于A（﹣4，0），B（2，0），与y轴交于点C（0，2）．

(1)、求抛物线的解析式；

(2)、若点D为该抛物线上的一个动点，且在直线AC上方，当以A、C、D为顶点的三角形面积最大时，求点D的坐标及此时三角形的面积；

(3)、以AB为直径作⊙M，直线经过点E（﹣1，﹣5），并且与⊙M相切，求该直线的解析式．

查看试题解析

年龄（岁）	13	14	15	16
人数	3	16	19	2