勾股定理的实际应用—北师大版数学八（上）知识点训练

试卷更新日期：2024-10-27 类型：复习试卷

进入出卷网下载

一、基础夯实

1. 如图，一个工人拿一个2.5米长的梯子，底端A放在距离墙根C点0.7米处，另一头B点靠墙，如果梯子的顶部下滑0.4米，梯子的底部向外滑多少米？（）

A、0.4 B、0.6 C、0.7 D、0.8

查看试题解析
2. 小明想知道学校旗杆的高度，他发现旗杆上的绳子垂到地面还多 $1$ 米，当他把绳子的下端拉开 $5$ 米后，发现下端刚好接触地面，则旗杆的高是（）

A、 $8$ 米 B、 $10$ 米 C、 $12$ 米 D、 $13$ 米

查看试题解析
3. 一根旗杆在离地面3米处断裂，旗杆顶部落在离旗杆底部4米处，旗杆折断之前的高度是（）

A、5米 B、7米 C、8米 D、9米

查看试题解析
4. 如图，有一个正方体盒子，棱长为 $1 cm$ ，一只蚂蚁从盒底点A沿盒的表面爬到盒顶的点B，蚂蚁爬行的最短路程是（）

A、 $\sqrt{5} cm$ B、 $3 cm$ C、 $\sqrt{3} cm$ D、 $2 cm$

查看试题解析
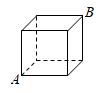5. 如图所示，长为8 cm的橡皮筋放置在x轴上，固定两端A和B，然后把中点C向上拉升3 cm至D点，则橡皮筋被拉长了(　　)

A、2 cm B、3 cm C、4 cm D、5 cm

查看试题解析
6. 小华新买了一条跳绳，如图1，他按照体育老师教的方法确定适合自己的绳长：一脚踩住绳子的中央，手肘靠近身体，两肘弯屈 $9 0^{∘}$ ，小臂水平转向两侧，两手将绳拉直，绳长即合适长度。将图1抽象成如图2，若两手握住的绳柄两端距离约为1米，小臂到地面的距离约1. 2米，则适合小华的绳长为（）

A、2. 2米 B、2. 4米 C、2. 6米 D、2. 8米

查看试题解析
7. 如图，秋千静止时，踏板离地的垂直高度 $B E = 1 m$ ，将它往前推 $6 m$ 至 $C$ 处时 $（$ 即水平距离 $C D = 6 m ）$ ，踏板离地的垂直高度 $C F = 4 m$ ，它的绳索始终拉直，则绳索 $A C$ 的长是（）

A、 $\frac{21}{2} m$ B、 $\frac{15}{2} m$ C、 $6 m$ D、 $\frac{9}{2} m$

查看试题解析
8. 如图，将一根长12厘米的筷子置于底面直径为6厘米，高为8厘米的圆柱形杯子中，则筷子露在杯子外面的长度至少为厘米.

查看试题解析
9. 如图，学校有一块长方形花圃，有极少数人为了避开拐角走“捷径”，在花圃内走出了一条“路”．他们仅仅少走了m路，却踩伤了花草

查看试题解析
10. 《九章算术》中的“折竹抵地”问题：今有竹高一丈，末折抵地，去根六尺．问折高者几何？意思是：一根竹子，原高一丈(一丈＝10尺)，一阵风将竹子折断，其竹梢恰好抵地，抵地处离竹子底部6尺远，问折断处离地面的高度是多少？设折断处离地面的高度为x尺，则可列方程为．

查看试题解析
11. 在我国古代数学著作《九章算术》中记载了一个有趣的问题，这个问题的意思是：有一个水池，水面是一个边长为10尺的正方形，在水池正中央有一根新生的芦苇，它高出水面1尺，如图所示，如果把这根芦苇垂直拉向岸边，它的顶端恰好到达岸边的水面．那么水深多少？芦苇长为多少？

查看试题解析
12. 如图，一辆小汽车在一段限速 $110 k m / h$ 高速公路上沿直道行驶，某一时刻刚好行驶到路对面车速检测仪 $A$ 的正前方 $80 m$ 的 $C$ 处，过了 $2 s$ 后，测得小汽车到达与车速检测仪 $A$ 之间的距离为 $100 m$ 的 $B$ 处．

(1)、你能计算这辆小汽车的速度吗？

(2)、这辆小汽车超速了吗？

查看试题解析
13. 如图，某住宅社区在相邻两楼之间修建一个上方是以AB为直径的半圆，下方是长方形的仿古通道，已知AD＝2.3米，CD＝2米；现有一辆卡车装满家具后，高2.5米，宽1.6米，请问这辆送家具的卡车能否通过这个通道？请说出你的理由．

查看试题解析
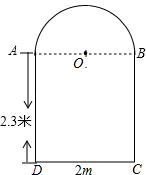14. 综合与实践：测雕塑

(1)、如图，雕塑底座正面是四边形ABCD ，现提供一足够长的卷尺，请你设计一个方法检测雕塑底座正面的边AB是否垂直于底边BC？并说明理由.

(2)、若雕塑底座是个长方体，量得边BC长50cm，边CD长40cm，边DE长30cm，一只蚂蚁从底部点B沿雕塑的表面爬到顶部的点E ，蚂蚁爬行的最短路程是多少？

查看试题解析
15. 风筝是由中国古代劳动人民发明于春秋时期，至今已有2000多年的历史，北宋张择端的《清明上河图》，苏汉臣的《百子图》里都有放风筝的生动景象．某校八年级五班的实践探究小组的同学学习了“勾股定理”之后，在放风筝时想测量风筝离地面的垂直高度CE（如图，线段AE表示水平地面），他们进行了如下操作：①测得水平距离 $B D$ 的长为15米；②已经放出的风筝线 $B C$ 的长为39米（其中风筝本身的长宽忽略不计）；③牵线放风筝的小辉同学的身高为1.7米．

(1)、求风筝的垂直高度 $C E$ ；

(2)、如果实践探究小组的同学想让风筝沿 $C D$ 方向下降到距地面21.7米，则小辉同学应该往回收线多少米？

查看试题解析

二、能力提升

16. 如图，一个长方体形盒子的长、宽、高分别为 $5$ 厘米、 $3$ 厘米、 $10$ 厘米，在长方体一底面的顶点 $A$ 有一只蚂蚁，它想吃点 $B$ 处的食物，沿长方体侧面爬行的最短路程是（）

A、 $13$ 厘米 B、 $2 \sqrt{41}$ 厘米 C、 $3 \sqrt{26}$ 厘米 D、 $\sqrt{194}$ 厘米

查看试题解析
17. 如图，透明的圆柱形容器（容器厚度忽略不计）的高为 $12 cm$ ，底面周长为 $16 cm$ ，在容器内壁离容器底部 $3 cm$ 的点B处有一饭粒，此时一只蚂蚁正好在容器外壁，且离容器上沿 $3 cm$ 的点A处，则蚂蚁吃到饭粒需爬行的最短路径为 $cm$ ．

查看试题解析
18. 如图，圆柱底面半径为 $\frac{4}{π} c m$ ，高为 $18 c m$ ，点 $A$ 、 $B$ 分别是圆柱两底面圆周上的点，且 $A$ 、 $B$ 在同一母线上，用一根棉线从 $A$ 点顺着圆柱侧面绕 $3$ 圈到 $B$ 点，则这根棉线的长度最短为（）

A、 $24 c m$ B、 $30 c m$ C、 $2 \sqrt{21} c m$ D、 $4 \sqrt{97} c m$

查看试题解析
19. 如图是学校艺术馆中的柱子，高4.5m ．为迎接艺术节的到来，工作人员用一条花带从柱底向柱顶均匀地缠绕3圈，一直缠到起点的正上方为止．若柱子的底面周长是2m ，则这条花带至少需要m ．

查看试题解析

20. 课本再现

如图1，有一个圆柱，它的高为12cm，底面圆的周长为18cm．在圆柱下底面的点A处有一只蚂蚁，它想吃到上底面与点A相对的点B处的食物，蚂蚁沿圆柱侧面爬行的最短路程是多少？

(1)、方法探究

对于立体图形中求最短路程问题，应把立体图形展开成平面图形，再确定A ， B两点的位置，依据“两点之间线段最短”，结合勾股定理，解决相应的问题．如图2，在圆柱的侧面展开图中，点A ， B对应的位置如图所示，利用勾股定理求出蚂蚁爬行的最短路程是cm．

(2)、方法应用

如图3，直四棱柱的上下底面是正方形，底面边长为3cm，高为10cm．在其侧面从点A开始，绕侧面两周，嵌入装饰彩条至点B停止．求彩条的最短长度．

(3)、如图4，圆柱形玻璃杯底面周长为30cm，高为35 cm，杯底厚1cm．在玻璃杯外壁距杯口2cm的点A处有一只蚂蚁，蚂蚁相对面的内壁底部B处有一滴蜂蜜，蚂蚁沿杯口爬入内壁去吃蜂蜜，求蚂蚁爬行的最短路径长．（玻璃杯的壁厚忽略不计）

查看试题解析

三、拓展创新

21. 有一个面积为1的正方形，经过一次“生长”后，在他的左右肩上生出两个小正方形，其中，三个正方形围成的三角形是直角三角形，再经过一次“生长”后，变成了下图，如果继续“生长”下去，它将变得“枝繁叶茂”，请你算出“生长”了2019次后形成的图形中所有的正方形的面积和是（）

A、1 B、2018 C、2019 D、2020

查看试题解析

22. 嘉嘉参加机器人设计活动，需操控机器人在5×5的方格棋盘上从A点行走至B点，且每个小方格皆为正方形，主办单位规定了三条行走路径R₁ ， R₂ ， R₃ ，其行经位置如图与表所示：

路径	编号	图例	行径位置
第一条路径	R₁		A→C→D→B
第二条路径	R₂		A→E→D→F→B
第三条路径	R₃		A→G→B

已知A、B、C、D、E、F、G七点皆落在格线的交点上，且两点之间的路径皆为直线，在无法使用任何工具测量的条件下，请判断R₁、R₂、R₃这三条路径中，最长与最短的路径分别为何？请写出你的答案，并完整说明理由．

查看试题解析