浙教版数学八年级上册期中模拟测试卷 B
试卷更新日期:2024-10-26 类型:期中考试
一、选择题(每题3分,共30分)
-
1. 下列交通标志中,属于轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 将三角尺按如图位置摆放,顶点A落在直线上,顶点B落在直线上,若 , , 则的度数是( )
2. 将三角尺按如图位置摆放,顶点A落在直线上,顶点B落在直线上,若 , , 则的度数是( ) A、 B、 C、 D、3. 不等式组的解集在数轴上表示为( )A、
A、 B、 C、 D、3. 不等式组的解集在数轴上表示为( )A、 B、
B、 C、
C、 D、
D、 4. 如图为商场某品牌椅子的侧面图, , 与地面平行, , 则( )
4. 如图为商场某品牌椅子的侧面图, , 与地面平行, , 则( ) A、70° B、65° C、60° D、50°5. 某单位为响应政府号召,需要购买分类垃圾桶6个,市场上有A型和B型两种分类垃圾桶,A型分类垃圾桶500元/个,B型分类垃圾桶550元/个,总费用不超过3100元,则不同的购买方式有( )A、2种 B、3种 C、4种 D、5种6. 小明用两个全等的等腰三角形设计了一个“蝴蝶”的平面图案,如图.其中与都是等腰三角形,且它们关于直线对称,点分别是底边的中点, . 下列推断错误的是( )
A、70° B、65° C、60° D、50°5. 某单位为响应政府号召,需要购买分类垃圾桶6个,市场上有A型和B型两种分类垃圾桶,A型分类垃圾桶500元/个,B型分类垃圾桶550元/个,总费用不超过3100元,则不同的购买方式有( )A、2种 B、3种 C、4种 D、5种6. 小明用两个全等的等腰三角形设计了一个“蝴蝶”的平面图案,如图.其中与都是等腰三角形,且它们关于直线对称,点分别是底边的中点, . 下列推断错误的是( ) A、 B、 C、 D、7. “今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问:水深几何?”这是我国数学史上的“葭生池中”问题.即AC=5,DC=1,BD=BA , 则BC=( )
A、 B、 C、 D、7. “今有方池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐.问:水深几何?”这是我国数学史上的“葭生池中”问题.即AC=5,DC=1,BD=BA , 则BC=( ) A、8 B、10 C、12 D、138. 如图,在中, , , 为边的中点,点 , 分别在边 , 上, , 则四边形的面积为( )
A、8 B、10 C、12 D、138. 如图,在中, , , 为边的中点,点 , 分别在边 , 上, , 则四边形的面积为( ) A、18 B、 C、9 D、9. “赵爽弦图”巧妙利用面积关系证明了勾股定理.如图所示的“赵爽弦图”是由四个全等直角三角形和中间的小正方形拼成的一个大正方形.设直角三角形的两条直角边长分别为m , n(m>n).若小正方形面积为5,(m+n)2=21,则大正方形面积为( )
A、18 B、 C、9 D、9. “赵爽弦图”巧妙利用面积关系证明了勾股定理.如图所示的“赵爽弦图”是由四个全等直角三角形和中间的小正方形拼成的一个大正方形.设直角三角形的两条直角边长分别为m , n(m>n).若小正方形面积为5,(m+n)2=21,则大正方形面积为( ) A、12 B、13 C、14 D、1510. 如图1,与满足 , , , , 我们称这样的两个三角形为“伪全等三角形”
A、12 B、13 C、14 D、1510. 如图1,与满足 , , , , 我们称这样的两个三角形为“伪全等三角形”
如图2,在中, , 点D , E在线段上,且 , 则图中共有“伪全等三角形”( )
A、1对 B、2对 C、3对 D、4对二、填空题(每题3分,共18分)
-
11. 命题“若a>b , 则a﹣3<b﹣3”是命题.(填“真”或“假”)12. 如图,已知l1∥l2 , △ABC是等腰直角三角形,∠BAC=90°,顶点A , B分别在l1 , l2上,当∠1=70°时,∠2=°.
 13. 关于x的不等式组恰有3个整数解,则a的取值范围是 .14. 如图, , 与交于点O,请添加一个条件 , 使 . (只填一种情况即可)
13. 关于x的不等式组恰有3个整数解,则a的取值范围是 .14. 如图, , 与交于点O,请添加一个条件 , 使 . (只填一种情况即可)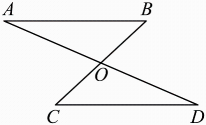 15. 如图, 已知 , 点 为 内部一点, 点 为射线 、点 为射线 上的两个动点, 当 的周长最小时, 则 。
15. 如图, 已知 , 点 为 内部一点, 点 为射线 、点 为射线 上的两个动点, 当 的周长最小时, 则 。 16. 如图①,直角三角形的两个锐角分别是40°和50°,其三边上分别有一个正方形.执行下面的操作:由两个小正方形向外分别作锐角为40°和50°的直角三角形,再分别以所得到的直角三角形的直角边为边长作正方形.图②是1次操作后的图形.图③是重复上述步骤若干次后得到的图形,人们把它称为“毕达哥拉斯树”.若图①中的直角三角形斜边长为2,则10次操作后图形中所有正方形的面积和为 .
16. 如图①,直角三角形的两个锐角分别是40°和50°,其三边上分别有一个正方形.执行下面的操作:由两个小正方形向外分别作锐角为40°和50°的直角三角形,再分别以所得到的直角三角形的直角边为边长作正方形.图②是1次操作后的图形.图③是重复上述步骤若干次后得到的图形,人们把它称为“毕达哥拉斯树”.若图①中的直角三角形斜边长为2,则10次操作后图形中所有正方形的面积和为 .
三、解答题(共9题,共72分)
-
17. 解不等式: , 把它的解集表示在数轴上.
 18. 解不等式组: , 并写出它的所有整数解.19. 如图,B、E、C、F是直线l上的四点,AC、DE相交于点G , AB=DF , AC=DE , BC=EF .
18. 解不等式组: , 并写出它的所有整数解.19. 如图,B、E、C、F是直线l上的四点,AC、DE相交于点G , AB=DF , AC=DE , BC=EF . (1)、求证:△GEC是等腰三角形;(2)、连接AD , 则AD与l的位置关系是 .20. 在数学活动课上,王老师要求学生将图1所示的3×3正方形方格纸,剪掉其中两个方格,使之成为轴对称图形.规定:凡通过旋转能重合的图形视为同一种图形,如图2的四幅图就视为同一种设计方案(阴影部分为要剪掉部分)
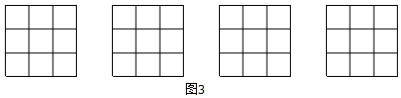
(1)、求证:△GEC是等腰三角形;(2)、连接AD , 则AD与l的位置关系是 .20. 在数学活动课上,王老师要求学生将图1所示的3×3正方形方格纸,剪掉其中两个方格,使之成为轴对称图形.规定:凡通过旋转能重合的图形视为同一种图形,如图2的四幅图就视为同一种设计方案(阴影部分为要剪掉部分)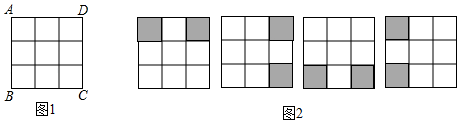
请在图中画出4种不同的设计方案,将每种方案中要剪掉的两个方格涂黑(每个3×3的正方形方格画一种,例图除外)
 21. 为提升学生身体素质,落实教育部门“在校学生每天锻炼时间不少于1小时”的文件精神.某校利用课后服务时间,在八年级开展“体育赋能,助力成长”班级篮球赛,共个班级参加.(1)、比赛积分规定:每场比赛都要分出胜负,胜一场积分,负一场积分.某班级在场比赛中获得总积分为分,问该班级胜负场数分别是多少?(2)、投篮得分规则:在分线外投篮,投中一球可得分,在分线内含分线投篮,投中一球可得分,某班级在其中一场比赛中,共投中个球只有分球和分球 , 所得总分不少于分,问该班级这场比赛中至少投中了多少个分球?22. 如图,在和中, , , , 且点D在线段上,连 .
21. 为提升学生身体素质,落实教育部门“在校学生每天锻炼时间不少于1小时”的文件精神.某校利用课后服务时间,在八年级开展“体育赋能,助力成长”班级篮球赛,共个班级参加.(1)、比赛积分规定:每场比赛都要分出胜负,胜一场积分,负一场积分.某班级在场比赛中获得总积分为分,问该班级胜负场数分别是多少?(2)、投篮得分规则:在分线外投篮,投中一球可得分,在分线内含分线投篮,投中一球可得分,某班级在其中一场比赛中,共投中个球只有分球和分球 , 所得总分不少于分,问该班级这场比赛中至少投中了多少个分球?22. 如图,在和中, , , , 且点D在线段上,连 .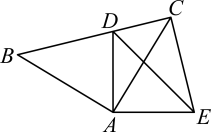 (1)、求证:;(2)、若 , 求的度数.23.(1)、【探究】
(1)、求证:;(2)、若 , 求的度数.23.(1)、【探究】已知和都是等边三角形.

①如图1,当点在BC上时,连接CE.请探究CA,CE和CD之间的数是关系,并说明理由;
②如图2,当点D在线段BC的延长线上时,连接CE.请再次探究CA,CE和CD之间的数量关系,并说明理由.
(2)、【运用】如图3,等边三角形ABC中, , 点在AC上,.点是直线BC上的动点,连接DE,以DE为边在DE的右侧作等边三角形DEF,连接CF.当为直角三角形时,请直接写出BD的长.
24. 【阅读理解】已知 , , 是三个实数,表示 , , 这三个数的平均数,表示 , , 这三个数中最小的数.
如 , ;
, ;
解决下列问题:
(1)、若 , 求的取值范围;(2)、若 , 求的值:(3)、由(2)可得结论:“若 , 则______”(填 , , 的大小关系),运用这个结论解决问题:若 , 求的值.25. 阅读下列材料,并回答问题.画一个直角三角形,使它的两条直角边分别为5和12,那么我们可以量得直角三角形的斜边长为13,并且事实上,在任何一个直角三角形中,两条直角边的平方之和一定等于斜边的平方.如果直角三角形中,两直角边长分别为a、b,斜边长为c,则这个结论就是著名的勾股定理.
请利用这个结论,完成下面的活动:
(1)、一个直角三角形的两条直角边分别为6、8,那么这个直角三角形斜边长为 .(2)、满足勾股定理方程的正整数组叫勾股数组.例如就是一组勾股数组.观察下列几组勾股数①3,4,5; ②5,12,13; ③7,24,25;④9,40,41;
请你写出有以上规律的第⑤组勾股数: .
(3)、如图,于D, , 求的长度.