甘肃省兰州三十六中2017年中考数学模拟试卷（五）

试卷更新日期：2017-12-07 类型：中考模拟

进入出卷网下载

一、选择题：

1. 下列说法中，正确的是（）

A、两条对角线相等的四边形是平行四边形 B、两条对角线相等且互相垂直的四边形是矩形 C、两条对角线互相垂直平分的四边形是菱形 D、两条对角线互相垂直平分且相等的四边形是菱形

查看试题解析
2. 下列函数中，是二次函数的有（）
①y=1﹣ $\sqrt{2}$ x²②y= $\frac{1}{x^{2}}$ ③y=x（1﹣x）④y=（1﹣2x）（1+2x）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 若二次函数y=x²﹣6x+9的图象经过A（﹣1，y₁），B（1，y₂），C（3+ $\sqrt{3}$ ，y₃）三点．则关于y₁ ， y₂ ， y₃大小关系正确的是（）

A、y₁＞y₂＞y₃ B、y₁＞y₃＞y₂ C、y₂＞y₁＞y₃ D、y₃＞y₁＞y₂

查看试题解析
4. 菱形的周长为8cm，高为1cm，则菱形两邻角度数比为（）

A、4：1 B、5：1 C、6：1 D、7：1

查看试题解析
5.
如图，在△ABC中，DE∥BC，AD=6，DB=3，AE=4，则EC的长为（）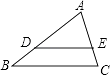

A、1 B、2 C、3 D、4

查看试题解析
6. 如图，已知⊙O是△ABD的外接圆，AB是⊙O的直径，CD是⊙O的弦，∠ABD=58°，则∠BCD等于（）

A、116° B、32° C、58° D、64°

查看试题解析
7. 在某次聚会上，每两人都握了一次手，所有人共握手10次，设有x人参加这次聚会，则列出方程正确的是（）

A、x（x﹣1）=10 B、 $\frac{x (x - 1)}{2}$ =10 C、x（x+1）=10 D、 $\frac{x (x + 1)}{2}$ =10

查看试题解析
8. 如图，直线l和双曲线 $y = \frac{k}{x} (k > 0)$ 交于A、B两点，P是线段AB上的点（不与A，B重合），过点A，B，P分别向x轴作垂线，垂足分别为C，D，E，连接OA，OB，0P，设△AOC的面积为S₁、△BOD的面积为S₂、△POE的面积为S₃ ，则（）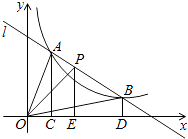

A、S₁＜S₂＜S₃ B、S₁＞S₂＞S₃ C、S₁=S₂＞S₃ D、S₁=S₂＜S₃

查看试题解析
9. 如图，在平行四边形ABCD中，AB=9，AD=6，∠ADC的平分线交AB于点E，交CB的延长线于点F，AG⊥DE，垂足为G．若AG=4 $\sqrt{2}$ ，则△BEF的面积是（）

A、 $\sqrt{2}$ B、2 $\sqrt{2}$ C、3 $\sqrt{2}$ D、4 $\sqrt{2}$

查看试题解析
10. 圆的半径扩大一倍，则它的相应的圆内接正n边形的边长与半径之比（）

A、扩大了一倍 B、扩大了两倍 C、扩大了四倍 D、没有变化

查看试题解析
11. 心理学家发现：学生对概念的接受能力y与提出概念的时间x（min）之间是二次函数关系，当提出概念13min时，学生对概念的接受力最大，为59.9；当提出概念30min时，学生对概念的接受能力就剩下31，则y与x满足的二次函数关系式为（）

A、y=﹣（x﹣13）²+59.9 B、y=﹣0.1x²+2.6x+31 C、y=0.1x²﹣2.6x+76.8 D、y=﹣0.1x²+2.6x+43

查看试题解析
12. 如图，抛物线y=ax²+bx+c的对称轴是x=﹣1．且过点（0.5，0），有下列结论：
①abc＞0； ②a﹣2b+4c=0； ③25a﹣10b+4c=0； ④3b+2c＞0；⑤a﹣b≥m（am﹣b）．
其中所有正确的结论是（）

A、①②③ B、①③④ C、①②③⑤ D、①③⑤

查看试题解析

二、填空题：

13. 已知x²+3x+5的值为11，则代数式3x²+9x+12的值为．

查看试题解析
14. 如图，在菱形ABCD中，AC、BD相交于点O，E为AB的中点，若OE=2，则菱形ABCD的周长是．

查看试题解析
15. 如图，已知⊙O的半径为2，A为⊙O外一点，过点A作⊙O的一条切线AB，切点是B，AO的延长线交⊙O于点C，若∠BAC=30°，则劣弧 $\hat{B C}$ 的长为．

查看试题解析
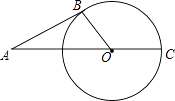16. 在平面直角坐标系中，正方形ABCD的位置如右图所示，点A的坐标为（1，0），点D的坐标为（0，2）．延长CB交x轴于点A₁ ，作正方形A₁B₁C₁C；延长C₁B₁交x轴于点A₂ ，作正方形A₂B₂C₂C₁ ， …按这样的规律进行下去，第2017个正方形的面积为．

查看试题解析
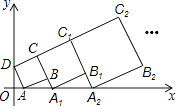17. 如图，正方形ABCD的边长为4，点E在BC上，四边形EFGB也是正方形，以B为圆心，BA长为半径画 $\hat{A C}$ ，连结AF，CF，则图中阴影部分面积为．

查看试题解析

三、计算题：

18. 计算：3tan30°﹣2tan45°+2sin60°+4cos60°．

查看试题解析
19. 解方程：（x﹣1）（x﹣3）=8．

查看试题解析

四、解答题：

20. 如图，将△ABC在网格中（网格中每个小正方形的边长均为1）依次进行位似变换、轴对称变换和平移变换后得到△A₃B₃C₃ ．

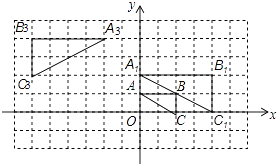(1)、△ABC与△A₁B₁C₁的位似比等于；

(2)、在网格中画出△A₁B₁C₁关于y轴的轴对称图形△A₂B₂C₂；

(3)、请写出△A₃B₃C₃是由△A₂B₂C₂怎样平移得到的？

(4)、设点P（x，y）为△ABC内一点，依次经过上述三次变换后，点P的对应点的坐标为．

查看试题解析
21. 2016年3月全国两会胜利召开，某数学兴趣小组就两会期间出现频率最高的热词：A脱贫攻坚．B．绿色发展．C．自主创新．D．简政放权等热词进行了抽样调查，每个同学只能从中选择一个“我最关注”的热词，如图是根据调查结果绘制的两幅不完整的统计图．
请你根据统计图提供的信息，解答下列问题：

(1)、本次调查中，一共调查了名同学；

(2)、条形统计图中，m= ， n=；

(3)、扇形统计图中，热词B所在扇形的圆心角的度数是；

(4)、从该校学生中随机抽取一个最关注热词D的学生的概率是多少？

查看试题解析
22. 张老师利用休息时间组织学生测量山坡上一棵大树CD的高度，如图，山坡与水平面成30°角（即∠MAN=30°），在山坡底部A处测得大树顶端点C的仰角为45°，沿坡面前进20米，到达B处，又测得树顶端点C的仰角为60°（图中各点均在同一平面内），求这棵大树CD的高度（结果精确到0.1米，参考数据： $\sqrt{3}$ ≈1.732）

查看试题解析
23. 如图，在△ABC中，AC=BC，D是BC上的一点，且满足∠BAD= $\frac{1}{2}$ ∠C，以AD为直径的⊙O与AB，AC分别相交于点E，F．

(1)、求证：直线BC是⊙O的切线；

(2)、连接EF，若tan∠AEF= $\frac{4}{3}$ ，AD=4，求BD的长．

查看试题解析
24. 在正方形ABCD中，对角线AC，BD交于点O，点P在线段BC上（不含点B），∠BPE= $\frac{1}{2}$ ∠ACB，PE交BO于点E，过点B作BF⊥PE，垂足为F，交AC于点G．

(1)、当点P与点C重合时（如图①），求证：△BOG≌△POE；

(2)、结合图②，通过观察、测量、猜想： $\frac{B F}{P E}$ 与 $\frac{1}{2}$ 的关系，并证明你的猜想；

(3)、把正方形ABCD改为菱形，其他条件不变（如图③），若AC=8，BD=6，直接写出 $\frac{B F}{P E}$ 的值．

查看试题解析