浙教版数学八年级上册期中模拟测试卷 A
试卷更新日期:2024-10-26 类型:期中考试
一、选择题(每题3分,共30分)
-
1. 现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性。下列汉字是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 小明将一块直角三角板摆放在直尺上,如图,若∠1=55°,则∠2的度数为( )
2. 小明将一块直角三角板摆放在直尺上,如图,若∠1=55°,则∠2的度数为( ) A、25° B、35° C、45° D、55°3. 如果 , 那么下列正确的是( )A、 B、 C、 D、4. 如图,直线m∥n , 一块含有30°的直角三角板按如图所示放置.若∠1=40°,则∠2的大小为( )
A、25° B、35° C、45° D、55°3. 如果 , 那么下列正确的是( )A、 B、 C、 D、4. 如图,直线m∥n , 一块含有30°的直角三角板按如图所示放置.若∠1=40°,则∠2的大小为( ) A、70° B、60° C、50° D、40°5. 如图,已知△ABC≌△DEC , ∠A=60°,∠B=40°,则∠DCE的度数为 ( )
A、70° B、60° C、50° D、40°5. 如图,已知△ABC≌△DEC , ∠A=60°,∠B=40°,则∠DCE的度数为 ( ) A、40° B、60° C、80° D、100°6. 不等式组的解集在数轴上表示为( )A、
A、40° B、60° C、80° D、100°6. 不等式组的解集在数轴上表示为( )A、 B、
B、 C、
C、 D、
D、 7. 如图,直线l∥m,等边三角形ABC的两个顶点B,C分别落在直线l,m上,若∠ABE=21°,则∠ACD的度数是( )
7. 如图,直线l∥m,等边三角形ABC的两个顶点B,C分别落在直线l,m上,若∠ABE=21°,则∠ACD的度数是( ) A、 B、 C、 D、8. 如图,AB∥CD,点E在线段BC上,CD=CE.若∠ABC=30°,则∠D为( )
A、 B、 C、 D、8. 如图,AB∥CD,点E在线段BC上,CD=CE.若∠ABC=30°,则∠D为( ) A、85° B、75° C、60° D、30°9. 如图1是第七届国际数学教育大会()的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能够组合得到如图2所示的四边形.若 , , , 则的值为( )
A、85° B、75° C、60° D、30°9. 如图1是第七届国际数学教育大会()的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能够组合得到如图2所示的四边形.若 , , , 则的值为( )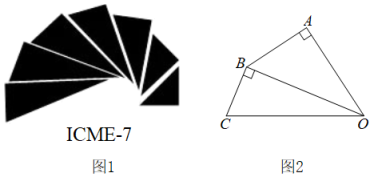 A、 B、 C、 D、1
A、 B、 C、 D、1二、填空题(每题3分,共18分)
-
10. 请写出命题“如果 ,那么 ”的逆命题:.11. 一个三角形的三边长之比是5:12:13,且周长是60,则它的面积是 .12. 如图, , 若 , , 则的度数为.
 13. 等腰三角形的两边长分别为 ,其周长为cm.14. 如图,直线MN∥PQ,直线AB分别与MN,PQ相交于点A,B.小宇同学利用尺规按以下步骤作图:①以点A为圆心,以任意长为半径作弧交AN于点C,交AB于点D;②分别以C,D为圆心,以大于 CD长为半径作弧,两弧在∠NAB内交于点E;③作射线AE交PQ于点F.若AB=2,∠ABP=60°,则线段AF的长为 .
13. 等腰三角形的两边长分别为 ,其周长为cm.14. 如图,直线MN∥PQ,直线AB分别与MN,PQ相交于点A,B.小宇同学利用尺规按以下步骤作图:①以点A为圆心,以任意长为半径作弧交AN于点C,交AB于点D;②分别以C,D为圆心,以大于 CD长为半径作弧,两弧在∠NAB内交于点E;③作射线AE交PQ于点F.若AB=2,∠ABP=60°,则线段AF的长为 .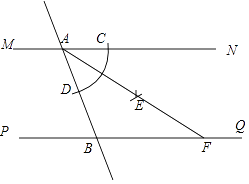 15. 关于x的一元一次不等式组恰有一个整数解,则m的取值范围是 .
15. 关于x的一元一次不等式组恰有一个整数解,则m的取值范围是 .三、解答题(共9题,共72分)
-
16. 解不等式组:17. 解不等式组 ,并把解集在数轴上表示出来.18. 如图,∠C=∠D=90°,∠CBA=∠DAB .
 (1)、求证:△ABC≌△BAD;(2)、若∠DAB=70°,则∠CAB=°.19. 某中学组织学生研学,原计划租用可坐乘客人的种客车若干辆,则有人没有座位;若租用可坐乘客人的种客车,则可少租辆,且恰好坐满.(1)、求原计划租用种客车多少辆?这次研学去了多少人?(2)、若该校计划租用、两种客车共辆,要求种客车不超过辆,且每人都有座位,则有哪几种租车方案?(3)、在(2)的条件下,若种客车租金为每辆元,种客车租金每辆元,应该怎样租车才最合算?20. 如图,在四边形中,点E是边上一点,且 , .
(1)、求证:△ABC≌△BAD;(2)、若∠DAB=70°,则∠CAB=°.19. 某中学组织学生研学,原计划租用可坐乘客人的种客车若干辆,则有人没有座位;若租用可坐乘客人的种客车,则可少租辆,且恰好坐满.(1)、求原计划租用种客车多少辆?这次研学去了多少人?(2)、若该校计划租用、两种客车共辆,要求种客车不超过辆,且每人都有座位,则有哪几种租车方案?(3)、在(2)的条件下,若种客车租金为每辆元,种客车租金每辆元,应该怎样租车才最合算?20. 如图,在四边形中,点E是边上一点,且 , . (1)、求证:;(2)、若 , 时,求的面积.21. 国旗是一个国家的象征和标志,每周一次的校园升旗仪式让我们感受到祖国的伟大,心中充满了自豪和敬仰某校“综合与实践”小组开展了测量本校旗杆高度的实践活动他们制订了测量方案,并利用课余时间完成了实地测量,测量结果如下表不完整 .
(1)、求证:;(2)、若 , 时,求的面积.21. 国旗是一个国家的象征和标志,每周一次的校园升旗仪式让我们感受到祖国的伟大,心中充满了自豪和敬仰某校“综合与实践”小组开展了测量本校旗杆高度的实践活动他们制订了测量方案,并利用课余时间完成了实地测量,测量结果如下表不完整 .课题
测量学校旗杆的高度
成员
组长:组员: , ,
工具
皮尺等
测量示意图

说明:线段表示学校旗杆,垂直地面于点 , 如图 , 第一次将系在旗杆顶端的绳子垂直到地面,并多出了一段 , 用皮尺测出的长度;如图 , 第二次将绳子拉直,绳子末端落在地面的点处,用皮尺测出的距离.
测量数据
测量项目
数值
图中的长度
米
图中的长度
米
(1)、根据以上测量结果,请你帮助该“综合与实践”小组求出学校旗杆的高度;(2)、该校礼仪队要求旗手在不少于秒且不超过秒的时间内将五星红旗从旗杆底部处升至顶部处,已知五星红旗沿着旗杆滑动的这一边长度为厘米,求五星红旗升起的平均速度取值范围计算结果精确到 .22. 综合与实践课上,李老师以“发现-探究-拓展”的形式,培养学生数学思想,训练学生数学思维.以下是李老师的课堂主题展示: (1)、如图,在等腰△ABC中,AC=BC , 点D为线段AB上的一动点(点D不与A , B重合),以CD为边作等腰△CDE , CD=CE , ∠ACB=∠DCE= , 连接BE.解答下列问题:
(1)、如图,在等腰△ABC中,AC=BC , 点D为线段AB上的一动点(点D不与A , B重合),以CD为边作等腰△CDE , CD=CE , ∠ACB=∠DCE= , 连接BE.解答下列问题:①【观察发现】
如图1,当时,线段AD , BE的数量关系为 ▲ , .∠ABE= ▲ °;
②【类比探究】
如图2,当时,试探究线段AC与BE的位置关系,并说明理由;
(2)、【拓展延伸】如图3,四边形ABCD中,∠BAD=∠BCD=90°,AB=AD , 连接AC , 若AC=8,则四边形ABCD的面积为多少?(直接写出结果).
23. 综合与运用阅读理解:若一元一次方程的解在一元一次不等式组解集范围内,则称该一元一次方程为该不等式组的“友好方程”,例如:方程的解为 , 而不等式组的解集为 , 不难发现在的范围内,所以方程是不等式组的“友好方程”.
(1)、在方程①;②;③中,不等式组的“友好方程”是;(填序号)(2)、若关于x的方程是不等式组的“友好方程”,求k的取值范围.24. 如图1,把一块直角三角尺的直角顶点C放置在水平直线上,在中, , , 试回答下列问题: (1)、若把三角尺绕着点C按顺时针方向旋转,当时,度;(2)、在三角尺绕着点C按顺时针方向旋转过程中,分别作于M , 与N , 若 , , 求.(3)、三角尺绕着点C按顺时针方向继续旋转到图3的位置,其他条件不变,则、与之间有什么关系?请说明理由.
(1)、若把三角尺绕着点C按顺时针方向旋转,当时,度;(2)、在三角尺绕着点C按顺时针方向旋转过程中,分别作于M , 与N , 若 , , 求.(3)、三角尺绕着点C按顺时针方向继续旋转到图3的位置,其他条件不变,则、与之间有什么关系?请说明理由.