福建省漳州市2017年中考数学模拟试卷（5月份）

试卷更新日期：2017-12-07 类型：中考模拟

进入出卷网下载

一、选择题

1. 如图，点A，B，C，D在数轴上，其中表示互为相反数的点是（）

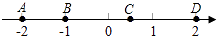A、点A与点D B、点B与点D C、点A与点C D、点B与点C

查看试题解析
2. 如图，一个水平放置的六棱柱，这个六棱柱的左视图是（）

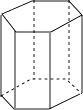A、 B、 C、 D、

查看试题解析
3. a⁶可以表示为（）

A、a³•a² B、（a²）³ C、a¹²÷a² D、a⁷﹣a

查看试题解析
4. 下列交通标志中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
5. 若﹣ $\frac{1}{2}$ a≥b，则a≤﹣2b，其根据是（）

A、不等式的两边都加上（或减去）同一个整式，不等号的方向不变 B、不等式的两边都乘（或除以）同一个正数，不等号的方向不变 C、不等式的两边都乘（或除以）同一个负数，不等号的方向改变 D、以上答案均不对

查看试题解析
6. 若一组数据3，x，4，5，6的众数是5，则这组数据的中位数是（）

A、3 B、4 C、5 D、6

查看试题解析
7. 2016年漳州市生产总值突破3000亿元，数字3000亿用科学记数法表示为（）

A、3×10¹² B、30×10¹¹ C、0.3×10¹¹ D、3×10¹¹

查看试题解析
8. 如图，在△ABC中，AB=5，BC=3，AC=4，点E，F分别是AB，BC的中点．以下结论错误的是（）

A、△ABC是直角三角形 B、AF是△ABC的中位线 C、EF是△ABC的中位线 D、△BEF的周长为6

查看试题解析
9. 如图，点 O是△ABC外接圆的圆心，若⊙O的半径为5，∠A=45°，则 $\hat{B C}$ 的长是（）

A、 $\frac{5}{8}$ π B、 $\frac{25}{4}$ π C、 $\frac{5}{4}$ π D、 $\frac{5}{2}$ π

查看试题解析
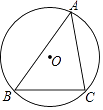10. 如图1，在矩形ABCD中，动点P从点B出发，沿BC→CD→DA运动至点A停止．设点P运动的路程为x，△ABP的面积为y，y关于x的函数图象如图2所示，则m的值是（）

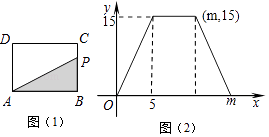A、6 B、8 C、11 D、16

查看试题解析

二、填空题

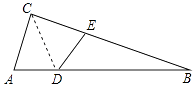
11. 分解因式：x³﹣4x²y+4xy²= ．

查看试题解析
12. 已知正n边形的一个内角为135°，则边数n的值是．

查看试题解析
13. 在一个不透明的布袋中装有4个红球和a个白球，它们除颜色不同外，其余均相同，若从中随机摸出一球，摸到红球的概率是 $\frac{2}{5}$ ，则a的值是．

查看试题解析
14. 如图，在△ABC中，∠ACB=90°，将△ACD沿CD折叠，使点A恰好落在BC边上的点E处．若∠B=25°，则∠BDE=度．

查看试题解析
15. 若实数a满足a²﹣2a﹣1=0，则2a²﹣4a+2015的值是．

查看试题解析
16. 定义：式子1﹣ $\frac{1}{a}$ （a≠0）叫做a的影子数．如：3的影子数是1﹣ $\frac{1}{3}$ = $\frac{2}{3}$ ，已知a₁=﹣ $\frac{1}{2}$ ，a₂是a₁的影子数，a₃是a₂的影子数，…，依此类推，则a₂₀₁₇的值是．

查看试题解析

三、解答题

17. 计算：| $\sqrt{3}$ ﹣2|+3tan30°+2^﹣² ．

查看试题解析
18. 先化简，再求值： $(1 - \frac{x}{x + 1}) \div \frac{x}{x + 1}$ ，其中x=2．

查看试题解析
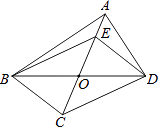
19. 如图，在8×8的正方形网格中，△ABC的顶点和线段EF的端点都在边长为1的小正方形的格点上．请你在图中找出一点D（仅一个点即可），连结DE，DF，使△DEF与△ABC全等，并给予证明．

查看试题解析
20. 如图，在四边形ABCD中，对角线AC，BD相交于点O，且OB=OD．点E在线段OA上，连结BE，DE．给出下列条件：①OC=OE；②AB=AD；③BC⊥CD；④∠CBD=∠EBD．请你从中选择两个条件，使四边形BCDE是菱形，并给予证明．你选择的条件是：（只填写序号）．

查看试题解析
21. 为了落实漳州市教育局关于全市中小学生每天阅读1小时的文件精神．某校对七年级（3）班全体学生一周到图书馆的次数做了调查统计，以下是调查过程中绘制的还不完整的两个统计图．请你根据统计图表中的信息，解答下列问题：
七年级（3）班学生到图书馆的次数统计表
到图书馆的
次数
0次
1次
2次
3次
4次及
以上
人数
5
10
m
8
12

(1)、求图表中m，n的值；

(2)、该年级学生共有300人，估计这周到图书馆的次数为“4次及以上”的学生大约有多少人？

查看试题解析
22. 如图，直线y₁=kx+2与反比例函数y₂= $\frac{3}{x}$ 的图象交于点A（m，3），与坐标轴分别交于B，C两点．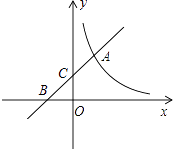

(1)、若y₁＞y₂＞0，求自变量x的取值范围；

(2)、动点P（n，0）在x轴上运动，当n为何值时，|PA﹣PC|的值最大？并求最大值．

查看试题解析
23. 如图，在△ABC中，AC=BC，以BC边为直径作⊙O交AB边于点D，过点D作DE⊥AC于点E．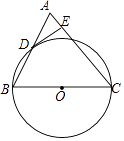

(1)、求证：DE是⊙O的切线；

(2)、若⊙O的半径等于 $\frac{3}{2}$ ，cosB= $\frac{1}{3}$ ，求线段DE的长．

查看试题解析
24. 如图，已知抛物线y=x²+bx+c与直线y=﹣x+3相交于坐标轴上的A，B两点，顶点为C．

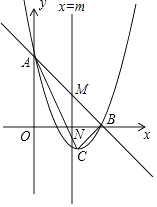(1)、填空：b= ， c=；

(2)、将直线AB向下平移h个单位长度，得直线EF．当h为何值时，直线EF与抛物线y=x²+bx+c没有交点？

(3)、直线x=m与△ABC的边AB，AC分别交于点M，N．当直线x=m把△ABC的面积分为1：2两部分时，求m的值．

查看试题解析
25. 操作与探究
综合实践课，老师把一个足够大的等腰直角三角尺AMN靠在一个正方形纸片ABCD的一侧，使边AM与AD在同
一直线上（如图1），其中∠AMN=90°，AM=MN．

(1)、猜想发现
老师将三角尺AMN绕点A逆时针旋转α．如图2，当0＜α＜45°时，边AM，AN分别与直线BC，CD交于点E，F，连结EF．小明同学探究发现，线段EF，BE，DF满足EF=BE﹣DF；如图3，当45°＜α＜90°时，其它条件不变．
①填空：∠DAF+∠BAE=度；
②猜想：线段EF，BE，DF三者之间的数量关系是：．

(2)、证明你的猜想；

(3)、拓展探究
在45°＜α＜90°的情形下，连结BD，分别交AM，AN于点G，H，如图4连结EH，试证明：EH⊥AN．

查看试题解析