福建省福州教育学院二附中2017年中考数学二模试卷
试卷更新日期:2017-12-07 类型:中考模拟
一、选择题
-
1. 中国古代数学著作《九章算术》的“方程”一章,在世界数学史上首次正式引入负数,如果收入120元记作+120元,那么﹣100元表示( )A、支出20元 B、收入20元 C、支出100元 D、收入100元2. 下列几何体中,有一个几何体的主视图与俯视图的形状不一样,这个几何体是( )A、
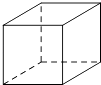 正方体
B、
正方体
B、 圆柱
C、
圆柱
C、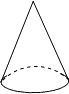 圆椎
D、
圆椎
D、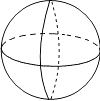 球
3. 截至5月21日,全县完成工业开票销售337.53亿元,337.53亿元用科学记数法表示为( )元.A、33.753×109 B、3.3753×1010 C、0.33753×1011 D、0.033753×10124. 下面的四幅简笔画是从文化活动中抽象出来的,其中是轴对称图形的是( )A、
球
3. 截至5月21日,全县完成工业开票销售337.53亿元,337.53亿元用科学记数法表示为( )元.A、33.753×109 B、3.3753×1010 C、0.33753×1011 D、0.033753×10124. 下面的四幅简笔画是从文化活动中抽象出来的,其中是轴对称图形的是( )A、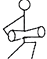 B、
B、 C、
C、 D、
D、 5. 如图所示,直线AB,CD相交于点O,且∠AOD+∠BOC=100°,则∠AOC是( )
5. 如图所示,直线AB,CD相交于点O,且∠AOD+∠BOC=100°,则∠AOC是( ) A、150° B、130° C、100° D、90°6. 一个不透明的口袋中有6个白球和12个黑球,“任意摸出n个球,其中至少有一个白球”是必然事件,n等于( )A、6 B、7 C、13 D、187. 如图,在⊙O中, = ,∠AOB=40°,则∠ADC的度数是( )
A、150° B、130° C、100° D、90°6. 一个不透明的口袋中有6个白球和12个黑球,“任意摸出n个球,其中至少有一个白球”是必然事件,n等于( )A、6 B、7 C、13 D、187. 如图,在⊙O中, = ,∠AOB=40°,则∠ADC的度数是( )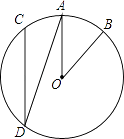 A、40° B、30° C、20° D、15°8. 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于 MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )
A、40° B、30° C、20° D、15°8. 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M、N为圆心,大于 MN的长为半径画弧,两弧在第二象限交于点P.若点P的坐标为(2a,b+1),则a与b的数量关系为( )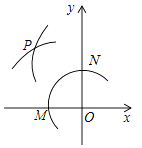 A、a=b B、2a﹣b=1 C、2a+b=﹣1 D、2a+b=19. 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,3 ),反比例函数y= 的图象与菱形对角线AO交D点,连接BD,当DB⊥x轴时,k的值是( )
A、a=b B、2a﹣b=1 C、2a+b=﹣1 D、2a+b=19. 如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,3 ),反比例函数y= 的图象与菱形对角线AO交D点,连接BD,当DB⊥x轴时,k的值是( ) A、6 B、﹣6 C、12 D、﹣1210. 如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,点M为边AB上的一动点,点N为边AC上的一动点,且∠MDN=90°,则cos∠DMN为( )
A、6 B、﹣6 C、12 D、﹣1210. 如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,点M为边AB上的一动点,点N为边AC上的一动点,且∠MDN=90°,则cos∠DMN为( )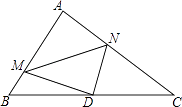 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 分解因式:x2﹣4x+4= .12. 正八边形的每个外角的度数为 .
13. 已知3是一元二次方程x2﹣4x+c=0的一个根,则方程的另一个根是 .14. 关于x的不等式组 的解集为1<x<4,则a的值为 .15. 如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,BE与CD相交于点G,且OE=OD,则AP的长为 . 16. 已知点P的坐标为(m﹣1,m2﹣2m﹣3),则点P到直线y=﹣5的最小值为 .
16. 已知点P的坐标为(m﹣1,m2﹣2m﹣3),则点P到直线y=﹣5的最小值为 .三、解答题
-
17. 计算:3tan30°﹣| |﹣ +(﹣1)2017+(﹣ )﹣2 .18. 解方程 ﹣2.
19. 体育课上,老师为了解初三女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示. (1)、求女生进球数的平均数、中位数;
(1)、求女生进球数的平均数、中位数;
(2)、投球4次,进球3个以上(含3个)为优秀,全校有初三女生400人,从中任选一位女生,求选到的女生投篮成绩为“优秀”等级的概率?20. 矩形ABCD的对角线相交于点O,AC= ,CD=1, (1)、尺规作图:作∠ABC的平分线交AD于点E,连结CE;
(1)、尺规作图:作∠ABC的平分线交AD于点E,连结CE;
(2)、判断线段BE与CE的关系,并证明你的判断.21. 如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y= (m≠0)的图象交于点A(3,1),且过点B(0,﹣2). (1)、求反比例函数和一次函数的表达式;(2)、如果点P是x轴上一点,且△ABP的面积是3,求点P的坐标.22. 如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E,F两点,连结DE,已知∠B=30°,⊙O的半径为6,弧DE的长度为2π.
(1)、求反比例函数和一次函数的表达式;(2)、如果点P是x轴上一点,且△ABP的面积是3,求点P的坐标.22. 如图,⊙O与Rt△ABC的斜边AB相切于点D,与直角边AC相交于E,F两点,连结DE,已知∠B=30°,⊙O的半径为6,弧DE的长度为2π. (1)、求证:DE∥BC;(2)、若AF=CE,求线段BC的长度.23. 甲、乙两车从A地将一批物品匀速运往B地,已知甲出发0.5h后乙开始出发,如图,线段OP、MN分别表示甲、乙两车离A地的距离S(km)与时间t(h)的关系,请结合图中的信息解决如下问题:
(1)、求证:DE∥BC;(2)、若AF=CE,求线段BC的长度.23. 甲、乙两车从A地将一批物品匀速运往B地,已知甲出发0.5h后乙开始出发,如图,线段OP、MN分别表示甲、乙两车离A地的距离S(km)与时间t(h)的关系,请结合图中的信息解决如下问题: (1)、计算甲、乙两车的速度及a的值;
(1)、计算甲、乙两车的速度及a的值;
(2)、乙车到达B地后以原速立即返回.①在图中画出乙车在返回过程中离A地的距离S(km)与时间t(h)的函数图象;
②请问甲车在离B地多远处与返程中的乙车相遇?
24. 如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC延长线上,连接AD,过B作BE⊥AD,垂足为E,交AC于点F,连接CE. (1)、求证:CF=CD;(2)、求证:DA•DE=DB•DC;(3)、探究线段AE,BE,CE之间满足的等量关系,并说明理由.25. 已知:抛物线C1:y=x2﹣2a x+2a+2 顶点P在另一个函数图象C2上(1)、求证:抛物线C1必过定点A(1,3);并用含的a式子表示顶点P的坐标;(2)、当抛物线C1的顶点P达到最高位置时,求抛物线C1解析式;并判断是否存在实数m、n,当m≤x≤n时恰有3m≤y≤3n,若存在,求出求m、n的值;若不存在,说明理由;(3)、抛物线C1和图象C2分别与y轴交于B、C点,当△ABC为等腰三角形,求a的值.
(1)、求证:CF=CD;(2)、求证:DA•DE=DB•DC;(3)、探究线段AE,BE,CE之间满足的等量关系,并说明理由.25. 已知:抛物线C1:y=x2﹣2a x+2a+2 顶点P在另一个函数图象C2上(1)、求证:抛物线C1必过定点A(1,3);并用含的a式子表示顶点P的坐标;(2)、当抛物线C1的顶点P达到最高位置时,求抛物线C1解析式;并判断是否存在实数m、n,当m≤x≤n时恰有3m≤y≤3n,若存在,求出求m、n的值;若不存在,说明理由;(3)、抛物线C1和图象C2分别与y轴交于B、C点,当△ABC为等腰三角形,求a的值.