安徽省十校联考2017年中考数学二模试卷
试卷更新日期:2017-12-07 类型:中考模拟
一、选择题
-
1. 一元二次方程5x2﹣4x﹣1=0的二次项系数和一次项系数分别为( )A、5,﹣1 B、5,4 C、5,﹣4 D、5x2 , ﹣4x2. 下列汽车标志中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 把抛物线y=﹣ 经( )平移得到y=﹣ ﹣1.A、向右平移2个单位,向上平移1个单位 B、向右平移2个单位,向下平移1个单位 C、向左平移2个单位,向上平移1个单位 D、向左平移2个单位,向下平移1个单位4. 一个直角三角形的两条直角边长的和为20cm,其中一直角边长为xcm,面积为ycm2 , 则y与x的函数的关系式是( )A、y=10x﹣ x2 B、y=10x C、y= ﹣x D、y=x(10﹣x)5. 如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是( )
3. 把抛物线y=﹣ 经( )平移得到y=﹣ ﹣1.A、向右平移2个单位,向上平移1个单位 B、向右平移2个单位,向下平移1个单位 C、向左平移2个单位,向上平移1个单位 D、向左平移2个单位,向下平移1个单位4. 一个直角三角形的两条直角边长的和为20cm,其中一直角边长为xcm,面积为ycm2 , 则y与x的函数的关系式是( )A、y=10x﹣ x2 B、y=10x C、y= ﹣x D、y=x(10﹣x)5. 如图,已知⊙O的半径为13,弦AB长为24,则点O到AB的距离是( )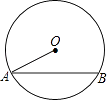 A、6 B、5 C、4 D、36. 近几年,我国经济高速发展,但退休人员待遇持续偏低,为了促进社会公平,国家决定大幅增加退休人员退休金.企业退休职工李师傅2012年月退休金为1500元,2014年达到2160元.设李师傅的月退休金从2012年到2014年年平均增长率为x,则可列方程为( )
A、6 B、5 C、4 D、36. 近几年,我国经济高速发展,但退休人员待遇持续偏低,为了促进社会公平,国家决定大幅增加退休人员退休金.企业退休职工李师傅2012年月退休金为1500元,2014年达到2160元.设李师傅的月退休金从2012年到2014年年平均增长率为x,则可列方程为( )
A、1500(1+x)2=2160 B、1500(1+x)2=2060 C、1500+1500(1+x)+1500(1+x)2=2160 D、1500(1+x)=21607. 学校早上8时上第一节课,45分钟后下课,这节课中分针转动的角度为( )A、45° B、90° C、180° D、270°8. 如图,在⊙O中,半径OC⊥弦AB于P,且P为OC的中点,则∠BAC的度数是( ) A、45° B、60° C、25° D、30°9. 二次函数y=ax2+bx+c的图象如图所示,关于此二次函数有以下四个结论:①a<0;②c>0;③b2﹣4ac>0;④ab>0,其中正确的有( )个.
A、45° B、60° C、25° D、30°9. 二次函数y=ax2+bx+c的图象如图所示,关于此二次函数有以下四个结论:①a<0;②c>0;③b2﹣4ac>0;④ab>0,其中正确的有( )个.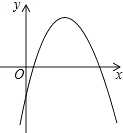 A、1 B、2 C、3 D、410. 如图,边长为2a的等边三角形ABC中,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接HN.则在点M运动过程中,线段HN长度的最小值是( )
A、1 B、2 C、3 D、410. 如图,边长为2a的等边三角形ABC中,M是高CH所在直线上的一个动点,连接MB,将线段BM绕点B逆时针旋转60°得到BN,连接HN.则在点M运动过程中,线段HN长度的最小值是( )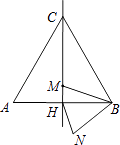 A、 a B、a C、 D、
A、 a B、a C、 D、二、填空题
-
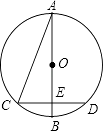
11. 关于x的一元二次方程(a﹣1)x2+x+(a2﹣1)=0的一个根是0,则a的值是12. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,连接AC.若∠CAB=22.5°,CD=6cm,则⊙O的半径为 cm.
 13. 如图,抛物线y1=(x﹣2)2﹣1与直线y2=x﹣1交于A、B两点,则当y2≥y1时,x的取值范围为 .
13. 如图,抛物线y1=(x﹣2)2﹣1与直线y2=x﹣1交于A、B两点,则当y2≥y1时,x的取值范围为 .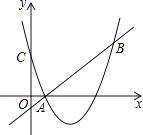
三、解答题
-
14. 解方程:4x2﹣12x+5=0.15. 已知二次函数图象经过点A(﹣3,0)、B(1,0)、C(0,﹣3),求此二次函数的解析式.
四、解答题
-
16. 如图,已知△ABC的顶点A,B,C的坐标分别是A(﹣1,﹣1),B(﹣4,﹣3),C(﹣4,﹣1).
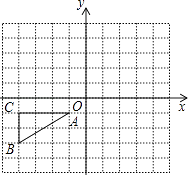
①作出△ABC关于原点O中心对称的图形;
②将△ABC绕原点O按顺时针方向旋转90°后得到△A1B1C1 , 画出△A1B1C1 , 并写出点A1的坐标.
17. 已知函数y=x2﹣mx+m﹣2.求证:不论m为何实数,此二次函数的图象与x轴都有两个不同交点.五、解答题
-
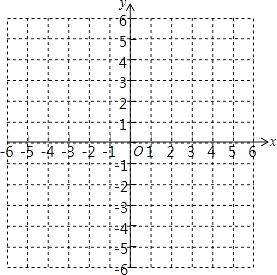
18. 已知抛物线y=﹣x2+2x+2(1)、求该抛物线的对称轴、顶点坐标以及y随x变化情况;(2)、在如图的直角坐标系内画出该抛物线的图象.
 19. 如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.
19. 如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC.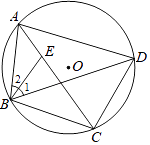 (1)、若∠CBD=39°,求∠BAD的度数;(2)、求证:∠1=∠2.
(1)、若∠CBD=39°,求∠BAD的度数;(2)、求证:∠1=∠2.六、解答题
-
20. 在如图中,每个正方形由边长为1的小正方形组成:
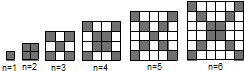 (1)、观察图形,请填写下列表格:
(1)、观察图形,请填写下列表格:正方形边长
1
3
5
7
…
n(奇数)
黑色小正方形个数
正方形边长
2
4
6
8
…
n(偶数)
黑色小正方形个数
(2)、在边长为n(n≥1)的正方形中,设黑色小正方形的个数为P1 , 白色小正方形的个数为P2 , 问是否存在偶数n,使P2=5P1?若存在,请写出n的值;若不存在,请说明理由.七、解答题
-
21. 某经销商销售一种产品,这种产品的成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量y(千克)与销售价x(元/千克)之间的函数关系如图所示:
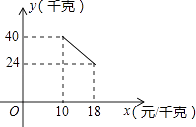 (1)、求y与x之间的函数关系式,并写出自变量x的取值范围;(2)、求每天的销售利润W(元)与销售价x(元/千克)之间的函数关系式.当销售价为多少时,每天的销售利润最大?最大利润是多少?(3)、该经销商想要每天获得150元的销售利润,销售价应定为多少?
(1)、求y与x之间的函数关系式,并写出自变量x的取值范围;(2)、求每天的销售利润W(元)与销售价x(元/千克)之间的函数关系式.当销售价为多少时,每天的销售利润最大?最大利润是多少?(3)、该经销商想要每天获得150元的销售利润,销售价应定为多少?八、解答题
-
22. 如图,已知四边形ABCD是正方形,△AEF是等边三角形,E,F分别位于DC边和BC边上.
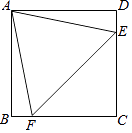 (1)、求∠DAE的度数;(2)、若正方形ABCD的边长为1,求等边三角形AEF的面积;(3)、将△AEF绕着点E逆时针旋转m(0<m<180)度,使得点A落在正方形ABCD的边上,求m的值.
(1)、求∠DAE的度数;(2)、若正方形ABCD的边长为1,求等边三角形AEF的面积;(3)、将△AEF绕着点E逆时针旋转m(0<m<180)度,使得点A落在正方形ABCD的边上,求m的值.
-
-