浙教版（2024）数学七年级上册期中模拟测试卷 A

试卷更新日期：2024-10-26 类型：期中考试

进入出卷网下载

一、单选题（每题3分，共30分）

1. $- \frac{1}{8}$ 的立方根为（　　）

A、 $- \frac{1}{2}$ B、 $\frac{1}{2}$ C、 $\pm \frac{1}{2}$ D、 $\pm \frac{\sqrt{2}}{4}$

查看试题解析
2. 预防和控制新冠肺炎最有效的办法就是接种疫苗.截止2021年12月1日，某市累计接种新冠病毒疫苗超过350万剂次，用科学记数法表示350万为（）

A、35×10⁵ B、3.5×10⁵ C、3.5×10⁶ D、3.5×10⁷

查看试题解析
3. 下列说法中正确的是（）

A、立方根等于本身的数是0 B、无限小数都是无理数 C、数轴上的所有点都表示有理数 D、 $\sqrt[3]{- m} = - \sqrt[3]{m}$

查看试题解析
4. 下面算式与 $5 \frac{1}{2} - \frac{1}{3} + 2 \frac{1}{4}$ 的值相等的是（）

A、 $3 \frac{1}{2} - (- 2 \frac{1}{3}) + (- 4 \frac{1}{4})$ B、 $\frac{1}{2} - (- 3 \frac{1}{3}) + 3 \frac{1}{4}$ C、 $2 \frac{1}{2} + (- 2 \frac{1}{3}) + 7 \frac{1}{4}$ D、 $4 \frac{1}{2} - (- \frac{1}{3}) + 3 \frac{1}{4}$

查看试题解析
5. 如图，数轴上E、F、G、H四点对应着四个连续整数，分别是e、f、g、h，且 $e + f$ $+ g + h = - 2$ ，那么原点的位置应该是（）

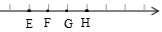A、点E B、点F C、点G D、点H

查看试题解析

二、填空题（每题4分，共24分）

6. 如果m是最大的负整数，n是绝对值最小的有理数，c是倒数等于它本身的自然数，那么代数式 $m^{2019} + 2020 n + c^{2021}$ 的值为.

查看试题解析
7. 用扑克牌中的数字牌做算“24”点游戏，抽出的四张牌分别表示7， $- 3$ ，3， $- 7$ （每张牌只能用一次，可以用加.减.乘.除等运算）请写出一个算式，使运算结果为24：.

查看试题解析

三、解答题（共8题，共72分）

8. 计算：

(1)、 $(\frac{1}{9} + \frac{1}{6} - \frac{1}{4}) \times (- 36)$ ；

(2)、 $- 1^{4} - (1 - 0.5) \times \frac{1}{3} \times | 1 - (- 5)^{2} | .$

查看试题解析
9. 计算： $\sqrt[3]{- 8} + \sqrt{9} + | 1 - \sqrt{2} | + 2 \sqrt{\frac{1}{4}}$ .

查看试题解析
10. 计算：
$- 2^{2} \times 2 + \sqrt{36} \times (\frac{1}{3} - \frac{1}{2}) - \sqrt[3]{27} \div (- 1 \frac{1}{2})$

查看试题解析
11. 阅读下列材料：
点A、B在数轴上分别表示两个数a、b ， A、B两点间的距离记为|AB|，O表示原点．当A、B两点中有一点在原点时，不妨设点A为原点，如图1，则|AB|=|OB|=|b|=|a-b|；当A、B两点都不在原点时，

①如图2，若点A、B都在原点的右边时，|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|；

②如图3，若点A、B都在原点的左边时，|AB|=|OB|-|OA|=|b|-|a|=-b-（-a）=|a-b|；

③如图4，若点A、B在原点的两边时，|AB|=|OB|+|OA|=|b|+|a|=-b+a=|a-b|．

回答下列问题：

(1)、综上所述，数轴上A、B两点间的距离为|AB|= ．

(2)、若数轴上的点A表示的数为3，点B表示的数为-4，则A、B两点间的距离为；

(3)、若数轴上的点A表示的数为x ，点B表示的数为-2，则|AB|= ，若|AB|=3，则x的值为．

查看试题解析
12. 教材上有这样一个合作学习活动：如图1，依次连结2×2方格四条边的中点A ， B ， C ， D ，得到一个阴影正方形．设每一小方格的边长为1，得到阴影正方形面积为2．

(1)、【基础尝试】：
发现图1这个阴影正方形的边长就是小方格的对角线长，则小方格对角线长是，由此我们得到一种在数轴上找到无理数的方法；

(2)、【画图探究】：
如图2，以1个单位长度为边长画一个正方形，以数字1所在的点为圆心，正方形的对角线为半径画弧，与数轴交于M ， N两点，则点M表示的数为；

(3)、【问题解决】：
如图3，3×3网格是由9个边长为1的小方格组成．
①画出面积是5的正方形，使它的顶点在网络的格点上；
②请借鉴（2）中的方法在数轴上找到表示实数 $\sqrt{5} - 1$ 的准确位置．（保留作图痕迹并标出必要线段长）

查看试题解析
13. 阅读下列信息材料：
信息1：因为无理数是无限不循环小数，因此无理数的小数部分我们不可能全部地写出来比如： $π$ 、 $\sqrt{2}$ 等，而常用的“ $\dots$ ”或者“ $\approx$ ”的表示方法都不够百分百准确；
信息2：2.5的整数部分是2，小数部分是0.5，可以看成2.5-2得来的；
信息3：任何一个无理数，都可以夹在两个相邻的整数之间，如 $2 < \sqrt{5} < 3$ ，是因为 $\sqrt{4} < \sqrt{5} < \sqrt{9}$ ；
根据上述信息，回答下列问题：

(1)、 $\sqrt{13}$ 的整数部分是，小数部分是；

(2)、若 $21 < a < 22$ ，则 $a$ 的整数部分是；小数部分可以表示为；

(3)、 $10 + \sqrt{3}$ 也是夹在相邻两个整数之间的，可以表示为 $a < 10 + \sqrt{3} < b$ 则 $a + b =$ ；

(4)、若 $\sqrt{30} - 3 = x + y$ ，其中 $x$ 是整数，且 $0 < y < 1$ ，请求 $x - y$ 的相反数.

查看试题解析