【培优卷】第三章 图形的初步认识 ——华师大版数学七年级上册
试卷更新日期:2024-10-26 类型:单元试卷
一、选择题:每题4分,共48分
-
1. 下列四个图形中,经过折叠可以围成一个棱柱的是( )A、
 B、
B、 C、
C、 D、
D、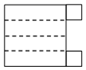 2. 如图是一个由相同小正方体搭成的几何体俯视图,小正方形中的数字表示在该位置上的小正方体的个数,则这个几何题的主视图是 ( )
2. 如图是一个由相同小正方体搭成的几何体俯视图,小正方形中的数字表示在该位置上的小正方体的个数,则这个几何题的主视图是 ( ) A、
A、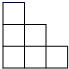 B、
B、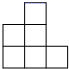 C、
C、 D、
D、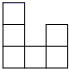 3. 一个由五个方块搭成的立体图形,从正面看是
3. 一个由五个方块搭成的立体图形,从正面看是 , 从左面看是
, 从左面看是 , 它可以是( )。 A、
, 它可以是( )。 A、 B、
B、 C、
C、 D、
D、 4. 把图1所示的正方体的展开图围成正方体(文字露在外面),再将这个正方体按照图2,依次翻滚到第1格,第2格,第3格,第4格,此时正方体朝上一面的文字为( )
4. 把图1所示的正方体的展开图围成正方体(文字露在外面),再将这个正方体按照图2,依次翻滚到第1格,第2格,第3格,第4格,此时正方体朝上一面的文字为( )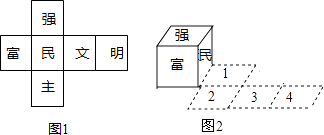 A、富 B、强 C、文 D、民5.
A、富 B、强 C、文 D、民5.如图是一个切去了一个角的正方体纸盒,切面与棱的交点A,B,C均是棱的中点,现将纸盒剪开展成平面,则展开图不可能是( )
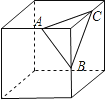 A、
A、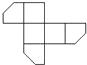
B、
B、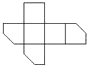
C、
C、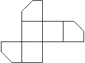
D、
D、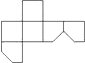
6. 下列四张正方形硬纸片,分别将阴影部分剪去后,再沿虚线折叠,其中可以围成一个封闭长方体包装盒的是( )
6. 下列四张正方形硬纸片,分别将阴影部分剪去后,再沿虚线折叠,其中可以围成一个封闭长方体包装盒的是( )
A、 B、
B、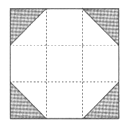 C、
C、 D、
D、 7. 下列四个生活、生产现象中,其中可用“两点之间,线段最短”来解释的现象有( )
7. 下列四个生活、生产现象中,其中可用“两点之间,线段最短”来解释的现象有( )①用两个钉子就可以把木条固定在墙上②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线③从A地到B地架设电线,总是尽可能沿着直线架设④把弯曲的公路改直,就能缩短路程.
A、①② B、①③ C、②④ D、③④8. 已知线段 , 延长至点 , 使 , 点 , 分别为线段 , 的中点,则的长度为( )A、2cm B、3cm C、5cm D、1cm或5cm9. 将一副三角尺按不同方式摆放,下列摆放方式中与一定相等的是( )A、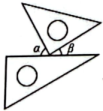 B、
B、 C、
C、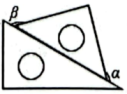 D、
D、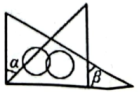 10. 如图,射线的方向是北偏东 , 射线的方向是北偏西 , 已知射线平分 , 则射线的方向是( )
10. 如图,射线的方向是北偏东 , 射线的方向是北偏西 , 已知射线平分 , 则射线的方向是( )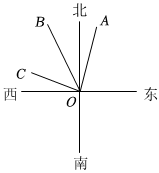 A、北偏西 B、西偏北 C、北偏西 D、西偏北11. 小亮正确完成了以下两道作图题:①“延长线段AB到C,使BC=AB“;②“反向延长线段DE到F,使点D是线段EF的一个三等分点”.针对小亮的作图,小莹说:“点B是线段AC中点”.小轩说:“DE=2DF”.下列说法正确的是( )A、小莹、小轩都对 B、小莹不对,小轩对 C、小莹、小轩都不对 D、小莹对,小轩不对12. 如图,C,D在线段BE上,下列四个说法:
A、北偏西 B、西偏北 C、北偏西 D、西偏北11. 小亮正确完成了以下两道作图题:①“延长线段AB到C,使BC=AB“;②“反向延长线段DE到F,使点D是线段EF的一个三等分点”.针对小亮的作图,小莹说:“点B是线段AC中点”.小轩说:“DE=2DF”.下列说法正确的是( )A、小莹、小轩都对 B、小莹不对,小轩对 C、小莹、小轩都不对 D、小莹对,小轩不对12. 如图,C,D在线段BE上,下列四个说法: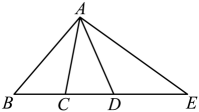
①直线上以B,C,D,E为端点的线段共有6条;②图中有3对互为补角的角;③若 , 则以A为顶点的所有小于平角的角的度数和为370°;④若BC=4,CD=3,DE=5,点F是线段BE上任意一点(包含端点),则点F到点B,C,D,E的距离之和的最小值为15,最大值为23.
其中正确说法的个数是( )
A、1个 B、2个 C、3个 D、4个二、填空题:每题4分,共24分
-
13. 若一个直四棱柱的底面是边长为2cm的正方形,侧棱长为4cm,则这个直四棱柱的所有棱长之和是cm.14. 如图,由几个相同的小正方体堆成的一个几何体,其从正面看和从上面看到的图形如图所示,若堆成的这个几何体的小正方形个数最小值a , 最大值为b , 那么 .

 15. 图所示是一个正方体的表面展开图,且相对两个面表示的整式的和都相等.如果 , 那么F所代表的整式是 .
15. 图所示是一个正方体的表面展开图,且相对两个面表示的整式的和都相等.如果 , 那么F所代表的整式是 . 16. 在同一直线上有 , , , 不重合的四个点, , , , 则的长为 .17. 如图,点是量角器的中心点,射线经过刻度线 . 若 . 射线、分别经过刻度线和 , 在刻度线的右侧.下列结论:①;②若与互补,则射线经过刻度线;③若 , 则图中共有6对角互为余角.其中正确的是(填序号).
16. 在同一直线上有 , , , 不重合的四个点, , , , 则的长为 .17. 如图,点是量角器的中心点,射线经过刻度线 . 若 . 射线、分别经过刻度线和 , 在刻度线的右侧.下列结论:①;②若与互补,则射线经过刻度线;③若 , 则图中共有6对角互为余角.其中正确的是(填序号). 18. 如图,点O在直线AB上,从点O引出射线OC,其中射线OD平分∠AOC,射线OE平分∠BOC,下列结论:
18. 如图,点O在直线AB上,从点O引出射线OC,其中射线OD平分∠AOC,射线OE平分∠BOC,下列结论:
①∠DOE=90°;
②∠COE与∠AOE互补;
③若OC平分∠BOD,别∠AOE=150°;
④∠BOE的余角可表示为 .
其中正确的是 . (只填序号)
三、作图题(共3题,共26分)
-
19. 图1所示的三棱柱,高为8cm,底面是一个边长为5cm的等边三角形.
 (1)、这个三棱柱有条棱,有个面;(2)、图2框中的图形是该三棱柱的一种表面展开图的一部分,请将它补全(一种即可);(3)、要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,至少需剪开条棱,需剪开棱的棱长的和的最大值为cm.20. 在平整的地面上,有若干个完全相同棱长的小正方体堆成一个几何体,如图所示.
(1)、这个三棱柱有条棱,有个面;(2)、图2框中的图形是该三棱柱的一种表面展开图的一部分,请将它补全(一种即可);(3)、要将该三棱柱的表面沿某些棱剪开,展开成一个平面图形,至少需剪开条棱,需剪开棱的棱长的和的最大值为cm.20. 在平整的地面上,有若干个完全相同棱长的小正方体堆成一个几何体,如图所示.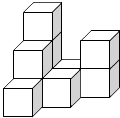 (1)、请画出这个几何体的三视图.(2)、如果在这个几何体的表面喷上黄色的漆,则在所有的小正方体中,有个正方体只有一个面是黄色,有个正方体只有两个面是黄色,有个正方体只有三个面是黄色.(3)、若现在你手头还有一些相同的小正方体,如果保持俯视图和左视图不变,最多可以再添加几个小正方体?
(1)、请画出这个几何体的三视图.(2)、如果在这个几何体的表面喷上黄色的漆,则在所有的小正方体中,有个正方体只有一个面是黄色,有个正方体只有两个面是黄色,有个正方体只有三个面是黄色.(3)、若现在你手头还有一些相同的小正方体,如果保持俯视图和左视图不变,最多可以再添加几个小正方体?
21. 如图,在同一平面内有三个点A , B , C . (1)、利用尺规,按下面的要求作图.(要求:不写画法,保留作图痕迹)
(1)、利用尺规,按下面的要求作图.(要求:不写画法,保留作图痕迹)①作射线AB;
②作线段BC;
③连接AC , 并在线段AC上作一条线段AD , 使AD=AB , 连接BD .
(2)、观察(1)题得到的图形,请直接写出BD+DC与BC的大小关系是 , 依据的数学原理是 .四、综合题(共5题,共52分)
-
22. 【问题情境】小明所在的综合实践小组准备制作一些无盖纸盒收纳班级讲台上的粉笔.
【操作探究】
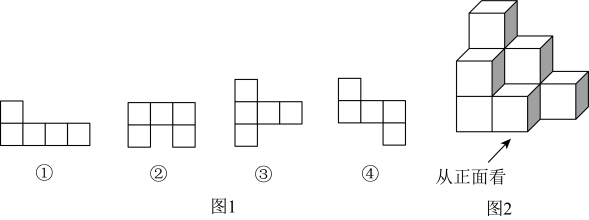
(1)、图1中的第个图形经过折叠不能围成无盖正方体纸盒(填序号).(2)、小圣所在的综合实践小组把折叠成9个棱长都为的无盖正方体纸盒摆成如图2所示的几何体.①请计算出这个几何体的表面积;
②要保持从上面看到的平面图形不变,最多可以拿走小正方体的个数是 ▲ .
23. 综合与实践(1)、问题情境:数学活动课上,王老师出示了一个问题:
如图1,已知线段 , 点C在线段上, , 点P在线段上, . 求的长.

请解答王老师提出的问题.
(2)、实践探究:王老师改变条件,并提出新问题,点P在的延长线上时,原题的其他条件不变,求的长.

知识迁移:
数学活动小组同学把上述线段问题改为角研究之后发现,也能提出类似问题.
该小组提出下面的问题,请你解答.
(3)、如图3,已知 , 射线在的内部, , 射线在平面内, . 请直接写出的度数.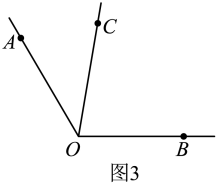 24. 【新知理解】
24. 【新知理解】点C在线段上,若或 , 则称点C是线段的“优点”,线段 , 称作互为“优点”伴侣线段.

例如,图1,线段的长度为6,点C在上,的长度为2,则点C是线段的其中一个“优点”.
(1)若点C为图1中线段的“优点” , 则______;
(2)若点D也是图1中线段的“优点”(不同于点C),则______(填“”或“”)
【解决问题】

如图2,数轴上有E,F两点,其中E点表示的数为1,F点表示的数为4;
(3)若M点在N点的左侧,且M,N均为线段的“优点”,求线段的长;
(4)若点G在线段的延长线上,且线段与互为“优点”伴侣线段,求点G表示的数.
25. 如图 (1)、【特例感知】如图 , 已知线段 , , 点和点分别是 , 的中点若 , 则;(2)、【知识迁移】我们发现角的很多规律和线段一样,如图 , 已知在内部转动,射线和射线分别平分和;
(1)、【特例感知】如图 , 已知线段 , , 点和点分别是 , 的中点若 , 则;(2)、【知识迁移】我们发现角的很多规律和线段一样,如图 , 已知在内部转动,射线和射线分别平分和;若 , , 求的度数;
请你猜想 , 和三个角有怎样的数量关系?请说明理由.
(3)、【类比探究】如图 , 在内部转动,若 , , , , 求的度数用含有的式子表示计算结果 .26. 操作与实践:在综合与实践活动课上,老师将一副三角板按图1所示的位置摆放,分别在∠AOC,∠BOD的内部作射线OM,ON,然后提出如下问题:先添加一个适当条件,再求∠MON的度数.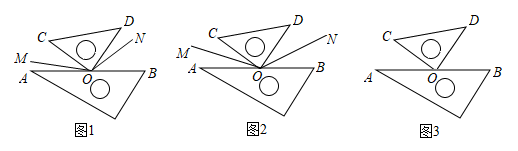 (1)、特例探究:“兴趣小组”的同学添加了:“若OM,ON分别平分∠AOC,∠BOD”,画出如图2所示图形.小组3号同学佳佳的做法:由于图中∠AOC与∠BOD的和为90°,所以我们容易得到∠MOC与∠NOD的和,这样就能求出∠MON的度数.请你根据佳佳的做法,写出解答过程.(2)、特例探究:“发现小组”的同学添加了:“若∠MOC=∠AOC,∠DON=∠BOD”,画出如图3所示图形.小组2号同学乐乐的做法:设∠AOC的度数为x°,我们就能用含有x°的式子表示出∠COM和∠DON的度数,这样就能求出∠MON的度数,请你根据乐乐的做法,写出解答过程.(3)、类比拓展:受“兴趣小组”和“发现小组”的启发,“创新小组”的同学添加了:“若∠MOC=∠AOC,∠DON=∠BOD”.请你直接写出∠MON的度数.
(1)、特例探究:“兴趣小组”的同学添加了:“若OM,ON分别平分∠AOC,∠BOD”,画出如图2所示图形.小组3号同学佳佳的做法:由于图中∠AOC与∠BOD的和为90°,所以我们容易得到∠MOC与∠NOD的和,这样就能求出∠MON的度数.请你根据佳佳的做法,写出解答过程.(2)、特例探究:“发现小组”的同学添加了:“若∠MOC=∠AOC,∠DON=∠BOD”,画出如图3所示图形.小组2号同学乐乐的做法:设∠AOC的度数为x°,我们就能用含有x°的式子表示出∠COM和∠DON的度数,这样就能求出∠MON的度数,请你根据乐乐的做法,写出解答过程.(3)、类比拓展:受“兴趣小组”和“发现小组”的启发,“创新小组”的同学添加了:“若∠MOC=∠AOC,∠DON=∠BOD”.请你直接写出∠MON的度数.