【基础卷】第三章 图形的初步认识 单元测试 ——华师大版（2024）数学七年级上册
试卷更新日期：2024-10-26 类型：单元试卷
一、选择题：每题4分，共48分
-
1. 下列几何体中，属于棱柱的是（ ）A、
B、
C、
D、
2. 鲁班锁，民间也称作孔明锁、八卦锁，它起源于中国古代建筑中首创的榫卯结构．如图是鲁班锁的其中一个部件，从正面看到的平面图形是（ ）
A、
B、
C、
D、
3. 下列现象属于中心投影的有（ ）①小孔成像； ②皮影戏；③手影； ④放电影.
A、1个 B、2个 C、3个 D、4个4. 如图是某一物体的三视图，则此三视图对应的物体是（ ）
A、
B、
C、
D、
5. 下列图形中，为四棱锥的侧面展开图的是（ ）A、
B、
C、
D、
6. 长方形剪去一个角后所得的图形一定不是（ ）A、五边形 B、梯形 C、长方形 D、三角形7. 走马灯，又称仙音烛，据史料记载，走马灯的历史起源于隋唐时期，盛行于宋代，是中国特色工艺品，常见于除夕、元宵、中秋等节日，在一次综合实践活动中，一同学用如图所示的纸片，沿折痕折合成一个棱锥形的“走马灯”，正方形做底，侧面有一个三角形面上写了“祥”字，当灯旋转时，正好看到“吉祥如意”的字样.则在A、B、C处依次写上的字可以是( )
A、吉如意 B、意吉如 C、吉意如 D、意如吉8. 值日生每天值完日后，总是先把每一列最前和最后的课桌摆好，然后再依次摆中间的课桌，很快就能把课桌摆得整整齐齐，他们这样做的道理是（ ）A、两点之间，线段最短 B、两点确定一条直线 C、垂线段最短 D、以上说法都不对9. 两根木条，一根长另一根长将它们一端重合且放在同一直线上，此时两根木条的中点之间的距离为（ ）A、 B、 C、或 D、点或10. 观察站测得一轮船在北偏东 ， 则在轮船上看观察站的方位是（ ）A、南偏东 B、南偏西 C、南偏东 D、南偏西11. 下图中用量角器测得的度数是（ ）
A、 B、 C、 D、12. 如图，点在直线上， ， 下列说法错误的是（ ）
A、 B、与互余 C、与互补 D、与互补二、填空题：每题4分，共24分
-
13. 在一个棱柱中，一共有 个面，则这个棱柱有条棱.14. 一个小立方体的六个面分别标有数字1、2. 3、4、5、6，从三个不同的方向看到的情形如图所示，则数字6的对面是.
15. 如图是一个正方体的展开图，该正方体展开前，“核”字对面的字是 ．
16. 将如图形状的纸片折叠，可以围成的几何体的名称是 ， 与面对应的是面.
17. 如图，从长春站去往胜利公园，与其它道路相比，走人民大街路程最近，其蕴含的数学道理是 ．
18. 如果一个角的补角是150°，那么这个角的余角的度数是三、作图题：共3题，共30分
-
19. 观察如图所示的几何体，已知小正方体的棱长为1．
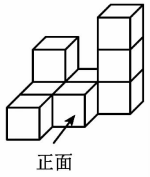(1)、该几何体的体积为；(2)、请在下面网格中分别画出你从正面、左面、上面所看到的几何体的形状图．
从正面看 从左面看 从上面看20. 已知平面上的三个点、、和直线 ， 根据要求画图．
画射线；
确定点的位置，使得点既在直线上，又在直线上；
在直线上确定点的位置，使得点到点与点的距离之和最小．21. 如图，已知∠α和∠β，用直尺和圆规作∠ABC，使∠ABC=∠α-∠β．
四、解答题：共4题，共48分
-
22. 如图所示的五棱柱的底面边长都是5cm，侧棱长12cm，它有多少个面？它有多少条棱?它有多少个顶点?它的所有侧面的面积之和是多少？
23. 如图是一个正方体的表面展开图，若正方体中相对的面上的数互为相反数，则、x、y的值分别为多少？
