【培优卷】3.5最基本的图形—点和线 同步练习——华师大版（2024）数学七年级上册
试卷更新日期：2024-10-25 类型：同步测试
一、复习巩固
-
1. 下列说法，正确的是（ ）A、经过一点有且只有一条直线 B、两点确定一条直线 C、两条直线相交至少有两个交点 D、线段 就是表示点A到点B的距离2. 下面说法与所示的几何图形相符的是（ ）
A、点在直线上 B、直线和直线表示同一条直线 C、点在射线上 D、直线与直线都经过点3. 下列四个生活中的现象：①用两个钉子就可以把木条固定在墙上；②植树时，只要确定两棵树的位置，就能确定这一行树所在的直线；③从地到地架设电线，总是尽可能沿着线段方向架设；④把弯曲的公路改直，就能缩短路程．其中可以用基本事实“两点确定一条直线”来解释的有（ ）A、①② B、①③ C、②③ D、③④4. “如图是一个正方形，把此正方形沿虚线AB减去一个角，得到一个五边形，则这个五边形的周长____原来正方形的周长，理由是____”此题中横线上应填写的正确答案是（ ）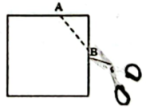
A、大于，两点之间线段最短 B、小于，两点之间线段最短 C、大于，垂线段最短 D、小于，垂线段最短5. 如图，已知四条线段 ， ， ， 中的一条与挡板另一侧的线段 在同一直线上，请借助直尺判断该线段是（ ）
A、 B、 C、 D、6. 如果A，B，C在同一条直线上，线段AB＝6cm，BC＝2cm，则A、C两点间的距离是（ ）A、8cm B、4cm C、8cm或4cm D、无法确定7. 点 ， ， 在同一直线上，已知 ， ， 则线段的长是（ ）A、2cm B、3cm C、2cm或5cm D、3cm或5cm8. 已知线段 ， ， 且A，B，C三点在同一直线上，则线段AC的长度为（ ）A、1cm B、1cm或9cm C、2cm或8cm D、9cm9. “世界桥梁看中国，中国桥梁看贵州”．右图是贵州一座横跨峡谷的大桥，天堑变通途，径直的大桥极大程度地缩短了大桥两端的路程，其中“径直的大桥缩短了大桥两端的路程”所蕴含的数学原理是.
10. 在日常生活和生产中有很多现象可以用数学知识进行解释．如图，要把一根挂衣帽的挂钩架水平固定在墙上，至少需要钉个钉子．用你所学数学知识说明其中的道理 ．
11. 平面上有四个点 ， 按照以下要求作图（保留作图痕迹）：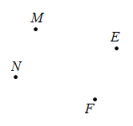
(1)、连接 ， 并延长至G，使；(2)、作射线；(3)、作直线 ， 并在直线MF上确定点H，使得最短．12. 已知线段 ， 如图所示，根据下列要求，依次画图或计算．
(1)、根据下列步骤画图，并用含有 ， 的式子表示线段 ．①作出射线；
②在射线上依次截取；
③在线段上截取 ．
(2)、若 ， ， 是线段的中点，求线段的长．13. 如图，在直线上作线段 ， 再在线段上作线段 ．
(1)、用含的式子表示出线段的长；(2)、若M是的中点，N是的中点，求线段的长．二、能力提升
-
14. 在一条线段中间另有个点，则这个点可以构成（ ）条线段．A、 B、 C、 D、15. 已知线段 ， 点C为线段AB的中点，点D为线段AC上的三等分点，则线段BD的长的最大值为（ ）
A、16 B、18 C、15 D、2016. 下列说法中不正确的是（ ）A、若点C在线段AB的延长线上，则AC>AB B、若点C在线段AB上，则AC<AB C、若点C在直线AB上，则AC>AB D、若A，B，C三点不在一条直线上，可能AC=AB17. 线段 ， C为线段AB的中点，点D在直线AB上，若 ， 则CD＝ ．18. 2023年5月9日，湖南湘江新区大王山欢乐云巴正式对外运营. 一张云巴票就能领略沿途10余个景点，感受大王山人文风情.如图，乘云巴从山塘站出发，沿途经过7个车站方可到达观音港站，那么运营公司在山塘站，观音港站两站之间需要安排不同的车票种.
19. 如图，在数轴上有A，B，C，D四个点，且2AB=BC=3CD，若A，D两点表示的数分别为-5，6，点E为BD的中点，则该数轴上点E表示的数是.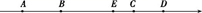
20. 如图，点P是线段上的一点，点M、N分别是线段的中点．
(1)、如图1，若点P是线段的中点，且 ， 则线段的长 ， 线段的长；(2)、如图2，若点P是线段上的任一点，且 ， 求线段的长；(3)、若点P是直线上的任意一点，且 ， 直接写出线段的长．三、拓广探索
-
21. 如图，将一段长为100cm绳子AB拉直铺平后折叠（绳子无弹性，折叠处长度忽略不计），使绳子与自身一部分重叠．若将绳子AB沿N点折叠后，点B落在处（点始终在点A右侧），在重合部分上沿绳子垂直方向剪断，将绳子分为三段，若这三段的长度由短到长的比为2∶3∶5，BN的值可能为 ．
22. 如图
(1)、【观察思考】如图线段AB上有两个点C、D，分别以点A、B、C、D为端点的线段共有条(2)、【模型构建】若线段上有m个点（包括端点），则该线段上共有条线段(3)、【拓展应用】若有8位同学参加班级的演讲比赛，比赛采用单循环制（即每两位同学之间都要进行一场比赛），请你应用上述模型构建，求一共要进行多少场比赛？23. 用叠合法比较线段的长短是度量线段长度的基本原理．根据这个原理，以及线段的和差的意义，我们可以得到一些简易的测量线段长的方法．
如图，如果我们没有带合适的测量工具，那么用我们身体的“尺子”来测量不失为好方法．然而每个人“1拇”，“1肘”，“1柞”的长度不尽相同，所以测量者可先测量出自己的“1拇”，“1肘”和“1柞”究竟有多长．
现在我们来进行以下实践活动：
①与同伴合作，用刻度尺测量每人的“1拇”，“1肘”，“1柞”的长度．
②分别选择我们身体中的“尺子”测量数学课本的长与宽，课桌的长、宽、高，教室中黑板的长与宽等．再用刻度尺量一量，评价上述测量的精确程度．
你的身体中还有哪些“尺子”？把你在户外使用上述测量方法的典型案例记录下来，在适当的场合与同伴交流．