【培优卷】3.4平面图形 同步练习——华师大版（2024）数学七年级上册

试卷更新日期：2024-10-25 类型：同步测试

进入 出卷网 下载

一、复习巩固

  • 1. 以下几种图形：①三角形 ②正方体 ③圆 ④圆锥 ⑤圆柱 ⑥正方形 ⑦梯形 ⑧球⑨等腰三角形，其中不属于平面图形的是（　　）

    A、②③④⑧ B、②④⑤ C、④⑤⑧⑨ D、②④⑤⑧

    查看试题解析

  • 2.

    如图所示是一间房子的平面示意图，组成这幅图的简单几何图形是（　　)

    ​

    A、三角形、长方形 B、三角形、正方形、长方形 C、三角形、正方形、长方形、梯形 D、正方形、长方形、梯形

    查看试题解析

  • 3. 下列结论，其中正确的为（　　）

    ①圆柱由3个面围成，这3个面都是平面    ②圆锥由2个面围成，这2个面中，1个是平的，1个不是平的    ③球仅由1个面围成，这1个面是平的   ④正方体由6个面围成，这6个面都是平的

    A、①② B、②③ C、②④ D、③④

    查看试题解析

  • 4. 已知一个圆，任意画出它的三条半径，能得到（　　）个扇形．

    A、4 B、5 C、6 D、8

    查看试题解析

  • 5. 从一个n边形的同一个顶点出发，分别连接这个顶点与其余各顶点，若把这个多边形分割成6个三角形，则n的值是（   ）
    A、6 B、7 C、8 D、9

    查看试题解析

  • 6. 有下列说法：

    ①由许多条线段连接而成的图形叫做多边形；

    ②多边形的边数是不小于4的自然数；

    ③从一个多边形（边数为n）的同一个顶点出发，分别连接这个顶点与其余与之不相邻的各顶点，可以把这个多边形分割成（n﹣2）个三角形；

    ④半圆是扇形．

    其中正确的结论有（   ）

    A、1个 B、2个 C、3个 D、4个

    查看试题解析

  • 7. 从n边形的一个顶点出发，连接其余各顶点，可以将这个n边形分割成17个三角形，则n＝.

    查看试题解析

  • 8.

    如图所示，写出这些多边形的名称，并从多边形的一个顶点出发到其他顶点把多边形分割成若干个三角形．

    查看试题解析

  • 9. 分别画出下列平面图形：长方形，正方形，三角形，圆．

    查看试题解析

  • 10.

    观察下图，思考问题：

    (1)、你认识上面的图片中的哪些物体？

    (2)、这些物体的表面形状类似与哪些几何体？说说你的理由。

    (3)、你能再举出一些常见的图形吗？​

    查看试题解析

二、能力提升

  • 11.

    （体验探究题）如图所示，该图中包含的平面图形有（　　）

    ①等腰梯形；②正六边形；③四边形；④三角形（实线与虚线组成）；⑤平行四边形（实线与虚线组成）

    ​

    A、3种平面图形 B、5种平面图形 C、4种平面图形 D、以上都不对

    查看试题解析

  • 12. 一个多边形最少可分割成五个三角形，则它是（    ）边形
    A、8 B、7 C、6 D、5

    查看试题解析

  • 13. 在学习完多边形后，小华同学将一个五边形沿如图所示的直线1剪掉一个角后，得到一个多边形，下列说法正确的是（ ）

    A、这个多边形是一个五边形 B、从这个多边形的顶点A出发，最多可以画4条对角线 C、从顶点A出发的所有对角线将这个多边形分成4个三角形 D、以上说法都不正确

    查看试题解析

  • 14.

    图中能数出几个长方形（正方形也算作长方形）（　　）

    A、64 B、63 C、60 D、48

    查看试题解析

  • 15.

    图中有多少个三角形？

    查看试题解析

  • 16. 七巧板又称智慧板，是中国民间流传的智力玩具，它是由七块板组成（如图1），用这七块板可拼出许多图形（1600种以上），例如：三角形、平行四边形、以及不规则的多边形，它还可以拼出各种人物、动物、建筑等．请你用七巧板中标号为①②③的三块板（如图2经过平移、旋转拼出下列图形（相邻两块板之间无空隙，无重叠；示意图的顶点画在小方块顶点上）：

    (1)、拼成长方形，在图3中画出示意图；
    (2)、拼成等腰直角三角形，在图4中面出示意图．

    查看试题解析

三、拓广探索

  • 17. 多边形边上（包括顶点）或内部的一点与多边形各顶点的连线，将多边形分割成若干个小三角形．图甲给出了四边形的三种分割方法，分别将四边形分割成了2个、3个和4个小三角形．

    (1)、请你将图乙中的六边形按这三种方法分割，并写出得到的小三角形的个数．
    (2)、若将n边形(n⩾4)按这三种方法作类似的分割，所得的小三角形个数分别是多少？

    查看试题解析

  • 18. 美国著名的数学科普作家马丁•加德纳，他的妙趣横生的科普作品《哈哈!灵机一动》让无数读者为数学着谜，下面的问题改编自马丁•加德纳的文集.

    最早的器具型趣题无疑是古代中国的七巧板（由如图1的七块板组成的，完整图案为一正方形）游戏，它可以引出一些不平凡的数学问题，例如用一副七巧板可拼出多少种凸多边形（图形均在各边所在的直线的同侧）？1942年，中国浙江大学的两位数学家王福春和熊全治，证明了用一副七巧板只能拼出13种凸多边形.

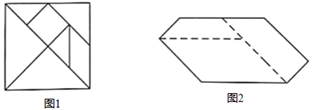
    图2中给出了其中的一种凸六边形，请你参考图1，在图2中画出七巧板中的七块.

    查看试题解析

  • 19. 七巧板(图1)是我们祖先的一项卓越创造，在19世纪曾极为流行．七巧板虽然只由7块板组成，但用它们可以拼出人、动物、交通工具等各种图形．

    (1)、从图1中，你能观察到哪些你所熟悉的图形？
    (2)、你能用七巧板拼出图2吗？
    (3)、发挥你的创造力，尽可能多地用七巧板拼出表示人或物的图案．

    查看试题解析

  • 20. 如图所示，若将类似于a、b、c、d四个图的图形称做平面图，则其顶点数、边数与区域数之间存在某种关系．观察图b和表中对应的数值，探究计数的方法并作答．

    (1)、数一数每个图中各有多少个顶点、多少条边，这些边围出多少个区域并填表：

    图

     a

    b

     c

     d

     顶点数（S）

     7

     边数（M）

     9

     区域数（N）

     3

    (2)、根据表中数值，写出平面图的顶点数、边数、区域数之间的一种关系；
    (3)、如果一个平面图有20个顶点和11个区域，那么利用（2）中得出的关系可知这个平面图有条边．

    查看试题解析