【培优版】浙教版数学八上4.2 平面直角坐标系同步练习

试卷更新日期：2024-10-24 类型：同步测试

进入出卷网下载

一、选择题

1. 第三象限内的点P到x轴的距离是7，到y轴的距离是8，那么点P的坐标是（）

A、 $(- 8, - 7)$ B、 $(- 7, - 8)$ C、 $(- 7, 8)$ D、 $(7, 8)$

查看试题解析
2. 在如图所示的平面直角坐标系中，小手盖住的点的坐标可能是（）

A、 $(- 1, 1)$ B、 $(- 1, - 1)$ C、 $(1, - 1)$ D、 $(1, 1)$

查看试题解析
3. 已知点 $P (3 a - 2, a + 6)$ 到两坐标轴的距离相等，那么 $a$ 的值为（）

A、4 B、 $- 6$ C、 $- 1$ 或4 D、 $- 6$ 或 $\frac{3}{2}$

查看试题解析
4. 在平面直角坐标系中，点 $P (| a | + 1, - 2)$ 所在的象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 下列说法正确的是（　　）

A、若ab＝0，则点P（a ， b）表示原点 B、点（2，a）在第三象限 C、若点A、B的坐标分别是（2，﹣2）、（2，2），则直线AB∥x轴 D、若ab＞0，则点P（a ， b）在第一或第三象限

查看试题解析
6. 象棋在中国有着三千多年的历史，由于用具简单，趣味性强，成为流行极为广泛的益智游戏．如图是一局象棋残局，已知表示棋子“马”和“帥”的点的坐标分别为 $(3, 2)$ ， $(- 1, - 1)$ ，则表示棋子“炮”的点的坐标为（）．

A、 $(2, 3)$ B、 $(0, 2)$ C、 $(2, 0)$ D、 $(1, 3)$

查看试题解析
7. 下列说法中，正确的是（）

A、点P（3，2）到x轴的距离是3 B、在平面直角坐标系中，点（2，－3）和点（－3，2）表示同一个点 C、若y＝0，则点M（x ， y）在y轴上 D、在平面直角坐标系中，第三象限内点的横坐标与纵坐标同号

查看试题解析
8. 若点 $P (a + 1 ， 2 - 2 a)$ 在第一象限，则 $a$ 的取值范围在数轴上表示为（）

A、 B、 C、 D、

查看试题解析

二、填空题

9. 在平面直角坐标系中，对于P（x，y）作变换得到P（﹣y+1，x+1），例如：A₁（3，1）作上述变换得到A₂（0，4），再将作上述变换得到A₃（﹣3，1），这样依次得到A₂ ， A₃ ， A₁ ， …，A₀ ， ……，则A₂₀₂₀的坐标是.

查看试题解析
10. 在平面直角坐标系xOy中，对于点P(x，y)，我们把点P′(－y＋1，x＋1)叫做点P的伴随点．已知点A₁的伴随点为A₂ ，点A₂的伴随点为A₃ ，点A₃的伴随点为A₄ ， …，这样依次得到点A₁ ， A₂ ， A₃ ， …，A_n ， ….若点A₁的坐标为(3，1)，则点A₂的坐标为，点A_{2 019}的坐标为；若点A₁的坐标为(a，b)，对于任意的正整数n，点A_n均在x轴上方，则a，b应满足的条件为．

查看试题解析
11. 如图，在平面直角坐标系中，点A₁(1，2)，A₂(2，0)，A₃(3，－2)，A₄(4，0)……根据这个规律，探究可得点A₂₀₁₇的坐标是.

查看试题解析
12. 如图，在平面直角坐标系上有个点 $A (- 1 ， 0)$ ，点A第1次向上跳动1个单位至点 $A_{1} (- 1 ， 1)$ ，紧接着第2次向右跳动2个单位至点 $A_{2} (1 ， 1)$ ，第3次向上跳动1个单位至点 $A_{3}$ ，第4次向左跳动3个单位至点 $A_{4}$ ，第5次又向上跳动1个单位至点 $A_{5}$ ，第6次向右跳动4个单位至点 $A_{6}$ ， ……，依此规律跳动下去，点A第2023次跳动至点 $A_{2023}$ 的坐标是．

查看试题解析

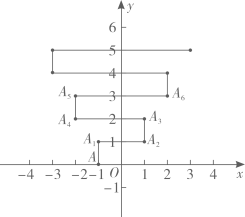
三、解答题

13. 若点 $P (x ， y)$ 的坐标满足 ${\begin{array}{l} x + y = 2 a - b - 4 \\ x - y = b - 4 \end{array}$ ．

(1)、当 $a = 1$ ， $b = 2$ 时，求点P的坐标；

(2)、若点P在第二象限，且符合要求的整数a只有四个，求b的取值范围；

(3)、若关于z的方程 $y z + x + 4 = 0$ 有唯一解 $z = 2$ ，求关于t的不等式 $a t > b$ 的解集．

查看试题解析

四、实践探究题

14. 在平面直角坐标系 $x O y$ 中，点 $A (a, b)$ ， $B (c, d)$ ，若 $c - a = d - b \neq 0$ ，则称点 $A$ 与点 $B$ 互为“等差点”，例如：点 $A (- 1, 3)$ ，点 $B (2, 6)$ ，因为 $2 - (- 1) = 6 - 3 \neq 0$ ，所以点 $A$ 与点 $B$ 互为“等差点”．

(1)、若点 $A$ 的坐标是 $(4, - 2)$ ，则在点 $B_{1} (2, 0)$ ， $B_{2} (- 1, - 7)$ ， $B_{3} (0, - 6)$ 中，点 $A$ 的“等差点”为点；

(2)、若点 $A$ 的坐标是 $(5, - 3)$ 的“等差点” $B$ 在坐标轴上，求点 $B$ 的坐标；

(3)、若点 $A$ 的坐标是 $(- \sqrt{3}, 2 m)$ 与点 $B (2 \sqrt{3}, - n)$ 互为“等差点”，且 $m$ 、 $n$ 互为相反数，求点 $B$ 的坐标．

查看试题解析

五、综合题

15. 若点P（a，a－5）到x轴的距离为 $m_{1}$ ，到y轴的距离为 $m_{2}$ ．

(1)、当a＝1时，直接写出 $m_{1} + m_{2} =$ ；

(2)、若 $m_{1} + m_{2} = 7$ ，求出点P的坐标；

(3)、若点P在第四象限，且 $2 m_{1} + k m_{2} = 10$ （k为常数），求出k的值．

查看试题解析