人教版数学九年级全册知识点训练营——正多边形与圆
试卷更新日期:2024-10-24 类型:复习试卷
一、夯实基础
-
1. 如图,五边形是正五边形,且 . 若 , 则( )
 A、 B、 C、 D、2. 如图,点 , , , 为正边形的顶点,点为正边形的中心.若 , 则( )
A、 B、 C、 D、2. 如图,点 , , , 为正边形的顶点,点为正边形的中心.若 , 则( ) A、七 B、八 C、九 D、十3. 正n边形的中心角是30°,( )A、6 B、8 C、10 D、124. 已知正六边形的周长是24,则这个正六边形的半径为 .5. 将一个正六边形绕着其中心,至少旋转度可以和原来的图形重合.6. 半径为5的圆内接正六边形的边心距为.
A、七 B、八 C、九 D、十3. 正n边形的中心角是30°,( )A、6 B、8 C、10 D、124. 已知正六边形的周长是24,则这个正六边形的半径为 .5. 将一个正六边形绕着其中心,至少旋转度可以和原来的图形重合.6. 半径为5的圆内接正六边形的边心距为.二、能力提升
-
7. 如图,正六边形内接于 , 连接 , 若 , 则正多边形的面积是( )
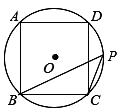
 A、 B、 C、 D、8. 如图,四边形是正方形,以B为圆心,作半径长为2的半圆,交于点E . 将半圆B绕点E逆时针旋转,记旋转角为 , 半圆B正好与边相切,则正方形的边长为( )
A、 B、 C、 D、8. 如图,四边形是正方形,以B为圆心,作半径长为2的半圆,交于点E . 将半圆B绕点E逆时针旋转,记旋转角为 , 半圆B正好与边相切,则正方形的边长为( ) A、4 B、 C、 D、39. 已知一个正多边形的内角和是外角和的2倍,则正多边形的每个内角的度数 .10. 如图,在⊙O中,AB是⊙O的内接正六边形的一边,BC是⊙O的内接正十边形的一边,则∠ABC=°.
A、4 B、 C、 D、39. 已知一个正多边形的内角和是外角和的2倍,则正多边形的每个内角的度数 .10. 如图,在⊙O中,AB是⊙O的内接正六边形的一边,BC是⊙O的内接正十边形的一边,则∠ABC=°.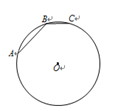 11. 如图,多边形为内接正五边形,与相切于点 , 则 .
11. 如图,多边形为内接正五边形,与相切于点 , 则 .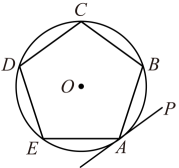 12. 如图甲所示,正五边形ABCDE内接于⊙O,阅读以下作图过程,并回答相关问题:
12. 如图甲所示,正五边形ABCDE内接于⊙O,阅读以下作图过程,并回答相关问题:作法如图乙所示.①作直径AF.②以F为圆心,FO为半径作圆弧,与⊙O交于点M,N.③连结AM,MN,NA.
 (1)、求∠ABC的度数.(2)、△AMN是正三角形吗?请说明理由.(3)、从点A开始,以DN长为半径,在⊙O上依次截取点,再依次连结这些分点,得到正n边形,求n的值.
(1)、求∠ABC的度数.(2)、△AMN是正三角形吗?请说明理由.(3)、从点A开始,以DN长为半径,在⊙O上依次截取点,再依次连结这些分点,得到正n边形,求n的值.三、拓展创新
-
13. 已知在正六边形ABCDEF中,P是EF的中点,若阴影部分四边形ABPE的面积为9,则五边形BCDEP的面积是( )
 A、12 B、 C、18 D、14. 我国古代数学家刘徽利用圆内接正多边形创立了“割圆术”,现将半径为2的圆十二等分构造出2个矩形和1个正方形(如图),则阴影部分的面积是( )
A、12 B、 C、18 D、14. 我国古代数学家刘徽利用圆内接正多边形创立了“割圆术”,现将半径为2的圆十二等分构造出2个矩形和1个正方形(如图),则阴影部分的面积是( )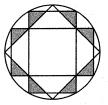 A、1 B、 C、 D、15. 如图,正方形 和正 都内接于半径为1的 , 与 、 分别相交于点 、 ,则 的长为.
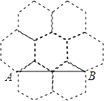
A、1 B、 C、 D、15. 如图,正方形 和正 都内接于半径为1的 , 与 、 分别相交于点 、 ,则 的长为.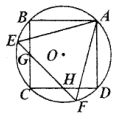 16. 蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上.设定AB边如图所示,则△ABC是直角三角形的个数有个
16. 蜂巢的构造非常美丽、科学,如图是由7个形状、大小完全相同的正六边形组成的网络,正六边形的顶点称为格点,△ABC的顶点都在格点上.设定AB边如图所示,则△ABC是直角三角形的个数有个