人教版数学九年级全册知识点训练营——四点共圆辅助圆模型
试卷更新日期:2024-10-22 类型:复习试卷
一、夯实基础
-
1. 如图,菱形ABCD中, , 点是AB边上的点, , 点是BC上的一点,是以点为直角顶点,为角的直角三角形,连结AG.当点在直线BC上运动时,线段AG的最小值是( )
 A、2 B、 C、 D、42. 如图,四边形 中, , 平分 , , ,则 的长是 .
A、2 B、 C、 D、42. 如图,四边形 中, , 平分 , , ,则 的长是 . 3. 综合与实践:
3. 综合与实践:“善思”小组开展“探究四点共圆的条件”活动,得出结论:对角互补的四边形四个顶点共圆.该小组继续利用上述结论进行探究.
提出问题:
如图1所示,在线段同侧有两点 , , 连接 , , , , 如果 , 那么 , , , 四点在同一个圆上.

探究展示:
如图2所示,作经过点 , , 的 , 在劣弧上取一点(不与 , 重合),连接 , ,

则 , (依据
,
,
点 , , , 四点在同一个圆上,(对角互补的四边形四个顶点共圆)
点 , 在点 , , 所确定的上,(依据
点 , , , 四点在同一个圆上;
反思归纳:
(1)上述探究过程中的“依据1”、“依据2”分别是指什么?
依据1:______;(从右边框内选一个选项,直接填序号)
依据2:______.(从右边框内选一个选项,直接填序号)
①圆内接四边形对角互补;
②对角互补的四边形四个顶点共圆;
③过不在同一直线上的三个点有且只有一个圆;
④经过两点的圆的圆心在这两点所连线段的垂直平分线上;
(2)如图3所示,在四边形中, , , 则的度数为______.
 4. 阅读下列材料,完成相应学习任务:
4. 阅读下列材料,完成相应学习任务:四点共圆的条件
我们知道,过任意一个三角形的三个顶点能作一个圆,过任意一个四边形的四个顶点能作一个圆吗?小明经过实践探究发现:过对角互补的四边形的四个顶点能作一个圆,下面是小明运用反证法证明上述命题的过程:
已知:在四边形ABCD中,∠B+∠D=180°.
求证:过点A、B、C、D可作一个圆.
证明:如图(1),假设过点A、B、C、D四点不能作一个圆,过A、B、C三点作圆,若点D在圆外,设AD与圆相交于点E,连接CE,则∠B+∠AEC=180° , 而已知∠B+∠D=180°,所以∠AEC=∠D,而∠AEC是△CED的外角,∠AEC>∠D,出现矛盾,故假设不成立,因此点D在过A、B、C三点的圆上.
如图(2)假设过点A、B、C、D四点不能作一个圆,过A、B、C三点作圆,若点D在圆内,设AD的延长线与圆相交于点E,连接CE,则∠B+∠AEC=180° , 而已知∠B+∠ADC=180°,所以∠AEC=∠ADC,而∠ADC是△CED的外角,∠ADC>∠AEC,出现矛盾,故假设不成立,因此点D在过A、B、C三点的圆上.
因此得到四点共圆的条件:过对角互补的四边形的四个顶点能作一个圆.
学习任务:
 (1)、材料中划线部分结论的依据是 .(2)、证明过程中主要体现了下列哪种数学思想: (填字母代号即可)A、函数思想 B、方程思想 C、数形结合思想 D、分类讨论思想(3)、如图(3),在四边形ABCD中,∠ABC=∠ADC=90°,∠CAD=16°.AD=BD,则求∠ADB的大小.
(1)、材料中划线部分结论的依据是 .(2)、证明过程中主要体现了下列哪种数学思想: (填字母代号即可)A、函数思想 B、方程思想 C、数形结合思想 D、分类讨论思想(3)、如图(3),在四边形ABCD中,∠ABC=∠ADC=90°,∠CAD=16°.AD=BD,则求∠ADB的大小.二、能力提升
-
5. 如图,RT中, , 以点为顶点在外部作 , 连接 , 若 , 则长为( )
 A、 B、 C、 D、6. 如图,点是正方形的边上一点,将绕着顶点逆时针旋转 , 得 , 连接 , 若为的中点,则下列结论正确的是( )
A、 B、 C、 D、6. 如图,点是正方形的边上一点,将绕着顶点逆时针旋转 , 得 , 连接 , 若为的中点,则下列结论正确的是( ) A、 B、 C、 D、7. 如图,正方形的边长为6,点E,F分别在线段 , 上,且 , , 若点M,N分别在线段 , 上运动,P为线段上的点,在运动过程中,始终保持 , 则线段的最小值为 .
A、 B、 C、 D、7. 如图,正方形的边长为6,点E,F分别在线段 , 上,且 , , 若点M,N分别在线段 , 上运动,P为线段上的点,在运动过程中,始终保持 , 则线段的最小值为 . 8. 如图,四边形ABCD中,∠BAD=∠BCD=90°,∠B=45°,DE⊥AC于E交AB于F,若BC=2CD,AE=2,则线段BF=。
8. 如图,四边形ABCD中,∠BAD=∠BCD=90°,∠B=45°,DE⊥AC于E交AB于F,若BC=2CD,AE=2,则线段BF=。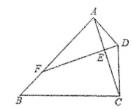 9. 已知:在△ABC中,AB=AC=6,∠B=30°,E为BC上一点,BE=2EC,DE=DC,∠ADC=60°。则AD的长为。
9. 已知:在△ABC中,AB=AC=6,∠B=30°,E为BC上一点,BE=2EC,DE=DC,∠ADC=60°。则AD的长为。 10. 如图1,中, , , 过点任作一条直线 , 将线段沿直线翻折得线段 , 直线交直线于点直线交直线于点 .
10. 如图1,中, , , 过点任作一条直线 , 将线段沿直线翻折得线段 , 直线交直线于点直线交直线于点 . (1)、小智同学通过思考推得当点在上方时,的角度是不变的,请按小智的思路帮助小智完成以下推理过程:
(1)、小智同学通过思考推得当点在上方时,的角度是不变的,请按小智的思路帮助小智完成以下推理过程:,
、、三点在以为圆心,以为半径的圆上.
填写数量关系
(2)、如图2,连接 , 求证:、、、四点共圆;(3)、线段最大值为;若取的中点 , 则线段的最小值为 .三、拓展创新
-
11. 如图,在矩形中, , 点E为边上一动点,点F为的中点,连接 , 点G在上,且 , 则下列结论:①在点E从点D运动到点A的过程中,点F运动的路径长为;②的最小值为16;③点G到的中点的距离为定值;④的最小值为 . 其中正确的是( )
 A、①②③ B、①②④ C、①③④ D、①②③④12. 如图,在正方形ABCD中,点H在AD边上(不与点A、D重合),∠BHF=90°,HF交正方形外角的平分线DF于点F , 连接AC交BH于点M , 连接BF交AC于点G , 交CD于点N , 连接BD . 则下列结论:
A、①②③ B、①②④ C、①③④ D、①②③④12. 如图,在正方形ABCD中,点H在AD边上(不与点A、D重合),∠BHF=90°,HF交正方形外角的平分线DF于点F , 连接AC交BH于点M , 连接BF交AC于点G , 交CD于点N , 连接BD . 则下列结论:①∠HBF=45°;②点G是BF的中点;③若点H是AD的中点,则sin∠NBC;④BNBM;⑤若AHHD , 则S△BNDS△AHM . 其中正确的结论是( )
 A、①②③④ B、①③⑤ C、①②④⑤ D、①②③④⑤13. 如图,在正方形ABCD中,M,N分别是AB,CD的中点,P是线段MN上的一点,BP的延长线交AD于点E,连接PD,PC,将△DEP绕点P顺时针旋转90°得△GFP,则下列结论:①CP=GP;②∠CGF=45°;③BC垂直平分FG;④若AB=4,点E在AD边上运动,则D,F两点之间距离的最小值是 . 其中结论正确的序号有( )
A、①②③④ B、①③⑤ C、①②④⑤ D、①②③④⑤13. 如图,在正方形ABCD中,M,N分别是AB,CD的中点,P是线段MN上的一点,BP的延长线交AD于点E,连接PD,PC,将△DEP绕点P顺时针旋转90°得△GFP,则下列结论:①CP=GP;②∠CGF=45°;③BC垂直平分FG;④若AB=4,点E在AD边上运动,则D,F两点之间距离的最小值是 . 其中结论正确的序号有( ) A、②③ B、①②③ C、①②④ D、①③④14. 在中, , , 为平面内的一点.
A、②③ B、①②③ C、①②④ D、①③④14. 在中, , , 为平面内的一点.图1
 图2
图2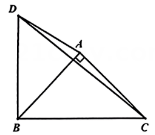 图3
图3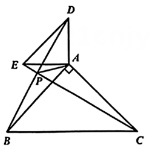 (1)、如图1,当点在边上时, , 且 , 求的长;(2)、如图2,当点在的外部,且满足 , 求证:;(3)、如图3, , 当、分别为、的中点时,把绕点顺时针旋转,设旋转角为 , 直线与的交点为 , 连接 , 直接写出旋转中面积的最大值.15. 综合与实践
(1)、如图1,当点在边上时, , 且 , 求的长;(2)、如图2,当点在的外部,且满足 , 求证:;(3)、如图3, , 当、分别为、的中点时,把绕点顺时针旋转,设旋转角为 , 直线与的交点为 , 连接 , 直接写出旋转中面积的最大值.15. 综合与实践“善思”小组开展“探究四点共圆的条件”活动,得出结论:对角互补的四边形四个顶点共圆.该小组继续利用上述结论进行探究.
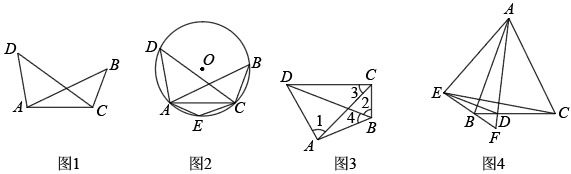
提出问题:
如图1,在线段AC同侧有两点B,D,连接 , 如果 , 那么A,B,C,D四点在同一个圆上.
探究展示:求证:点A,B,C,D四点在同一个圆上
如图2,作经过点A,C,D的 , 在劣弧上取一点E(不与A,C重合),连接 , , 则.
(1)、请完善探究展示(2)、如图3,在四边形中, , 则∠4的度数为.(3)、拓展探究:如图4,已知是等腰三角形, , 点D在上(不与的中点重合),连接.作点C关于的对称点E,连接并延长交的延长线于F,连接.①求证:A,D,B,E四点共圆;
②若 , 的值是否会发生变化,若不变化,求出其值;若变化,请说明理由
16. 已知是的角平分线, . (1)、观察猜想
(1)、观察猜想如图 , 当时,过点作交于点 , 连接 , 则的度数是 , 线段与的数量关系是 .
(2)、探究证明如图2,若 , 点是上任一点不与点 , 重合 , 过点作交于点 , 过点作交于点 , 连接 , 请写出的度数及线段与的数量关系,并就图2的情形说明理由.
(3)、解决问题在(2)的条件下,将绕点顺时针旋转得到 , 当点 , , 在同一直线上,时,请直接写出线段的长.