人教版数学九年级全册知识点训练营——二次函数的几何问题

试卷更新日期：2024-10-22 类型：复习试卷

进入 出卷网 下载

一、静态几何问题

  • 1. 如图，等腰直角三角形ABC中，∠A=90°，BC=8，点D、点E分别是BC、AC边上的点，DE//AB则S△BDE的最大值是（  ）

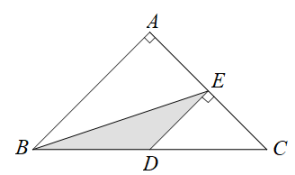    A、3 B、4 C、5 D、6

    查看试题解析

  • 2. 如图①，抛物线的顶点为M，平行于x轴的直线与该抛物线交于点A、B（点A在点B的左侧），根据对称性知△AMB恒为等腰三角形，我们规定：当△AMB为直角三角形时，就称△AMB为该抛物线的“完美三角形”。如图②，抛物线y=x2的“完美三角形”的斜边AB的长为

    查看试题解析

  • 3. 如图，顶点为M的抛物线y＝a（x+1）2﹣4分别与x轴相交于点A，B（点A在点B的右侧），与y轴相交于点C（0，﹣3）．

      

    (1)、求抛物线的函数表达式；
    (2)、判断△BCM是否为直角三角形，并说明理由．

    查看试题解析

二、动态几何问题

  • 4. 研究抛物线y=-12x2的性质时，将一个直角三角板的直角顶点置于平面直角坐标系的原点O，两直角边与该抛物线交于A，B两点（如图），将三角板绕点O旋转任意角度时发现，交点A，B所连线段总经过一个固定的点，则该定点的坐标是 ．

    查看试题解析

  • 5. 如图，抛物线y=12x2－8与x轴交于A、B两点，P是以点C（0，3）为圆心，2为半径的圆上的动点，Q是线段PA的中点，连结OQ.则线段OQ的最大值是.

    查看试题解析