人教版数学九年级全册知识点训练营——二次函数与一次函数

试卷更新日期：2024-10-22 类型：复习试卷

进入出卷网下载

一、夯实基础

1. 将二次函数 $y = - (x - k)^{2} + k + 1$ 的图象向右平移 $1$ 个单位，再向上平移 $2$ 个单位后，顶点在直线 $y = 2 x + 2$ 上，则 $k$ 的值为（）

A、 $2$ B、 $1$ C、 $0$ D、 $- 1$

查看试题解析
2. 一次函数y₁=mx+n(m≠0)与二次函数y₂=ax²+bx+c(a≠0)的图象如图所示，则不等式ax²+bx+c>mx+n的解集为（）

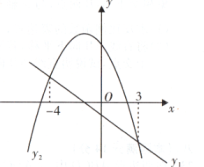A、-4<x<3 B、x<-4 C、3-<<x<-4 D、x>3或x<-4

查看试题解析
3. 如图，一次函数y=﹣x与二次函数为y=ax²+bx+c的图象相交于点M，N，则关于x的一元二次方程ax²+（b+1）x+c=0的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数 C、没有实数根 D、以上结论都正确

查看试题解析
4. 不论m取何实数，抛物线y=2（x+m）²+m的顶点一定在下列哪个函数图象上（　　）

A、y=2x² B、y=-x C、y=-2x D、y=x

查看试题解析
5. 如图，二次函数 $y_{1} = a x^{2} + b x + c (a \neq 0)$ 与一次函数 $y_{2} = m x + n (m \neq 0)$ 的图象相交于点 $A (- 1 ， 5)$ 和 $B (5 ， 2)$ ，则使不等式 $a x^{2} + b x + c < m x + n$ 成立的x的取值范围是.

查看试题解析
6. 抛物线y=x²+8x﹣4与直线x=﹣4的交点坐标是．

查看试题解析
7. 已知二次函数y＝x²＋bx＋c经过A(1，1)和B(－1，－3)，二次函数与一次函数y＝－x－2交于C ， D两点．

(1)、求二次函数的解析式．

(2)、求三角形BCD的面积．

(3)、结合图象直接写出不等式x²＋bx＋c＞－x－2的解集．

查看试题解析
8. 绿色生态农场生产并销售某种有机产品，每日最多生产130kg，假设生产出的产品能全部售出，每千克的销售价y₁（元）与产量x（kg）之间满足一次函数关系y₁＝﹣ $\frac{3}{5}$ x+168，生产成本y₂（元）与产量x（kg）之间的函数图象如图中折线ABC所示.

(1)、求生产成本y₂（元）与产量x（kg）之间的函数关系式；

(2)、求日利润为W（元）与产量x（kg）之间的函数关系式；

(3)、当产量为多少kg时，这种产品获得的日利润最大？最大日利润为多少元？

查看试题解析

二、能力提升

9. 二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 和正比例函数 $y = \frac{2}{3} x$ 的图象如图所示，则方程 $a x^{2} + (b - \frac{2}{3}) x + c = 0 (a \neq 0)$ 的两根之和（）

A、大于 $0$ B、等于 $0$ C、小于 $0$ D、不能确定

查看试题解析
10. 在平面直角坐标系中，抛物线y＝ax²+bx+c（a≠0）与x轴交于A、B两点，A（﹣3，0），B（1，0），与y轴交点C的纵坐标在﹣3～﹣2之间，根据图象判断以下结论：①abc²＞0；② $\frac{4}{3}$ ＜b＜2；③若 $a x_{1}^{2}$ ﹣bx₁＝ $a x_{2}^{2}$ ﹣bx₂且x₁≠x₂ ，则x₁+x₂＝﹣2；④直线y＝﹣ $\frac{5}{6}$ cx+c与抛物线y＝ax²+bx+c的一个交点（m ， n）（m≠0），则m＝ $\frac{1}{2}$ ．其中正确的结论是（）

A、①②④ B、①③④ C、①②③ D、①②③④

查看试题解析
11. 已知抛物线 $y = a x^{2} + b x (a \neq 0)$ 和直线 $y = k x - b (k \neq 0)$ 交于 $A (x_{1}, y_{1}), B (x_{2}, y_{2})$ 两点，其中 $x_{1} < 0 < x_{2}$ ，且满足 $| x_{1} | > | x_{2} |$ ，则直线 $y = a x + k$ 一定经过（）

A、第一、二象限 B、第二、三象限 C、第三、四象限 D、第一、四象限

查看试题解析
12. 已知 $B (3, 3) 、 C (0, 3)$ .抛物线 $y = x^{2} - 2 x + a + 2$ 与线段BC至少有一个交点，则 $a$ 的取值范围是（）

A、 $- 2 ⩽ a ⩽ 1$ B、 $- 2 ⩽ a ⩽ 2$ C、 $1 ⩽ a < 2$ D、 $- 2 ⩽ a < 1$

查看试题解析
13. 将二次函数 $y = x^{2} - 5 x - 6$ 在 $x$ 轴上方的图象沿 $x$ 轴翻折到 $x$ 轴下方，图象的其余部分不变，得到一个新图象．若直线 $y = 2 x$ $+ b$ 与这个新图象有3个公共点，则 $b$ 的值为（）

A、 $- \frac{73}{4}$ 或-12 B、 $- \frac{73}{4}$ 或2 C、-12或2 D、 $- \frac{69}{4}$ 或-12

查看试题解析
14. 当 $0 \leq x \leq 4$ 时，直线 $y = a$ 与抛物线 $y = x^{2} - 2 x - 2$ 有交点，则a的取值范围是.

查看试题解析
15. 如图，点A在二次函数y＝ax²(a＞0)第一象限的图象上，AB⊥x轴，AC⊥y轴，垂足分别为B、C，连接BC，交函数图象于点D，DE⊥y轴于点E，则 $\frac{D E}{B O}$ 的值为..

查看试题解析
16. 如图，抛物线 $y = x^{2} + m x$ 与直线 $y = - x + b$ 交于点A(2，0)和点 $B$ ．
（1）求 $m$ 和 $b$ 的值；
（2）求点 $B$ 的坐标，并结合图象写出不等式 $x^{2} + m x > - x + b$ 的解集；
（3）点 $M$ 是直线 $A B$ 上的一个动点，将点 $M$ 向左平移 $3$ 个单位长度得到点 $N$ ，若线段 $M N$ 与抛物线只有一个公共点，直接写出点 $M$ 的横坐标 $x_{M}$ 的取值范围．

查看试题解析

三、拓展创新

17. 已知直线 $y = - x - 3$ 与抛物线 $y = (x - m)^{2} - 4$ 对称轴左侧部分的图象有且只有一个交点，则m的取值范围是（）

A、 $m \leq \frac{5}{4}$ B、 $m \leq \frac{5}{4}$ 或 $m = \frac{7}{4}$ C、 $m \leq 1$ D、 $m \leq 1$ 或 $m = \frac{5}{4}$

查看试题解析
18. 如图，抛物线 $y = a x^{2} + b x + c$ （ $a \neq 0$ ）与x轴交于A ， B两点，与y轴交于点C ，其对称轴为直线 $x = 1$ ，直线 $y = x + c$ 与抛物线 $y = a x^{2} + b x + c$ （ $a \neq 0$ ）交于C ， D两点，且D为抛物线的顶点，则下列结论：① $C D = \sqrt{2}$ ；② $4 a + 2 b + c > 0$ ；③ $O A \cdot O B = - \frac{c}{a}$ ；④方程 $a x^{2} + b x = 1$ 有两个不相等的实数根．其中结论正确的个数有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
19. 函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象与x轴交于点(2，0)，顶点坐标为(-1，n)，其中 $n > 0$ ，以下结论正确的是（）
① $a b c > 0$ ；

②函数 $y = a x^{2} + b x + c (a \neq 0)$ 在 $x = 1 ， x = - 2$ 处的函数值相等；

③函数 $y = k x + 1$ 的图象与的函数 $y = a x^{2} + b x + c (a \neq 0)$ 图象总有两个不同的交点；

④函数 $y = a x^{2} + b x + c (a \neq 0)$ 在 $- 3 \leq x \leq 3$ 内既有最大值又有最小值．

A、①③ B、①②③ C、①④ D、②③④

查看试题解析
20. 抛物线 $y = a x^{2} + b x + c$ （ $a$ ， $b$ ， $c$ 是常数， $a < 0$ ）的顶点坐标为 $(1 ， m)$ ，其中 $m > 0$ ．下列四个结论：① $a b < 0$ ；② $c > 0$ ；③关于 $x$ 的一元二次方程 $a x^{2} + b x + c = m + 1$ 无实数解；④点 $P_{1} (n ， y_{1})$ ， $P_{2} (3 - 2 n ， y_{2})$ 在抛物线上，若 $n < 1$ ，则 $y_{1} < y_{2}$ ，能确定其正确的有（）个

A、1个 B、2个 C、3个 D、4个

查看试题解析
21. 已知函数 $y_{1} = k x + 4 k - 2$ （ $k$ 是常数， $k \neq 0$ ）， $y_{2} = a x^{2} + 4 a x - 5 a$ （ $a$ 是常数， $a \neq 0$ ），在同一平面直角坐标系中，若无论 $k$ 为何值，函数 $y_{1}$ 和 $y_{2}$ 的图象总有公共点，则 $a$ 的取值范围是．

查看试题解析
22. 若一个点的纵坐标是横坐标的2倍，则称这个点为“倍值点”，如： $A (1 ， 2)$ ， $B (- 2 ， - 4)$ ， $C (0 ， 0)$ 都是“倍值点”，若关于x的二次函数 $y = (m - 1) x^{2} + (m + 2) x + n (m$ ， n为常数， $m \neq 1)$ 总有两个不同的倍值点，则n的取值范围是．

查看试题解析
23. 如图，直线y= $\frac{1}{2}$ x+2与y轴交于点A，与直线y= $- \frac{1}{2}$ x交于点B．以AB为边向右作菱形ABCD，点C恰好与原点O重合．抛物线y=(x-h)²+k的顶点在直线y= $- \frac{1}{2}$ x上移动．若抛物线与菱形的边AB，BC都有公共点，则h的取值范围是

查看试题解析
24. 定义：在平面直角坐标系中，图形G上点P（x，y）的纵坐标y与其横坐标x的差y-x称为点P的“坐标差”，而图形G上所有点的“坐标差”中的最大值称为图形G的“特征值”
（1）点A（2，6）的“坐标差”为________；
（2）求抛物线y=-x²+5.x+4的“特征值”；
（3）某二次函数y=-x²+bx+c（c≠0）的“特征值”为-1，点B与点C分别是此二次函数的图象与x轴和y轴的交点，且点B与点C的“坐标差”相等，求此二次函数的解析式；
（4）二次函数y=-x²+px+q的图象的顶点在“坐标差”为2的一次函数的图象上，四边形DEFO是矩形，点E的坐标为（7，3），点O为坐标原点，点D在x轴上点下在x轴上，当二次函数y=-x²+px+q的图象与矩形的边只有三个交点时，求此二次函数的解析式及特征值.

查看试题解析