有理数的乘方运算—人教版数学七（上）知识点训练

试卷更新日期：2024-10-20 类型：复习试卷

进入出卷网下载

一、基础夯实

1. 下列各组数中，数值相等的是（）

A、 $3^{2}$ 和 $2^{3}$ B、 $(- 2)^{3}$ 和 $- 2^{3}$ C、 $- 3^{2}$ 和 $(- 3)^{2}$ D、 $- (- 2)$ 和 $- | - 2 |$

查看试题解析
2. 若 ${(a + 2)}^{2} + | b - 1 | = 0$ ，则 ${(a + b)}^{2024}$ 等于（）

A、 $- 2024$ B、 $- 1$ C、1 D、2024

查看试题解析
3. 13世纪数学家斐波那契的《计划书》中有这样一个问题：“在罗马有7位老妇人，每人赶着7头毛驴，每头驴驮着7只口袋，每只口袋里装着7个面包，每个面包附有7把餐刀，每把餐刀有7只刀鞘”，则刀鞘数为（）

A、42 B、49 C、 $7^{6}$ D、 $6^{7}$

查看试题解析
4. 计算： $- 2^{2} - {(- 2)}^{3} =$ .

查看试题解析
5. 若x、y互为倒数，则(-xy) ²⁰¹⁸=；

查看试题解析
6. 定义一种新运算：a＊b＝a²－b＋ab ．例如： $(- 1) * 3 = {(- 1)}^{2} - 3 + (- 1) \times 3 = - 5$ ，则4＊［2＊（－3）］＝．

查看试题解析
7. 计算下列各题：

(1)、 $- 2^{2} + 2 \times (- 3)^{2} + (- 6) \times (- 2)^{2}$

(2)、 $- 1^{4} - \frac{1}{6} \times [2 - (- 3)^{2}]$

(3)、 $(- 1)^{5} - [- 3 \times {(- \frac{2}{3})}^{2} - 1 \frac{1}{3} \div (- 2)^{2}]$

(4)、 $- 5^{2} \times | 1 - \frac{19}{15} | + \frac{3}{4} \times [{(- \frac{4}{3})}^{2} - 2^{3}]$

查看试题解析
8. 已知a，b互为相反数，c，d互为倒数，x的绝对值为 $5$ ．

(1)、a+b = ， cd = ， x = .

(2)、求 ${(a + b + c d)}^{2024} + {(- c d)}^{2023} - x$ 的值．

查看试题解析
9. 赵老师设计了接力游戏，用合作的方式完成有理数运算，规则如下：每人只能看到前一人给的式子，并进行一步计算，再将结果传递给下一人，最后完成运算过程如图所示：

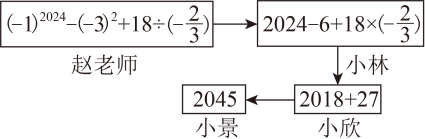(1)、接力中，计算错误的学生有．

(2)、请给出正确的计算过程．

查看试题解析

二、能力提升

10. 下列结论：①若 $a \neq b$ ，那么 $a^{2} \neq b^{2}$ ；②若 $| a | > | b |$ ，那么 $a > b$ ；③若 $a > | b |$ ，那么 $a^{2} > b^{2}$ ；④若 $a^{2} > b^{2}$ ，那么 $a > b$ ；⑤ $| a | + | b | = | a + b |$ ，则 $a b > 0$ ，其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
11. 计算(－2)⁹⁹＋(－2)¹⁰⁰的结果是（）

A、2⁹⁹ B、－2 C、2 D、－2⁹⁹

查看试题解析
12. $126 \times 3^{8} = p$ 若，则 $126 \times 3^{6}$ 的值可以表示为（）

A、 $\frac{1}{6} p$ B、 $p - 9$ C、 $p - 6$ D、 $\frac{1}{9} p$

查看试题解析
13. 一根1m长的绳子，第一次剪去绳子的 $\frac{1}{4}$ ，第二次剪去剩下绳子的 $\frac{1}{4}$ ，如此剪下去，第100次剪完后剩下绳子的长度是（　　）．

A、 ${(\frac{1}{4})}_{}^{100} m$ B、 ${(\frac{3}{4})}_{}^{100} m$ C、 ${(\frac{1}{4})}_{}^{99} m$ D、 ${(\frac{3}{4})}_{}^{99} m$

查看试题解析
14. 计算： $1 - 5 + 5^{2} - 5^{3} + 5^{4} - 5^{5} + \dots + 5^{2020} - 5^{2021} + 5^{2022} - \frac{5^{2023}}{6} =$ .

查看试题解析
15. 使用科学计算器进行计算，其按键顺序为：
则输出结果为．

查看试题解析
16. 计算

(1)、 $1 + 7 + 7^{2} + 7^{3} + \dots \dots + 7^{2022}$ 的值．

(2)、 $1 + 2 \times \frac{1}{3} + 3 \times {(\frac{1}{3})}^{2} + 4 \times {(\frac{1}{3})}^{3} + \dots + 9 \times {(\frac{1}{3})}^{8} + 10 \times {(\frac{1}{3})}^{9}$ ．

查看试题解析
17. 你能比较两个数 $2006^{2007}$ 和 $2007^{2006}$ 的大小吗？为了解决这个问题，先把问题一般化，比较 $n^{n + 1}$ 和 ${(n + 1)}^{n}$ 的大小（ $n \geq 1$ ，且n为正整数），然后从分析 $n = 1$ ， $n = 2$ ， $n = 3$ ， …这些简单情形入手，从中发现规律，经过归纳，猜想出结论．

(1)、通过计算，比较 $① - ⑦$ 各组中两个数的大小（在横线上填“<”“>”“=”）
① $1^{2}$ ______ $2^{1}$ ； ② $2^{3}$ ______ $3^{2}$ ； ③ $3^{4}$ ______ $4^{3}$ ； ④ $4^{5}$ ______ $5^{4}$ ；
⑤ $5^{6}$ ______ $6^{5}$ ； ⑥ $6^{7}$ ______ $7^{6}$ ； ⑦ $7^{8}$ ______ $8^{7}$ ．

(2)、从上面各小题目的结果经过归纳，可以猜想出 $n^{n + 1}$ 和 ${(n + 1)}^{n}$ 的大小关系是：
$n^{n + 1}$ ______ ${(n + 1)}^{n} (n \geq 3)$

(3)、由第二问可知： $2006^{2007}$ ______ $2007^{2006}$ ．

查看试题解析

三、拓展创新

18. 观察下列算式：
$3^{1} = 3$ ， $3^{2} = 9$ ， $3^{3} = 27$ ， $3^{4} = 81$ ， $3^{5} = 243$ ， $3^{6} = 729$ ， $3^{7} = 2187$ ， $3^{8} = 6561$ ， $\dots \cdot \cdot \cdot$ ，根据上述算式中的规律，你认为 $3^{2024}$ 的末位数字是（）

A、 $3$ B、 $9$ C、 $7$ D、 $1$

查看试题解析
19. 如图，每一幅图中均含有若干个正方形，第1幅图中有1个正方形；第2幅图中有5个正方形；…按这样的规律下去，第6幅图中有（　　）个正方形．

A、90 B、91 C、99 D、101

查看试题解析
20. 观察下面的式子的排列规律，写出它后面的式子：
$2 + \frac{2}{3} = 2^{2} \times \frac{2}{3}$ ， $3 + \frac{3}{8} = 3^{2} \times \frac{3}{8}$ ， $4 + \frac{4}{15} = 4^{2} \times \frac{4}{15}$ ，．

查看试题解析
21. $(1)$ 计算0.1² ， 1² ， 10² ， 100² ，观察这些结果，底数的小数点向左(或右)移动一位时，平方数的小数点有什么移动规律?
$(2)$ 计算0.1³ ， 1³ ， 10³ ， 100³ ，观察这些结果，底数的小数点向左(或右)移动一位时，立方数的小数点有什么移动规律?
$(3)$ 计算0.1⁴ ， 1⁴ ， 10⁴ ， 100⁴. 观察这些结果，底数的小数点向左(或右)移动一位时，四次方数的小数点有什么移动规律?

查看试题解析
22. 生活中常用的十进制是用 $0 ～ 9$ 这十个数字来表示数，满十进一，
例： $212 = 2 \times 1 0^{2} + 1 \times 1 0^{1} + 2$ ；
计算机常用二进制来表示字符代码，它是用0和1两个数来表示数，满二进一，
例：二进制数10010转化为十进制数： $1 \times 2^{4} + 0 \times 2^{3} + 0 \times 2^{2} + 1 \times 2^{1} + 0$
$= 16 + 2$
$= 18$ ；
其他进制也有类似的算法…

(1)、【发现】根据以上信息，将二进制数“10110”转化为十进制数是；

(2)、【迁移】按照上面的格式将八进制数“4372”转化为十进制数；

(3)、【应用】在我国远古时期，人们通过在绳子上打结来记录数量，即“结绳计数”，如图所示是远古时期一位母亲记录孩子出生后的天数，在从右向左依次排列的不同绳子上打结，满五进一，根据图示，求孩子已经出生的天数．

查看试题解析
23. 【概念学习】
规定：求若干个相同的有理数（均不等0）的除法运算叫做除方，如 $2 \div 2 \div 2$ ， $(- 3) \div (- 3) \div (- 3) \div (- 3)$ 等．类比有理数的乘方，我们把 $2 \div 2 \div 2$ 记作2^③ ，读作“2的圈3次方”， $(- 3) \div (- 3) \div (- 3) \div (- 3)$ 记作 $(- 3)$ ^④ ，读作“ $- 3$ 的圈4次方”．一般地，把 $a \div a \div a \div \dots \div a$ （ $n$ 个 $a$ ， $a \neq 0$ ）记作a^圈ⁿ ，读作“ $a$ 的圈 $n$ 次方”．
【初步探究】
（1）直接写出计算结果： $2^{⑤} =$ ________， ${(- \frac{1}{3})}^{③} =$ ________．
（2）关于除方，下列说法错误的是（）．
A．任何非零数的圈3次方都等于它的倒数
B．对于任何正整数 $n$ ， 1的圈n次方 $= 1$ ，
C． $3^{④} = 4^{③}$
D．负数的圈奇数次方结果是负数，负数的圈偶数次方结果是正数
【初步探究】
我们知道，有理数的减法运算可以转化为加法运算，除法运算可以转化为乘法运算，有理数的除方运算如何转化为乘法运算呢？
$2^{④} = 2 \div 2 \div 2 \div 2 = 2 \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} = {(\frac{1}{2})}^{2}$
（3）试一试：仿照上面的算式，将下列运算结果直接写成幂的形式， ${(- 3)}^{⑤} =$ ________； ${(- \frac{1}{2})}^{⑥} =$ ________．
（4）想一想：将一个非零有理数 $a$ 的圈 $n$ 次方写成幂的形式是________．
（5）算一算： $6^{2} \div {(- \frac{1}{2})}^{⑤} \times {(- \frac{1}{3})}^{③} - {(- \frac{1}{4})}^{④} \div (- 4^{2})$ ．

查看试题解析