数轴与绝对值结合—人教版数学七(上)知识点训练
试卷更新日期:2024-10-20 类型:复习试卷
一、基础夯实
-
1. 如图,数轴上的点表示的数分别是 . 如果 , 且 , 那么该数轴的原点的位置应该在( )
 A、点的左侧 B、点的右侧 C、点与点之间且靠近点 D、点与点之间且靠近点2. 已知 , 在数轴上的位置如图所示,则化简的结果是
A、点的左侧 B、点的右侧 C、点与点之间且靠近点 D、点与点之间且靠近点2. 已知 , 在数轴上的位置如图所示,则化简的结果是 A、 B、 C、 D、3. 已知 , , 在数轴上的位置如图所示,则( )
A、 B、 C、 D、3. 已知 , , 在数轴上的位置如图所示,则( ) A、 B、 C、 D、4. 已知a,b,c在数轴上的位置如图所示,则( )
A、 B、 C、 D、4. 已知a,b,c在数轴上的位置如图所示,则( ) A、0 B、 C、 D、5. 数轴是一个非常重要的数学工具,它使数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“数形结合”的基础.我们知道,|a|表示数a到原点的距离,这是绝对值的几何意义.比如:|x﹣2|的几何意义是数轴上表示数x的点与表示数2的点的距离,|x+1|的几何意义是数轴上表示数x的点与表示数﹣1的点的距离.当|x+1|+|x﹣2|取得最小值时,求x的整数和是( )A、﹣1 B、0 C、1 D、26. 有理数 在数轴上对应的点的位置如图所示,则下列各式正确的个数有( )
A、0 B、 C、 D、5. 数轴是一个非常重要的数学工具,它使数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“数形结合”的基础.我们知道,|a|表示数a到原点的距离,这是绝对值的几何意义.比如:|x﹣2|的几何意义是数轴上表示数x的点与表示数2的点的距离,|x+1|的几何意义是数轴上表示数x的点与表示数﹣1的点的距离.当|x+1|+|x﹣2|取得最小值时,求x的整数和是( )A、﹣1 B、0 C、1 D、26. 有理数 在数轴上对应的点的位置如图所示,则下列各式正确的个数有( )① ;② ;③ ;④ .
 A、1个 B、2个 C、3个 D、4个7. 观察有理数a , b , c在数轴上的位置,如图所示,
A、1个 B、2个 C、3个 D、4个7. 观察有理数a , b , c在数轴上的位置,如图所示,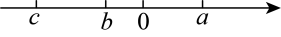 (1)、比较大小: 0, 0,0;(2)、化简: .
(1)、比较大小: 0, 0,0;(2)、化简: .二、能力提升
-
8. 如图,数轴上的A,B,C三点所表示的数分别为a,b,c,AB=BC.如果 , 那么该数轴的原点O的位置应该在( )
 A、点A的左边 B、点B与点C之间 C、点A与点B之间 D、点C的右边9. 实数 在数轴上的对应点的位置如图所示,若 ,则A,B,C,D四个点中可能是原点的为( )
A、点A的左边 B、点B与点C之间 C、点A与点B之间 D、点C的右边9. 实数 在数轴上的对应点的位置如图所示,若 ,则A,B,C,D四个点中可能是原点的为( ) A、A点 B、B点 C、C点 D、D点10. 数轴上的A,B,C三点所表示的数分别为a、b、1,且|a﹣1|+|b﹣1|=|a﹣b|,则下列选项中,满足A,B,C三点位置关系的数轴为( )A、
A、A点 B、B点 C、C点 D、D点10. 数轴上的A,B,C三点所表示的数分别为a、b、1,且|a﹣1|+|b﹣1|=|a﹣b|,则下列选项中,满足A,B,C三点位置关系的数轴为( )A、 B、
B、 C、
C、 D、
D、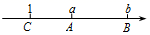 11. 点、在数轴上对应的数分别为 , , 满足 , 点在数轴上对应的数为 , 当时, .12. 有理数a、b、c在数轴上的位置如图所示,化简: .
11. 点、在数轴上对应的数分别为 , , 满足 , 点在数轴上对应的数为 , 当时, .12. 有理数a、b、c在数轴上的位置如图所示,化简: . 13. 若 互为相反数, 互为倒数,数轴上表示数 的点到 的距离是3,则 的值为.14. 有理数a,b,c在数轴上所表示的点的位置如图所示,则化简|a+b|-|c-b|+|c|-|c-a|= .
13. 若 互为相反数, 互为倒数,数轴上表示数 的点到 的距离是3,则 的值为.14. 有理数a,b,c在数轴上所表示的点的位置如图所示,则化简|a+b|-|c-b|+|c|-|c-a|= . 15. 阅读材料
15. 阅读材料
材料:学习绝对值时,我们知道表示数的点与原点的距离,即 , 也可以说表示数轴上数与数对应的两点之间的距离,同理,数轴上数和数两点间的距离可以表示为或 .
例如数轴上表示和的两点间的距离为或 .
发现解题规律:
若 , 则或;
若 , 则或 , 得或;
若 , 则或 , 得或 .
结合上面的发现解决下列问题.(1)、数轴上表示和两点之间的距离是 .(2)、若 , 则 或 .(3)、如图所示,当点、所表示的数分别为和时,是否存在一点 , 使得点到、两点的距离之和等于?若存在,设点表示的数为 , 求的值;若不存在,请说明理由.
三、拓展创新
-
16. 点A、B在数轴上所对应的数分别是x、y,其中x、y满足(x﹣3)2+|y+5|=0.若点D是AB的中点,O为原点,数轴上有一动点P,|PD|、|PO|分别表示数轴上P与D,P与O两点间的距离,则|PD|﹣|PO|的最小值是 .17. 已知,数轴上A,B,C三点对应的有理数分别为a,b,c.其中点A在点B左侧,A,B两点间的距离为2,且a,b,c满足 , 则a= . 对数轴上任意一点P,点P对应数x,若存在x使的值最小,则x的值为 .18. 如图在数轴上A点表示数a , B点表示数b , a、b满足;
 (1)、点A表示的数为 ▲ ;点B表示的数为 ▲ ;(2)、若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),
(1)、点A表示的数为 ▲ ;点B表示的数为 ▲ ;(2)、若在原点O处放一挡板,一小球甲从点A处以1个单位/秒的速度向左运动;同时另一小球乙从点B处以2个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反的方向运动,设运动的时间为t(秒),①当时,甲小球到原点的距离 ▲ ;乙小球到原点的距离 ▲ _;
当时,甲小球到原点的距离 ▲ ;乙小球到原点的距离 ▲ ;
②试探究:甲,乙两小球到原点的距离可能相等吗?若不能,请说明理由,若能,请直接写出甲,乙两小球到原点的距离相等时经历的时间.