绝对值的非负性—人教版数学七(上)知识点训练
试卷更新日期:2024-10-20 类型:复习试卷
一、基础夯实
-
1. 下列说法正确的是( )A、一个有理数的绝对值不小于它自身 B、若两个有理数的绝对值相等,则这两个数相等 C、若两个有理数的绝对值相等,则这两个数互为相反数 D、 的绝对值等于2. 下列说法正确的是( )A、|x|<x B、若|x-1|+2取最小值,则x=0 C、若x>1>y>-1,则|x|<|y| D、若|x+1|≤0,则x=-13. 若(m﹣2)2+|n+3|=0,则﹣(2m+n)2024的值是( )A、﹣1 B、1 C、2024 D、﹣20244. 表示x、y两数的点在数轴上的位置如图所示,则等于( )
 A、 B、 C、 D、5. |a﹣2|+|b+1|=0,则a+b等于( )A、﹣1 B、1 C、0 D、﹣26. 已知|a+b+2|+|b﹣3|=0,则a﹣2b的值是( )A、﹣5 B、11 C、5 D、﹣117. 若|m﹣n|=n﹣m , 且|m|=4,|n|=3,则m+n=( )A、1或﹣1 B、﹣1或7 C、1或﹣7 D、﹣1或﹣78. 若与互为相反数,则( )A、5 B、 C、1 D、9. 若 , 互为相反数,则; .10. 已知b、c满足 , 则的值是 .11. 已知那么 .12. 已知 , 求的值.13. 先化简,再求值: , 其中x , y满足等式 .14. 已知、、为的三边长,且、满足 , 为方程的解,求的周长.
A、 B、 C、 D、5. |a﹣2|+|b+1|=0,则a+b等于( )A、﹣1 B、1 C、0 D、﹣26. 已知|a+b+2|+|b﹣3|=0,则a﹣2b的值是( )A、﹣5 B、11 C、5 D、﹣117. 若|m﹣n|=n﹣m , 且|m|=4,|n|=3,则m+n=( )A、1或﹣1 B、﹣1或7 C、1或﹣7 D、﹣1或﹣78. 若与互为相反数,则( )A、5 B、 C、1 D、9. 若 , 互为相反数,则; .10. 已知b、c满足 , 则的值是 .11. 已知那么 .12. 已知 , 求的值.13. 先化简,再求值: , 其中x , y满足等式 .14. 已知、、为的三边长,且、满足 , 为方程的解,求的周长.二、能力提升
-
15. 已知a,b都是有理数,如果|a+b|=b-a,那么对于下列两种说法:①a可能是负数;②b一定不是负数.其中判断正确的是( )A、①②都错 B、①②都对 C、①错②对 D、①对②错16. 已知0≤a≤4,那么|a﹣2|+|3﹣a|的最大值等于( )A、1 B、5 C、8 D、317. 若a=-2020,则式子 的值是( )A、4036 B、4038 C、4040 D、404218. 式子|x﹣3|+|x+4|有最小值,其最小值是 .19. 小宇是七年级(1)班数学学习小组长,他想带领本小组同学一起复习绝对值的相关知识,整理了以下题目:
 (1)、|﹣5|=;(2)、若|x|=4,则x的值为 ;(3)、若|a﹣3|与|2b﹣4|互为相反数,则a﹣b=;(4)、若|x+3|+|x﹣2|=5,则所有符合条件的整数x的和为 ;(5)、有理数a、b、c在数轴上的位置如图所示,化简|a+b|+|a﹣c|+|b﹣c|的结果是 ;(6)、若你是学习小组成员,请针对绝对值的复习给大家提一条复习建议.
(1)、|﹣5|=;(2)、若|x|=4,则x的值为 ;(3)、若|a﹣3|与|2b﹣4|互为相反数,则a﹣b=;(4)、若|x+3|+|x﹣2|=5,则所有符合条件的整数x的和为 ;(5)、有理数a、b、c在数轴上的位置如图所示,化简|a+b|+|a﹣c|+|b﹣c|的结果是 ;(6)、若你是学习小组成员,请针对绝对值的复习给大家提一条复习建议.三、拓展创新
-
20. 已知线段 , 点C是直线AB上一点,点D为线段AC的中点, , 且m、n满足 , 则线段BD的长为 .21. 规定: , , 例如 , , 下列结论中,正确的是(填写序号)
①若 , 则; ②若 , 则;
③能使成立的x的值不存在;④式子的最小值是5.
22. 综合探究阅读材料:数轴是学习有理数的一种重要工具,任何有理数都可以用数轴上的点表示,这样能够运用数形结合的方法解决一些问题.例如,两个有理数在数轴上对应的点之间的距离可以用这两个数的差的绝对值表示;
在数轴上,有理数与对应的两点之间的距离为;
在数轴上,有理数与对应的两点之间的距离为;
在数轴上,有理数与对应的两点之间的距离为;
在数轴上,有理数与对应的两点之间的距离为;
如图 , 在数轴上有理数对应的点为点 , 有理数对应的点为点 , , 两点之间的距离表示为或 , 记为 .
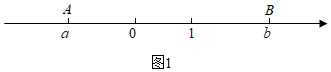 (1)、解决问题:数轴上有理数与对应的两点之间的距离等于;数轴上有理数与对应的两点之间的距离用含的式子表示为;若数轴上有理数与对应的两点 , 之间的距离 , 则等于;(2)、联系拓广如图 , 点 , , 是数轴上的三点,点表示的数为 , 点表示的数为 , 动点表示的数为 .
(1)、解决问题:数轴上有理数与对应的两点之间的距离等于;数轴上有理数与对应的两点之间的距离用含的式子表示为;若数轴上有理数与对应的两点 , 之间的距离 , 则等于;(2)、联系拓广如图 , 点 , , 是数轴上的三点,点表示的数为 , 点表示的数为 , 动点表示的数为 .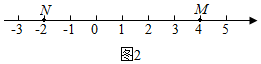
若点在点 , 之间,则 .
若 , 即点到点的距离等于点到点距离的倍,则等于 .
能力提升:若点在点 , 之间,则 .
若 , 则等于 .