绝对值的化简—人教版数学七（上）知识点训练

试卷更新日期：2024-10-20 类型：复习试卷

进入出卷网下载

一、基础夯实

1. 有理数 $a$ ， $b$ ， $c$ 在数轴上的位置如图，则 $| a + c | + | c - b | - | b - a | =$ （）

A、 $- 2 b$ B、 $0$ C、 $2 c$ D、 $2 c - 2 b$

查看试题解析
2. 若 $2 < a < 4$ ，则 $| 2 - a | + | 4 - a |$ 等于（）

A、 $- 2$ B、 $2$ C、 $2 a - 6$ D、 $6 - 2 a$

查看试题解析
3. 计算 $| - 2024 |$ 的结果是（）

A、 $2024$ B、 $\frac{1}{2024}$ C、 $- 2024$ D、 $- \frac{1}{2024}$

查看试题解析
4. 数轴上表示有理数a的点如图所示，则化简代数式 $| a | + | 1 + a |$ 的结果是（　　）

A、 $2 a + 1$ B、 $- 2 a - 1$ C、1 D、 $- 1$

查看试题解析
5. $- | - 3 |$ 的相反数是（）

A、 $- 3$ B、3 C、 $\frac{1}{3}$ D、 $- \frac{1}{3}$

查看试题解析
6. 下列有理数大小关系判断正硧的是（）

A、 $- (- \frac{1}{9}) > - |- \frac{1}{10}|$ B、 $0 > |- 10|$ C、 $|- 3| < |+ 3|$ D、 $- 1 > - 0.01$

查看试题解析
7. 如果|a|=| $-$ 2|，那么a=；如果m是负数，且 $| m | = 10,$ 那么m= .

查看试题解析
8. 若： $3 < a < 10,$ 那么 $| 3 - a | + | a - 10 | =$ .

查看试题解析
9. 若有理数 $a 、 b 、 c$ 在数轴上对应的点如图，化简： $| a - c | + | b + c | - | a - b | =$ ．

查看试题解析
10. 看图，回答下列问题：

(1)、用"＞"或"＜"填空：
b－c0，a＋b0，c－a0；

(2)、化简：|b－c|＋2|a＋b|－|c－a|.

查看试题解析

二、能力提升

11. 实数a ， b ， c在数轴上对应点的位置如图所示．以下结论正确的是（　　）

A、 $a c < 0$ B、 $| a + b | = - a - b$ C、 $| c - a | = a - c$ D、 $| a | > | b |$

查看试题解析
12. 若 $a b < 0$ ，则 $\frac{| a |}{a} + \frac{b}{| b |} =$ （）

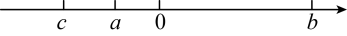A、 $- 2$ B、0 C、2 D、 $- 2$ 或2或0

查看试题解析
13. 已知有理数a、b、c满足 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c} = 1$ ，则 $\frac{a b c}{| a b c |} =$ （）

A、3 B、 $- 3$ C、1 D、 $- 1$

查看试题解析
14. 代数式 $\frac{a}{|a|} + \frac{b}{|b|} + \frac{a b}{|a b|}$ 的所有可能的值有．

查看试题解析
15. 已知 $a ， b ， c$ 为有理数，且 $a + b - c = 0 ， a b c < 0$ ，则 $\frac{b - c}{| a |} + \frac{a - c}{| b |} + \frac{a + b}{| c |}$ 的值为．

查看试题解析
16. 学习了绝对值的概念后，我们可以认为：一个非负数的绝对值等于它本身，负数的绝对值等于它的相反数，即当a＜0时，|a|＝﹣a ，根据以上阅读完成下面的问题：

(1)、 $| 3.14 - π | =$ ；

(2)、如果有理数 $a < b$ ，则 $| a - b | =$ ；

(3)、请利用你探究的结论计算下面式子：
$| \frac{1}{2} - 1 | + | \frac{1}{3} - \frac{1}{2} | + | \frac{1}{4} - \frac{1}{3} | + ⋯ + | \frac{1}{2022} - \frac{1}{2021} | + | \frac{1}{2023} - \frac{1}{2022} |$

(4)、如图，数轴上有a、b、c三点，化简 $| a | + | a + b | - 2 | b - c |$ .

查看试题解析
17. 在解决数学问题的过程中，我们常用到“分类讨论”的数学思想，下面是运用分类讨论思想解决问题的过程，请仔细阅读，并解答问题．
⑴[提出问题]三个有理数a，b，c满足abc＞0，求 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 的值．
⑵[解决问题]由题意，得a，b，c三个有理数都为正数或其中一个为正数，另外两个为负数．
①a，b，c都是正数，即a＞0，b＞0，c＞0时，则 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ = $\frac{a}{a} + \frac{b}{b} + \frac{c}{c}$ ＝1+1+1＝3；
②当a，b，c中有一个为正数，另外两个为负数时，不妨设a＞0，b＜0，c＜0，则 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ ＝ $\frac{- a}{a} + \frac{- b}{b} + \frac{- c}{c}$ ＝1+（-1）+（-1）＝-1．
综上所述， $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 的值为3或-1．
⑶[探究拓展]请根据上面的解题思路解答下面的问题：

(1)、已知a，b是不为0的有理数，当|ab|＝-ab时，则 $\frac{| a |}{a} + \frac{| b |}{b}$ 的值是；

(2)、已知a，b，c是有理数，当abc＜0时，求 $\frac{| a |}{a} + \frac{| b |}{b} + \frac{| c |}{c}$ 的值；

(3)、已知a，b，c是有理数，a+b+c＝0，abc＜0，求 $\frac{b + c}{| a |} + \frac{c + a}{| b |} + \frac{a + b}{| c |}$ 的值．

查看试题解析

三、拓展创新

18. 在多项式 $x - y - z - m - n$ （其中 $x > y > z > m > n$ ）中，对相邻的两个字母间任意添加绝对值符号，添加绝对值符号后仍只有减法运算，然后进行去绝对值运算，称此为“绝对操作”．例如： $x - y - | z - m | - n = x - y - z + m - n ， | x - y | - z - | m - n | = x - y - z - m + n ， \cdot \cdot \cdot$ ．下列说法：
①存在“绝对操作”，使其运算结果与原多项式相等；②不存在“绝对操作”，使其运算结果与原多项式之和为0；③所有的“绝对操作”共有5种不同运算结果．
其中正确的个数是（）

A、0 B、1 C、2 D、3

查看试题解析
19. 如果对于某一特定范围内的任意允许值，P = |1 - 4x| + |1 - 5 x |+|1-6 x| + |1 - 7 x| + |1 - 8 x |的值恒为一常数，则此值为.

查看试题解析
20. 阅读下列材料：我们知道
$\begin{matrix} |x| \end{matrix} = \{\begin{array}{l} x (x > 0) \\ 0 (x = 0) \\ - x (x < 0) \end{array}$
现在我们可以用这个结论来化简含有绝对值的代数式，如化简代数式 $|x + 1| + |x - 2|$ 时，令 $x + 1 = 0$ ，求得 $x = - 1$ ；令 $x - 2 = 0$ ，求得 $x = 2$ （称-1，2分别为 $| x + 1 |$ ， $| x - 2 |$ 的零点值）.在有理数范围内，零点值-1和2可将全体有理数分成不重复且不遗漏的如下3种情况：
①当 $x < - 1$ 时，原式 $= - (x + 1) - (x - 2) = - 2 x + 1$ ；
②当 $- 1 \leq x \leq 2$ 时，原式 $= x + 1 - (x - 2) = 3$ ；
③当 $x > 2$ 时，原式 $= x + 1 + x - 2 = 2 x - 1$ .
综上所述，
$|x + 1| + |x - 2| = \{\begin{array}{l} - 2 x + 1 (x < - 1) \\ 3 (- 1 \leq x \leq 2) \\ 2 x - 1 (x > 2) \end{array}$
通过以上阅读，请你解决以下问：
(1)分别求出 $| x + 2 |$ 和 $| x - 4 |$ 的零点值；
(2)化简代数式 $| x + 2 | + | x - 4 |$ .

查看试题解析