浙教版数学七上考点突破训练：化简多重符号、绝对值的化简、绝对值非负性应用

试卷更新日期：2024-10-20 类型：复习试卷

进入出卷网下载

一、化简多重符号

1. 下列说法错误的是（）

A、 $+ (- 2)$ 的相反数是 $2$ B、 $- (+ 4)$ 的相反数是 $4$ C、 $- (- 6)$ 的相反数是 $- 6$ D、 $- (+ \frac{1}{3})$ 的相反数是 $3$

查看试题解析
2. 下列各数中，互为相反数的是（）

A、 $- (- 3)$ 和 $|- 3|$ B、 $- 2$ 和 $- (- 2)$ C、 $- |- \frac{1}{2}|$ 和 $- (+ \frac{1}{2})$ D、 $0.6$ 和 $- (- |- 0.6|)$

查看试题解析
3. 在﹣（﹣2），﹣|﹣7|，﹣|+1|，|﹣ $\frac{2}{3}$ |，﹣（+0.8）中负数的个数是（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 下列比较大小，正确的是（　　）

A、-5＜-7 B、-（-3）＜|3| C、 $- \frac{1}{2} > - \frac{1}{3}$ D、 $| - \frac{1}{6} | > - \frac{1}{7}$

查看试题解析
5. 化简 $- [- (- 3 \frac{3}{7})]$ ．

查看试题解析
6. 在 $- (- \frac{1}{2}) ， - 1 ， | 3 - π | ， 0$ 这四个数中，最小的数是.

查看试题解析
7. 化简

(1)、 $- (- 68)$ ；

(2)、 $- (+ 0.75)$ ；

(3)、 $- (- \frac{3}{5})$ ；

(4)、 $- [+ (- 3.6)]$

查看试题解析
8. （1）化简下列各式：
① $- (- 5) =$ ___________；
② $- (+ 5) =$ __________；
③ $- [- (- 5)] =$ ___________；
④ $- [- (+ 5)] =$ __________；
⑤ $- \{- [- (- 5)]\} =$ ______________；
⑥ $- \{- [- (+ 5)]\} =$ ____________
（2）根据你所发现的规律，猜想当 $- 5$ 前面有2022个负号时，化简后结果是多少?当 $+ 5$ 前面有2022个负号时，化简后结果是多少?
（3）结合（2）中的规律，用文字叙述你所得到的结论.

查看试题解析

二、绝对值的化简

9. 有理数a、b在数轴上的位置如图所示，则 $| a - b | + | b - a |$ 化简后为（）

A、 $2 a - 2 b$ B、 $2 b - 2 a$ C、0 D、 $- 2 b$

查看试题解析
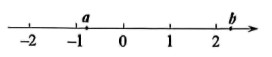10. 已知 $a$ 、 $b$ 、 $c$ 都为整数，且满足 $| a - b |^{2023} + | b - c |^{2024} = 1$ ，则 $| a - b | + | b - c | - | a - c |$ 的结果为（）

A、0 B、0或1 C、1 D、1或2

查看试题解析
11. 若m ， n是有理数，满足 $| m | < | n |$ ，且 $m > 0$ ， $n < 0$ ，则下列选项中正确的是（）

A、 $- m < n < - n < m$ B、 $n < - m < m < - n$ C、 $- n < - m < n < m$ D、 $- m < - n < n < m$

查看试题解析
12. 在多项式 $x - y - z - m - n$ （其中 $x > y > z > m > n$ ）中，对相邻的两个字母间任意添加绝对值符号，添加绝对值符号后仍只有减法运算，然后进行去绝对值运算，称此为“绝对操作”．例如 $x - y - | z - m | - n = x - y - z + m - n$ ， $| x - y | - z - | m - n | = x - y - z - m + n$ ， ……则所有“绝对操作”共有（）种不同运算结果

A、7 B、6 C、5 D、4

查看试题解析
13. 有理数 $a$ 、 $b$ 、 $c$ 在数轴上的位置如图：

(1)、比较大小（填“ $>$ ”或“ $<$ ”号）．① $a$ $c$ ；② $a + b$ $0$ ；③ $b - c$ $0$ ；

(2)、化简： $| b - c | + 2 | a + b | - | c - a |$ ．

查看试题解析
14. 已知A ， $B$ ， $C$ 三点在数轴上的位置如图所示，它们表示的数分别是 $a$ ， $b$ ， $c$ ．

(1)、填空： $a$ 0， $b$ 0， $c$ 0， $a + c$ 0（填“ $>$ ”“ $<$ ”或“ $=$ ”）；

(2)、化简： $| a - b | - 2 | a + c | + | b - c |$ ．

查看试题解析
15. 学习了绝对值的概念后，我们可以认为：一个非负数的绝对值等于它本身，负数的绝对值等于它的相反数，即当a＜0时，|a|＝﹣a ，根据以上阅读完成下面的问题：

(1)、 $| 3.14 - π | =$ ；

(2)、如果有理数 $a < b$ ，则 $| a - b | =$ ；

(3)、请利用你探究的结论计算下面式子：
$| \frac{1}{2} - 1 | + | \frac{1}{3} - \frac{1}{2} | + | \frac{1}{4} - \frac{1}{3} | + ⋯ + | \frac{1}{2022} - \frac{1}{2021} | + | \frac{1}{2023} - \frac{1}{2022} |$

(4)、如图，数轴上有a、b、c三点，化简 $| a | + | a + b | - 2 | b - c |$ .

查看试题解析

三、绝对值非负性应用

16. 若 $| a - 1 | = 1 - a$ ，则a的取值范围是（）

A、 $a < 1$ B、 $a > 1$ C、 $a \leq 1$ D、 $a \geq 1$

查看试题解析
17. 满足 $| a b | + | a - b | - 1 = 0$ 的整数对（a，b）共有（）

A、4个 B、5个 C、6个 D、7个

查看试题解析
18. 如果a表示实数，那么|a|﹣a的值（）

A、不可能是负数 B、可能是零或者负数 C、必定是零 D、必定是正数

查看试题解析
19. 若 $| a - 2 |$ 与 $| m + n + 3 |$ 互为相反数，则 $a + m + n =$ （）

A、5 B、 $- 5$ C、1 D、 $- 1$

查看试题解析
20. 已知a，b都是有理数，如果|a+b|=b-a，那么对于下列两种说法：①a可能是负数；②b一定不是负数．其中判断正确的是（）

A、①②都错 B、①②都对 C、①错②对 D、①对②错

查看试题解析
21. 已知b、c满足 $| b - 1 | + | c - \frac{1}{2} | = 0$ ，则 $b + c$ 的值是．

查看试题解析
22. 已知线段 $A B = 10$ ，点C是直线AB上一点，点D为线段AC的中点， $\frac{B C}{A C} = \frac{m}{n}$ ，且m、n满足 $| m - 3 | + 5 {(m + 2 n - 7)}^{2} = 0$ ，则线段BD的长为．

查看试题解析
23. 规定： $f (x) = | x - 2 |$ ， $g (y) = | y + 1 |$ ，例如 $f (- 4) = | - 4 - 2 | = 6$ ， $g (- 4) = | - 4 + 1 | = 3$ ，下列结论中，正确的是（填写序号）
①若 $f (x) + g (y) = 0$ ，则 $y^{x} = - 1$ ； ②若 $- 1 < x < 2$ ，则 $f (x) - g (x) = - 2 x + 1$ ；
③能使 $f (x) = g (x)$ 成立的x的值不存在；④式子 $f (x - 1) + g (x + 1)$ 的最小值是5．

查看试题解析
24. 学习了绝对值的概念后，我们知道一个非负数的绝对值等于它本身，负数的绝对值等于它的相反数，即当 $a \geq 0$ 时， $| a | = a$ ；当 $a < 0$ 时， $| a | = - a$ .请完成下面的问题：

(1)、因为 $3 < π$ ，所以 $3 - π < 0$ ， $| 3 - π | =$ $- (3 - π)$ =；

(2)、若有理数 $a < b$ ，则 $| a - b | =$ ；

(3)、计算： $| \frac{1}{3} - \frac{1}{2} | + | \frac{1}{4} - \frac{1}{3} | + | \frac{1}{5} - \frac{1}{4} | + ⋯ + | \frac{1}{2022} - \frac{1}{2021} | + | \frac{1}{2023} - \frac{1}{2022} |$

查看试题解析
25. 任意一个正整数n都可以写成两个正整数x，y相乘的形式，我们把两个乘数的差的绝对值最小的一种分解称为该正整数的最优分解，并定义一种新运算“F(n)=|x-y|”，例：12=1×12=2×6=3×4，则F(12)=|3-4|=1.

(1)、填空：F(6)= ， F(18)=.

(2)、若F(n)=0(10<n<50)，求n的值.

查看试题解析