精选实践探究题—2024年浙教版数学七(上)期中复习
试卷更新日期:2024-10-19 类型:复习试卷
一、有理数
-
1. 符号“f”表示一种运算,它对一组数的运算如下:
, , , …
(1)、利用以上运算的规律写出;(为正整数)(2)、计算;(3)、计算的值.2. 根据以下素材,探索完成任务.素材1:如何规划游玩路线?
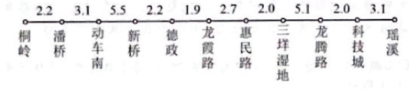
温州轨道交通实行里程分段计价票制,起步价2元,可乘坐4km(含4km),4至28km(含28km)每1元可乘4km(不足4km按1元算).如:桐岭站到动车南站共5.3km,收费3元.部分站点距离见下图(单位:km)

素材2:一名成年乘客可免费携带一名身高不足1.2米(含1.2米)的儿童乘车,
素材3:小明一家四口将乘坐轻轨出游.小明家住在新桥站附近,家庭成员如下:小明(身高1.5米)、弟弟(身高1.1米)、爸爸、妈妈.
问题解决
(1)、任务1从新桥站到桐岭站为km,单人单程乘坐需车费元
(2)、任务2小明一家乘坐轻轨从新桥站到三烊湿地站,需要多少车费.
(3)、任务3小明一家从新桥站出发,计划共用30元车费出行(往返),请你为小明一家规划一个尽可能远的游玩站点,并说明理由.
3. 素材1:每年秋天是灵昆柿子饼盛产期.小黄同学打算从灵昆寄5袋柿子饼到杭州,以每袋3千克为标准,超过的千克数记为正数,不足的千克数记为负数,记录如下表所示:柿子饼袋
①
②
③
④
⑤
与标准重量的差值(单位:千克)
0.1
-0.3
0
-0.1
0.2
素材2:小黄同学选择了某快递,收费标准如下:3千克以内15元(含3千克),超过1千克的部分为2元/每千克(不足1千克按1千克计).现该快递公司提供多种寄件方式:
纸箱类型
中型纸箱
大型纸箱
可容纳袋数(袋/个)
2
4
重量(千克/个)
0.4
0.7
价格(元/个)
3
5
方案一:小黄购买了中型纸箱将重量最低的②、④柿子饼袋打包在一起,其余每小袋各自寄出.
方案二:____.
(1)、【任务1】求这5袋柿子饼的总重量.(2)、【任务2】求方案一所需要的费用.(3)、【任务3】请你设计方案二,使它的费用低于方案一,并计算你的方案费用.4. 根据以下素材,探索完成任务.如何规划游玩路线?
素材1
温州轨道交通实行里程分段计价票制,起步价2元,可乘坐4km (含4km),4至28km(含28km)每1元可乘4km(不足4km按1元算).如:桐岭站到动车南站共5.3km,收费3元.部分站点距离见下图(单位:km)
素材2
一名成年乘客可免费携带一名身高不足1.2米(含1.2米)的儿童乘车,
素材3
小明一家四口将乘坐轻轨出游.小明家住在新桥站附近,家庭成员如下:小明(身高1.5米)、弟弟(身高1.1米)、爸爸、妈妈.
问题解决
(1)、任务1从新桥站到桐岭站为km,单人单程乘坐需车费元
(2)、任务2小明一家乘坐轻轨从新桥站到三烊湿地站,需要多少车费.
(3)、任务3小明一家从新桥站出发,计划共用30元车费出行(往返),请你为小明一家规划一个尽可能远的游玩站点,并说明理由.
5. 根据以下素材,尝试解决问题.如何获得更高的销售额?
素材
甲菜农有筐蔬菜,每筐质量在千克左右,超过的千克数记为正数,不足的千克数记为负数,记录如图,超过千克的以元筐的价格售出,其余三筐以元千克销售,全部售出.

素材
乙菜农将蔬菜堆放在一起进行销售,售出的蔬菜质量比甲菜农少千克,其中千克以元千克销售,剩下的部分按八折全部售出.
问题解决
(1)、问题1:求甲菜农售出最重的一筐蔬菜的质量.(2)、问题2:求乙菜农售出的蔬菜的总质量.(3)、问题3:甲、乙菜农的蔬菜全部售出后,比较哪一位菜农的销售额更高,高多少元?6. 国庆期间,某超市各个区域都有促销活动,晓琳一家去逛该超市,准备购买纸巾,根据以下素材,探索完成任务.揭秘超市促销:送券和打折哪个更优惠
素材1
纸巾区域推出两种活动:
活动一:购物满100元送30元券,满200元送60元券,...,上不封顶,送的券当天有效,一次性用完.
活动二:所有商品打8折.
注:两种活动不能同时参加.

素材2
晓琳家用的两种纸巾信息(超市标价).

素材3
晓琳家平均三天用1包清风牌纸巾,平均五天用1包4D溶纸巾;晓琳家清风牌纸巾还有1袋存货,4D溶纸巾存货不清楚.
问题解决
任务1
半年(按180天计算),试求出需要消耗清风牌纸巾多少袋?消耗4D溶纸巾多少箱?
任务2
按存半年的量计算,还需要购买2种纸巾,其中4D溶纸巾x箱,若选择活动二,则所需的总费用为 元(用含x的代数式表示).
任务3
晓琳突然想起4D溶纸巾没有存货,按半年所需量,请探索送券和打折哪个更优惠?并写出探索过程.
7. 类比乘方运算,我们规定:求n个相同有理数(均不为0)的商的运算叫做除方.例如 , 记作 , 读作“2的引4次商”.一般的,把记作 , 读作“a的引n次商”.(1)、直接写出计算结果:= , =.(2)、归纳:负数的引正奇数次商是数,负数的引正偶数次商是数(填“正或负”);(3)、计算:.8. 概念学习规定:求若干个相同的有理数(均不等于0)的除法运算叫做除方,如2÷2÷2,(-3)÷(-3)÷(-3)÷(-3)等.类比有理数的乘方,我们把2÷2÷2记作2③ , 读作“2的圈3次方”,(-3)÷(-3)÷(-3)÷(-3)记作(-3)④ , 读作“-3的圈4次方”,一般地,把a÷a÷a÷…÷a , (n个a , a≠0)记作
 , 读作“a的圈n次方”.(1)、初步探究:
, 读作“a的圈n次方”.(1)、初步探究: →2④=2÷2÷2÷2=2×××=→
→2④=2÷2÷2÷2=2×××=→
①直接写出计算结果:2③= , =;
②关于除方,下列说法错误的是
A.任何非零数的圈2次方都等于1; B.对于任何正整数n , 1ⓝ=1;
C.3④=4③ D.负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数.
(2)、深入思考我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?
①试一试:
仿照上面的算式,将下列运算结果直接写成幂的形式.(-3)④= ▲ ;5⑥= ▲ ;= ▲ .
②想一想:将一个非零有理数a的圈n次方写成幂的形式等于 ▲ ;
③算一算:122÷×-÷33 .
二、数轴
-
9.
【阅读理解】
点、、为数轴上三点,如果点在、之间且到的距离是点到的距离倍,那么我们就称点是的奇点.
例如,如图 , 点表示的数为 , 点表示的数为表示的点到点的距离是 , 到点的距离是 , 那么点是的奇点;又如,表示的点到点的距离是 , 到点的距离是 , 那么点就不是的奇点,但点是的奇点.

【知识运用】
如图 , 、为数轴上两点,点所表示的数为 , 点所表示的数为 .
(1)、数所表示的点是的奇点;数所表示的点是的奇点;(2)、如图 , 、为数轴上两点,点所表示的数为 , 点所表示的数为现有一动点从点出发向左运动,到达点停止.点运动到数轴上的什么位置时,、和中恰有一个点为其余两点的奇点?10. 阅读理解:若、、为数轴上三点,若点到的距离是点到的距离倍,我们就称点是【 , 】的好点.
例如,如图 , 点表示的数为 , 点表示的数为表示的点到点的距离是 , 到点的距离是 , 那么点是【 , 】的好点;又如,表示的点到点的距离是 , 到点的距离是 , 那么点就不是【 , 】的好点,但点是【 , 】的好点.

知识运用:如图 , 、为数轴上两点,点所表示的数为 , 点所表示的数为 .
 (1)、数所表示的点是【 , 】的好点;(2)、如图 , 、为数轴上两点,点所表示的数为 , 点所表示的数为现有一只电子蚂蚁从点出发,以个单位每秒的速度向左运动,到达点停止当为何值时,、和中恰有一个点为其余两点的好点?
(1)、数所表示的点是【 , 】的好点;(2)、如图 , 、为数轴上两点,点所表示的数为 , 点所表示的数为现有一只电子蚂蚁从点出发,以个单位每秒的速度向左运动,到达点停止当为何值时,、和中恰有一个点为其余两点的好点? 11. 数轴是一个非常重要的数学工具,它使数和数轴上的点建立起了对应关系,揭示了数与点之间的内在联系
11. 数轴是一个非常重要的数学工具,它使数和数轴上的点建立起了对应关系,揭示了数与点之间的内在联系 (1)、操作一:
(1)、操作一:折叠纸面,若使1表示的点与-1表示的点重合,则-3表示的点与 表示的点重合;
(2)、操作二:折叠纸面,若使1表示的点与3表示的点重合,回答以下问题:
①-3表示的点与数 表示的点重合;
②若数轴上A、B两点之间距离为9(A在B的左侧),且A、B两点经折叠后重合,则A、B两点表示的数分别是 , ;
(3)、操作三:在数轴上剪下9个单位长度(从-1到8)的一条线段,并把这条线段沿某点折叠(如图所示).若得到的这三条线段的长度之比为1:1:2,则折痕处对应的点所表示的数可能是多少?
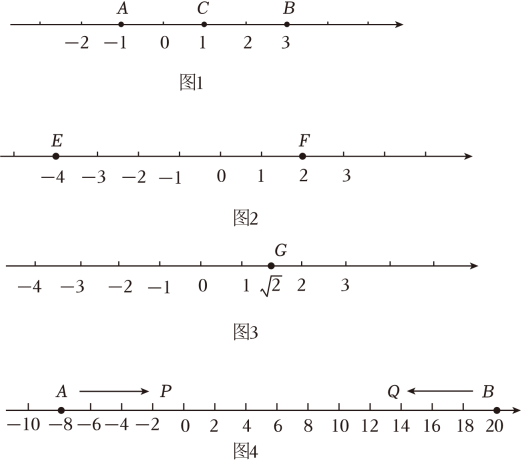
12. 新定义学习:【新知学习】若A,B,C是数轴上的三个点,如果点C到A的距离等于点C到B的距离,那么我们就称点C是AB的中点.例如,如图1,点A表示的数为-1,点B表示的数为3,表示数1的点C到点A的距离是2,到点B的距离是2,那么点C是AB的中点.
 (1)、【知识运用】
(1)、【知识运用】①如图2,E、F为数轴上两点,点E所表示的数为-4,点F所表示的数为2,求EF的中点所表示的数,并说明理由.
②如图3,若数所表示的点G是MN的中点,那么M表示的数为 , N表示的数为 (只要写出符合条件的一对值即可).
(2)、【知识拓展】如图4,A,B为数轴上两点,点A所表示的数为-8,点B所表示的数为20.现有一只电子蜗牛P从点A出发,以1个单位每秒的速度向右运动;同时另一只电子蜗牛Q从点B出发,以2个单位每秒的速度向左运动,若点M,N分别是AP和BQ的中点,则在P,Q的运动过程中,当t=秒时,M,N点到原点的距离相等(请直接写出答案).13. 阅读理解:若、、为数轴上三点,若点到的距离是点到的距离倍,我们就称点是【 , 】的好点.
例如,如图 , 点表示的数为 , 点表示的数为表示的点到点的距离是 , 到点的距离是 , 那么点是【 , 】的好点;又如,表示的点到点的距离是 , 到点的距离是 , 那么点就不是【 , 】的好点,但点是【 , 】的好点.
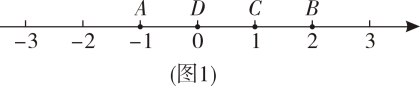
知识运用:如图 , 、为数轴上两点,点所表示的数为 , 点所表示的数为 .
 (1)、数所表示的点是【 , 】的好点;(2)、如图 , 、为数轴上两点,点所表示的数为 , 点所表示的数为现有一只电子蚂蚁从点出发,以个单位每秒的速度向左运动,到达点停止当为何值时,、和中恰有一个点为其余两点的好点?
(1)、数所表示的点是【 , 】的好点;(2)、如图 , 、为数轴上两点,点所表示的数为 , 点所表示的数为现有一只电子蚂蚁从点出发,以个单位每秒的速度向左运动,到达点停止当为何值时,、和中恰有一个点为其余两点的好点?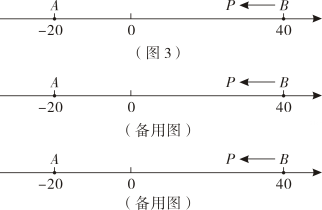 14. 【方法感悟】阅读下面材料:
14. 【方法感悟】阅读下面材料:点A,B在数轴上分别表示实数a,b,A,B两点之间的距离表示为.如图1,从数轴上看,若点A,B表示的分别是1,4则或;
若点A,B表示的数分别是 , 4则或;
若点A,B表示的数分别是 , , 则或 .
【归纳】若点A,B表示的数分别是 , 则或 .
【知识迁移】
(1)、如图1,点A,B表示的数分别是 , b且 , 则;(2)、如图2,点A,B表示的数分别是 , , 若把向左平移个单位,则点A与重合,若把向右平移个单位,则点B与70重合,那么 , ;(3)、【拓展应用】
一天,美羊羊去问村长爷爷的年龄,村长爷爷说:“我若是你现在这么大,你还要40年才出生呢,你若是我现在这么大,我已经是老寿星了,116岁了,哈哈!”美羊羊纳闷,请问村长爷爷现在到底是多少岁?美羊羊现在又是几岁?请写出解题思路.(4)、结合几何意义,求最小值.
三、实数
-
15. 教材上有这样一个合作学习活动:如图1,依次连结2×2方格四条边的中点A , B , C , D , 得到一个阴影正方形.设每一小方格的边长为1,得到阴影正方形面积为2.
 (1)、【基础尝试】:
(1)、【基础尝试】:发现图1这个阴影正方形的边长就是小方格的对角线长,则小方格对角线长是 , 由此我们得到一种在数轴上找到无理数的方法;
(2)、【画图探究】:如图2,以1个单位长度为边长画一个正方形,以数字1所在的点为圆心,正方形的对角线为半径画弧,与数轴交于M , N两点,则点M表示的数为;
(3)、【问题解决】:如图3,3×3网格是由9个边长为1的小方格组成.
①画出面积是5的正方形,使它的顶点在网络的格点上;
②请借鉴(2)中的方法在数轴上找到表示实数的准确位置.(保留作图痕迹并标出必要线段长)
16. 如图①,把两个边长为的小正方形沿对角线剪开,所得的个直角三角形拼成一个面积为的大正方形.由此得到了一种能在数轴上画出无理数对应点的方法.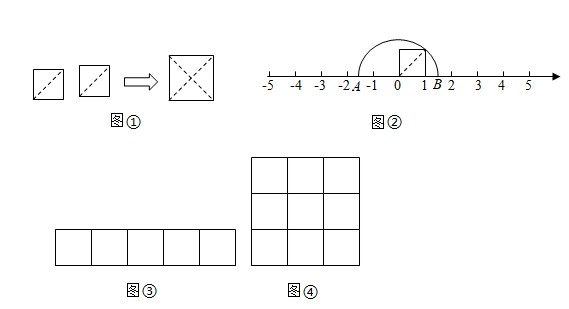 (1)、图②中、两点表示的数分别为 , ;(2)、请你参照上面的方法:
(1)、图②中、两点表示的数分别为 , ;(2)、请你参照上面的方法:把图③中的长方形进行剪裁,并拼成一个大正方形.在图③中画出裁剪线,并在图④的正方形网格中画出拼成的大正方形,该正方形的边长 ▲ . (注:小正方形边长都为 , 拼接不重叠也无空隙)
17. 如图,有这样一个探究:把两个边长为1的小正方形分别沿对角线剪开,将所得的4个直角三角形拼在一起,可以得到一个面积为2的大正方形,试根据这个研究方法回答下列问题: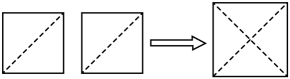 (1)、所得到的面积为2的大正方形的边长就是原边长为1的小正方形的对角线长,因此可得小正方形的对角线长为;(2)、由此我们得到一种在数轴上找到无理数的方法:如下图,以单位长度为边长画一个正方形,以数字1所在的点为圆心,正方形的对角线为半径画弧,与数轴交于、两点,那么点表示的数为;
(1)、所得到的面积为2的大正方形的边长就是原边长为1的小正方形的对角线长,因此可得小正方形的对角线长为;(2)、由此我们得到一种在数轴上找到无理数的方法:如下图,以单位长度为边长画一个正方形,以数字1所在的点为圆心,正方形的对角线为半径画弧,与数轴交于、两点,那么点表示的数为;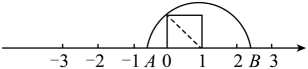 (3)、通过动手操作,漠子同学把长为5,宽为1的长方形进行裁剪,拼成如图所示的正方形.请借鉴(2)中的方法在数轴上找到表示的点 . (保留作图痕迹并标出必要线段长)
(3)、通过动手操作,漠子同学把长为5,宽为1的长方形进行裁剪,拼成如图所示的正方形.请借鉴(2)中的方法在数轴上找到表示的点 . (保留作图痕迹并标出必要线段长)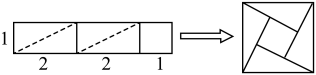
 18. 阅读下列信息材料:
18. 阅读下列信息材料:信息1:因为无理数是无限不循环小数,因此无理数的小数部分我们不可能全部地写出来比如:π、等,而常用的“…”或者“≈”的表示方法都不够百分百准确;
信息2:2.5的整数部分是2,小数部分是0.5,可以看成2.5﹣2得来的;
信息3:任何一个无理数,都可以夹在两个相邻的整数之间,如2<<3,是因为;
根据上述信息,回答下列问题:
(1)、的整数部分是 , 小数部分是;(2)、8+也是夹在相邻两个整数之间的,可以表示为a<8+<b则a+b=;(3)、若-2=a+b,其中a是整数,且0<b<1,请求2a-b的相反数.19. 教材上有这样一个合作学习活动:如图1,依次连结2×2方格四条边的中点A , B , C , D , 得到一个阴影正方形.设每一小方格的边长为1,得到阴影正方形面积为2. (1)、【基础尝试】
(1)、【基础尝试】发现图1这个阴影正方形的边长就是小方格的对角线长,则小方格对角线长是 , 由此我们得到一种在数轴上找到无理数的方法;
(2)、【画图探究】如图2,以1个单位长度为边长画一个正方形,以数字1所在的点为圆心,正方形的对角线为半径画弧,与数轴交于M , N两点,则点M表示的数为;
(3)、【问题解决】如图3,3×3网格是由9个边长为1的小方格组成.
①画出面积是5的正方形,使它的顶点在网络的格点上;
②请借鉴(2)中的方法在数轴上找到表示实数的准确位置.(保留作图痕迹并标出必要线段长)

四、一元一次方程
-
20. 每年“双十一”购物节,商家都会利用这个契机进行促销活动.今年某超市也有促销活动,小明一家去逛该超市,准备购买纸巾,根据以下素材,探索完成任务.
素材1 纸巾区域推出两种活动:活动一:购物满100元送25元券,满200元送50元券,满300元送75元券,…,上不封顶,送的券当天有效,一次性用完.
活动二:所有商品打8.5折.(注:两种活动不能同时参加)
素材2 小明家用的两种纸巾信息(超市标价)

素材3 小明家平时同时使用这两种纸巾,平均三天用1包清风牌纸巾,平均五天用1包4D溶纸巾;小明家清风牌纸巾还有1袋存货,4D溶纸巾存货不清楚.
(1)、任务1 半年(按180天计算),试求出需要消耗清风牌纸巾多少袋?消耗4D溶纸巾多少箱?(2)、任务2 按存半年的量计算,还需要购买2种纸巾,其中4D溶纸巾x箱,若选择活动二,则所需的总费用为元(用含x的代数式表示);(3)、任务3 小明突然想起4D溶纸巾没有存货,按半年所需量,请探索送券和打折哪个更优惠?并写出探索过程.21.
问题解决怎么做出更多的纸盒 素材1 如右图,用4个长方形纸板作侧面,1个正方形纸板作底面可以做成1个竖式无盖纸盒 
素材2 如右图,用2个长方形纸板与2个正方形纸板作侧面,1个长方形纸板作底面可以做成1横式无盖纸盒 
素材3 现有200张长方形纸板与100张正方形纸板 (1)、问题1 若要使做成的竖式无盖纸盒与横式无盖纸盒的数量一样多,则最多可以做成多少个无盖纸盒(两种纸盒之和)?(2)、问题2 若要使做成的竖式无盖纸盒比横式无盖纸盒多10个,则最多可以做成多少个无盖纸盒(两种纸盒之和)?(3)、问题3 若要先做出10个竖式无盖纸盒,接着再做竖式无盖纸盒或横式无盖纸盒,则最后最多可以做成个无盖纸盒(两种纸盒之和,包括先做出的10个纸盒)?(直接写答案)