《有理数、实数及其运算》精选压轴题—2024年浙教版数学七（上）期中复习

试卷更新日期：2024-10-19 类型：复习试卷

进入出卷网下载

一、选择题

1. 我国古代《易经》一书中记载，远古时期，人们通过在绳子上打结来记录数量，即“结绳计数”，如图，一位母亲在从右到左依次排列的绳子上打结，满八进一，用来记录孩子自出生后的天数．由图可知，孩子自出生后的天数是（）

A、336 B、510 C、726 D、1326

查看试题解析
2. 已知a是 $\sqrt{26} - 2$ 的整数部分，b是 $\sqrt{26} - 2$ 的小数部分，则 ${(- a + 2)}^{3} + {(b + 5)}^{2}$ 的平方根是（）

A、3 B、±3 C、5 D、±5

查看试题解析
3. 已知a₁+a₂＝1，a₂+a₃＝2，a₃+a₄＝ $- 3$ ， a₄+a₅＝ $- 4$ ， a₅+a₆＝5，a₆+a₇＝6，a₇+a₈＝ $- 7$ ， a₈+a₉＝ $- 8$ ， ……，a₉₉+a₁₀₀＝ $- 99$ ， a₁₀₀+a₁＝ $- 100$ ，那么a₁+a₂+a₃+……+a₁₀₀的值为（）

A、﹣48 B、﹣50 C、﹣98 D、﹣100

查看试题解析
4. 电子跳蚤游戏盘（如图）为△ABC，AB=10，BC=11，AC=12。如果电子跳蚤开始时在BC边上的P₀点，BP₀=4，第一步跳蚤跳从 $P_{0}$ 跳到 $A C$ 边上 $P_{1}$ 点，且CP₁=CP₀；第二步跳蚤从P₁跳到AB边上P₂点，且AP₂=AP₁；第三步跳蚤从P₂跳回到BC边上P₃点，且BP₃=BP₂……跳蚤按上述规则跳下去，第n次落点为P_n ，则P₄与P₂₀₂₃之间的距离是（）.

A、0 B、1 C、4 D、5

查看试题解析
5. 观察图1、图2、图3的运算过程并找出规律：
求的值为（）

A、8 B、-8 C、-32 D、32

查看试题解析
6. 若2023个数 $a_{1}$ 、 $a_{2}$ 、 $a_{3}$ 、 $⋯$ 、 $a_{2023}$ 满足下列条件： $a_{1} = 2 ， a_{2} = - | a_{1} + 5 |$ ， $a_{3} = - | a_{2} + 5 | ， ⋯ ， a_{2023} = - | a_{2022} + 5 |$ ，则 $a_{1} + a_{2} + a_{3} + ⋯ + a_{2023} =$ （）

A、 $- 5057$ B、 $- 5055$ C、 $- 5051$ D、 $- 5050$

查看试题解析

二、填空题

7. 某校园餐厅把WIFI密码做成了数学题，小亮在餐厅就餐时，思索了一会，输入密码，顺利地连接到了学子餐厅的网络，那么他输入的密码是．

查看试题解析
8. 一个数值转换器，如图所示：
（1）当输入的x为16时．输出的y值是；
（2）若输出的y是 $\sqrt{3}$ ，请写出两个满足要求的x值：．

查看试题解析
9. 规定如下两种运算： $x \otimes y = 2 x y + 1$ ； $x \oplus y = x + 2 y - 1$ ．例如： $2 \otimes 3 = 2 \times 2 \times 3 + 1 = 13$ ； $2 \oplus 3$ $= 2 + 2 \times 3 - 1 = 7$ ．若 $a \otimes (4 \oplus 5)$ 的值为79，则 $a =$

查看试题解析
10. 已知整数a，b，c，且 $c < 0$ ，满足 $| a | + 10 b^{2} - 100 c^{3} = 2023$ ，则 $a + b + c$ 的最小值为.

查看试题解析
11. 按一定规律排列的一列数依次为： $3 ， - \frac{5}{3} ， \frac{9}{5} ， - \frac{17}{7} ， \frac{33}{9} ， - \frac{65}{11} ， … …$ 按此规律排列下去，第10个数是.

查看试题解析
12. 若 $\sqrt{a - 2023} +$ |b+2023|﹣1＝0，其中a ， b均为整数，则a+b＝．

查看试题解析
13. 做一个数字游戏．第一步：取一个自然数 $n_{1} = 5$ ，计算 $n_{1}^{2} + 1$ 得 $a_{1}$ ；第二步：算出 $a_{1}$ 的各位数字之和得 $n_{2}$ ，计算 $n_{2}^{2} + 1$ 得 $a_{2}$ ；第三步：算出 $a_{2}$ 的各位数字之和得 $n_{3}$ ，计算 $n_{3}^{2} + 1$ 得 $a_{3}$ ；…则 $a_{3} =$ ．依此类推，则 $a_{2023} =$ ．

查看试题解析
14. 如图，是一个数值转换器，其工作原理如图所示．

(1)、当输入的x值为5时，则输出的y值为；

(2)、若输出的y是 $\sqrt{7}$ 且10≤|x|＜100，则输入的x的值为．

查看试题解析
15. 根据图中的程序，当输入x为64时，输出的值是．

查看试题解析
16. 观察下列式子，并回答问题：
$\begin{array}{l} 1^{3} = \frac{1}{4} \times 1^{2} \times 2^{2} \\ 1^{3} + 2^{3} = \frac{1}{4} \times 2^{2} \times 3^{2} \\ 1^{3} + 2^{3} + 3^{3} = \frac{1}{4} \times 3^{2} \times 4^{2} \\ 1^{3} + 2^{3} + 3^{3} + 4^{3} = \frac{1}{4} \times 4^{2} \times 5^{2} \\ ⋯ ⋯ \end{array}$
请计算： $\begin{array}{l} 7^{3} {+8}^{3} {+9}^{3} {+⋯+19}^{3} \end{array}$ =.

查看试题解析
17. 如图，面积为3的正方形 $A B C D$ 的顶点A在数轴上，对应的数为1，以点A为圆心， $A D$ 长为半径画弧交数轴于点E（点E位于点A的左侧），则线段 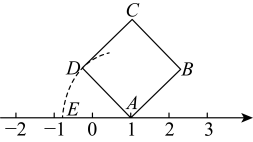$E A =$ ，点E对应的数为．

查看试题解析
18. 在草稿纸上计算：① $\sqrt{1^{3}}$ ；② $\sqrt{1^{3} + 2^{3}}$ ；③ $\sqrt{1^{3} + 2^{3} + 3^{3}}$ ；④ $\sqrt{1^{3} + 2^{3} + 3^{3} + 4^{3}}$ ，观察你计算的结果，用你发现的规律直接写出下面式子的值 $\sqrt{1^{3} + 2^{3} + 3^{3} + \dots + 28^{3}}$ = ．

查看试题解析
19. 观察下列算式： $2^{1} = 2 、 2^{2} = 4 、 2^{3} = 8 、 2^{4} = 16 、 2^{5} = 32 、 2^{6} = 64, 2^{7} = 128, 2^{8} = 256$ ，根据规律，则 $2^{2022}$ 的末位数字是．

查看试题解析

三、解答题

20. 观察下列各式：
$3^{2} - 3^{1} = 2 \times 3^{1}$ ①
$3^{3} - 3^{2} = 2 \times 3^{2}$ ②
$3^{4} - 3^{3} = 2 \times 3^{3}$ ③
……
探索以上式子的规律：

(1)、写出第5个等式：______；

(2)、试写出第 $n$ 个等式：______；

(3)、由已知这个等式 $3^{2} - 3^{1} = 2 \times 3^{1}$ 可以转化为 $3^{1} = \frac{3^{2} - 3^{1}}{2}$ ，同样 $3^{3} - 3^{2} = 2 \times 3^{2}$ 可以转化为 $3^{2} = \frac{3^{3} - 3^{2}}{2}$ ，根据这个规律第 $n$ 个等式可以转化为：______；

(4)、计算 $3^{1} + 3^{2} + 3^{3} + \dots + 3^{2023}$ ．

查看试题解析
21.
【概念学习】
规定：求若干个相同的有理数（均不等于0）的除法运算叫做除方，如 $2 \div 2 \div 2$ 等，类比有理数的乘方，我们把 $2 \div 2 \div 2$ 记作 $2^{③}$ ，读作“2的圈3次方”．
（1）直接写出计算结果： $2^{③} =$ ___________， ${(\frac{1}{3})}^{③} =$ ___________．
【深入思考】
我们知道，有理数的减法运算可以转化为加法运算，除法运算可以转化为乘法运算，有理数的除方运算如何转化为乘方运算呢？例如：
$2^{④} = 2 \div 2 \div 2 \div 2$
$= 2 \times \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}$ （幂的形式）
（2）试一试：将 $5^{⑥}$ 通过除方运算转化成幂的形式，请写出运算过程．
（3）算一算： ${(- \frac{1}{4})}^{③} \div 2^{3} + (- 2) \times 3^{②}$ ．

查看试题解析
22. 教材上有这样一个合作学习活动：如图1，依次连结2×2方格四条边的中点A ， B ， C ， D ，得到一个阴影正方形．设每一小方格的边长为1，得到阴影正方形面积为2．

(1)、【基础尝试】：
发现图1这个阴影正方形的边长就是小方格的对角线长，则小方格对角线长是，由此我们得到一种在数轴上找到无理数的方法；

(2)、【画图探究】：
如图2，以1个单位长度为边长画一个正方形，以数字1所在的点为圆心，正方形的对角线为半径画弧，与数轴交于M ， N两点，则点M表示的数为；

(3)、【问题解决】：
如图3，3×3网格是由9个边长为1的小方格组成．
①画出面积是5的正方形，使它的顶点在网络的格点上；
②请借鉴（2）中的方法在数轴上找到表示实数 $\sqrt{5} - 1$ 的准确位置．（保留作图痕迹并标出必要线段长）

查看试题解析
23. 如图，在 $4 \times 4$ 的小正方形组成的图形中有一个阴影部分（阴影部分也是正方形）．若每个小正方形的边长为1，点A表示的数为1．

(1)、图中正方形 $A B C D$ 的面积为多少？它的边长为多少？这个值在哪两个连续整数之间？

(2)、若阴影正方形的边长的值的整数部分为x，小数部分为y，求 $(y - \sqrt{10})^{x}$ 的值，

(3)、若正方形 $A B C D$ 从当前状态沿数轴正方向翻滚，我们把点B滚到与数轴上的点P重合时，记为第一次翻滚，如图所示，C翻滚到数轴上时，记为第二次翻滚，以此类推，请直接回答：
①点P表示的数为多少？
②是否存在正整数n，使得该正方形n次翻滚后，其顶点A，B，C，D中的某个点与2023重合？

查看试题解析