《数轴》精选压轴题—2024年浙教版数学七（上）期中复习

试卷更新日期：2024-10-19 类型：复习试卷

进入出卷网下载

一、选择题

1. 有理数 $a$ ， $b$ ， $c$ 在数轴上的位置如图所示：
$① a b c < 0$ ； $② （ a - b ）（ b - c ）（ c - a ） < 0$ ； $③ | b | < 2 - a c$ ； $④ | a - c | + | a - b | = | b - c |$ ．以上 $4$ 个结论正确的有（）

A、 $1$ 个 B、 $2$ 个 C、 $3$ 个 D、 $4$ 个

查看试题解析
2. 如图，数轴上A ， B ， C三点表示的数分别为a ， b ， c ， ①若a＝﹣2，b＝3，c＝8则AB+BC＝6；②化简|c﹣b|+|a﹣b|﹣|a﹣c|＝2c；③若数轴上点M到A ， B ， C距离之和最小，则点M与点B重合；④若a＝﹣2，b＝0，c＝4点M到A ， B ， C的距离之和为13，则点M表示的数为5；⑤若（|a+2|+|a﹣1|）（|b﹣2|+|b﹣5|）（|c﹣6|+|c﹣10|）＝36，则2a+3b+4c最小值为26．则结论正确的个数是（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

3. 如图，数轴上A、B两点之间的距离为20，有一根木棒MN（M在N的左侧），当N移动到与A、B其中一个端点重合时，点M所对应的数为8，点N到AB中点时，点M所对应的数为．

查看试题解析
4. 等边△ABC在数轴上的位置如图所示，点A、C对应的数分别为0和-1，若△ABC绕顶点按顺时针方向在数轴上连续翻转，翻转1次后，点B所对应的数为1，则连续翻转2023次后，点B对应的数是．

查看试题解析

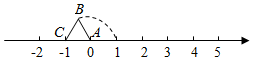
三、解答题

5. 数轴是一个非常重要的数学工具，它使数和数轴上的点建立起对应关系，揭示了数与点之间的内在联系，它是“数形结合”的基础．
【阅读】|3﹣1表示3与1差的绝对值，也可理解为3与1两数在数轴上所对应的两点之间的距离；|3+1|可以看作|3﹣（﹣1）|，表示3与﹣1的差的绝对值，也可理解为3与﹣1两数在数轴上所对应的两点之间的距离．

(1)、若在数轴上点A表示数a，点B表示数b，a、b满足|a+2|+（b﹣4）²＝0．点A表示的数为；点B表示的数为；

(2)、利用数轴，找出所有符合条件的整数x，若使得|x﹣（﹣1）|＝3，则x＝；

(3)、在（1）的条件下，若P为数轴上一点，P到A，B的距离之和为7，则点P所对应的数是；

(4)、【动手折一折】若1表示的点和﹣1表示的点重合，则2表示的点与﹣2表示的点重合；若3表示的点和﹣1表示的点重合，则5表示的点和表示的点重合；这时如果E、F两点之间的距离为6（E在F的左侧）且E、F两点经折叠后重合，则点E表示的数是．

查看试题解析
6. 如图，点O为数轴的原点，点A表示的数为7，边长为1的正方形BCDE在数轴上，此时点C在点A左边，且点C与点A的距离为2．

(1)、写出数轴上点B表示的数为.

(2)、若正方形BCDE以每秒1个单位长度的速度沿数轴向右运动，同时点P以每秒3个单位长度从原点出发沿数轴向右运动．
①当P，B两点相遇时，请求出此时点C在数轴上表示的数．
②在整个运动过程中，当点P遇到点B时，立即以原速度沿数轴向左运动．若点C与点A的距离等于点P到点O的距离，此时P在数轴上表示的数为． (直接写出答案即可)

查看试题解析
7. 在数轴上点A表示的数是6，点B位于点A的左侧，与点A的距离是12个单位长度．

(1)、点B表示的数是．

(2)、动点P从点B出发，沿着数轴向右以每秒2个单位长度的速度运动．经过多少秒，点P到AB的距离相等．

(3)、在（2）的条件下，点P出发的同时，点Q也从点A出发，沿着数轴向左，以每秒1个单位长度的速度运动．经过多少秒，点Q到点B的距离是点P到点A距离的2倍？

查看试题解析
8. 如图数轴上有两个点 $A$ 、 $B$ ，分别表示的数是 $- 2$ ， $4 .$ 请回答以下问题：

(1)、 $A$ 与 $B$ 之间距离为， $A$ ， $B$ 中点对应的数为， $B$ 点向左平移 $9$ 个单位对应的数为．

(2)、若点 $C$ 对应的数为 $- 5$ ，只移动 $C$ 点，要使得 $A$ ， $B$ ， $C$ 其中一点到另两点之间的距离相等，请写出所有的移动方法．

(3)、若点 $P$ 从 $A$ 点出发，以每秒 $1$ 个单位长度的速度向左作匀速运动，点 $Q$ 从 $B$ 出发，以每秒 $3$ 个单位长度的速度向左作匀速运动， $P$ ， $Q$ 同时运动：
$①$ 当点 $P$ 运动多少秒时，点 $P$ 和点 $Q$ 重合？
$②$ 当点 $P$ 运动多少秒时， $P$ ， $Q$ 之间的距离为 $2$ 个单位长度？

查看试题解析
9. 对于数轴上不同的三点A，B，C，给出如下定义：若其中一个点与其它两个点的距离恰好相等，则称该点是其它两个点的“等距点”．例如：数轴上点A，B，C所表示的数分别为1，3，5，此时数轴上点B与点A之间的距离是2，点B与点C之间的距离是2，所以B是A，C的“等距点”．

(1)、若点A表示数-2，点B表示的数2，下列各数 $- \frac{2}{3}$ ， 0，4，6所对应的点分别C₁ ， C₂ ， C₃ ， C₄ ，其中是点A，B的“等距点”的是．

(2)、点A表示数-1，点B表示的数3，P为数轴上一个动点，若A、B、P中有一个点恰好是其它两个点的“等距点”，求此时点P表示的数．

(3)、数轴上点A所表示的数为-10，点B所表示的数为20，一只电子蚂蚁P从点B出发，以2个单位每秒的速度沿数轴向左运动，同时另一只电子蚂蚁Q从点A出发，以1个单位每秒的速度沿数轴向右运动，设运动时间为t秒．问：当t为何值时，P、Q、B三个点中恰有一个点为其余两点的“等距点”？（直接写出t的值）

查看试题解析
10. 【背景知识】数轴是初中数学学习的一个重要工具，利用数轴可以将数与形完美地结合．研究数轴我们发现了许多重要的规律，例如：若数轴上点A，B分别对应数a， B．则A，B两点之间的距离为 $A B = | a - b |$ ．
【问题情境】如图，数轴上点A，B分别对应数a， B．其中 $a < 0 ， b > 0$ ．
【综合运用】

(1)、当 $a = - 8 ， b = 2$ 时，线段AB的长度是；

(2)、若该数轴上另有一点N对应着数n．
①在（1）的条件下，若点N在点A，B之间，且满足 $N A = 4 N B$ ，则数n是 ▲ ；
②当 $b = 3$ ，且 $B N = 3 A N$ 时，探究a与n之间的数量关系．

查看试题解析
11. 定义：若A、B、C为数轴上三个不同的点，若点C到点A的距离和点C到点B的距离的2倍的和为16，我们就称点C是[A ， B]的友好点．例如：点M、N、P表示的数分别为﹣8、4、0，则点P到点M的距离是8，到点N的距离是4，那么点P是[M ， N]的友好点，而点P就不是[N ， M]的友好点．

(1)、若点M、N、P表示的数分别为3、9、14，则是[ ， ]的友好点．（空格内分别填入M、N、P）

(2)、若点M、P表示的数分别为﹣6、﹣2，且P是[M ， N]的友好点，则点N为．

(3)、如图，数轴上A ， B ， C三点分别表示的数为﹣10、12、2，点Q从B点出发以每秒12个单位长度的速度沿数轴向左匀速运动，当它到达A点后立即以相同的速度返回往B点运动，并持续在A ， B两点间往返运动．在Q点出发的同时，点P从A点出发以每秒3个单位长度向右匀速运动，直到当点P达到C点时，点P ， Q停止运动．当t为何值时，点C恰好为[P ， Q]的友好点？

查看试题解析
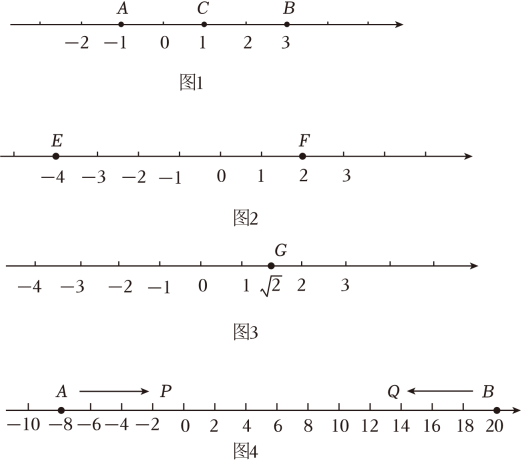
12. 新定义学习：
【新知学习】若A，B，C是数轴上的三个点，如果点C到A的距离等于点C到B的距离，那么我们就称点C是AB的中点．例如，如图1，点A表示的数为-1，点B表示的数为3，表示数1的点C到点A的距离是2，到点B的距离是2，那么点C是AB的中点．

(1)、【知识运用】
①如图2，E、F为数轴上两点，点E所表示的数为-4，点F所表示的数为2，求EF的中点所表示的数，并说明理由．
②如图3，若数 $\sqrt{2}$ 所表示的点G是MN的中点，那么M表示的数为， N表示的数为（只要写出符合条件的一对值即可）．

(2)、【知识拓展】如图4，A，B为数轴上两点，点A所表示的数为-8，点B所表示的数为20．现有一只电子蜗牛P从点A出发，以1个单位每秒的速度向右运动；同时另一只电子蜗牛Q从点B出发，以2个单位每秒的速度向左运动，若点M，N分别是AP和BQ的中点，则在P，Q的运动过程中，当t＝秒时，M，N点到原点的距离相等（请直接写出答案）．

查看试题解析
13. 已知式子 $M = (a + 4) x^{3} + 6 x^{2} - 2 x + 5$ 是关于 $x$ 的二次多项式，且二次项系数为 $b$ ，数轴上 $A$ ， $B$ 两点所对应的数分别是 $a$ 和 $b$ ．

(1)、则 $a =$ ， $b =$ ； $A$ ， $B$ 两点之间的距离为；

(2)、有一动点 $P$ 从点 $A$ 出发第一次向左运动1个单位长度，然后在新的位置第二次向右运动2个单位长度，再在此位置第三次向左运动3个单位长度…，按照如此规律不断地左右运动，当运动到第2023次时，求点 $P$ 所对应的有理数；

(3)、若点 $A$ 以每秒3个单位长度的速度向左运动，同时点 $B$ 以每秒5个单位长度的速度向右运动，动点 $D$ 从原点开始以每秒 $m (m > 0)$ 个单位长度在 $A ， B$ 之间运动（到达 $A$ 或 $B$ 即停止运动），运动时间为 $t$ 秒，在运动过程中， $B D - 2 A D$ 的值始终保持不变，求 $D$ 点运动的方向及 $m$ 的值．

查看试题解析
14. 数轴是一个非常重要的数学工具，它使数和数轴上的点建立起了对应关系，揭示了数与点之间的内在联系

(1)、操作一：
折叠纸面，若使1表示的点与-1表示的点重合，则-3表示的点与表示的点重合；

(2)、操作二：
折叠纸面，若使1表示的点与3表示的点重合，回答以下问题：
①-3表示的点与数表示的点重合；
②若数轴上A、B两点之间距离为9（A在B的左侧），且A、B两点经折叠后重合，则A、B两点表示的数分别是，；

(3)、操作三：
在数轴上剪下9个单位长度（从-1到8）的一条线段，并把这条线段沿某点折叠（如图所示）．若得到的这三条线段的长度之比为1：1：2，则折痕处对应的点所表示的数可能是多少？

查看试题解析
15. 如图，数轴上有 $A$ 、 $B$ 、 $C$ 三个点，分别表示数 $- 18$ 、 $- 10$ 、 $20$ ，有两条动线段 $P Q$ 和 $M N ($ 点 $Q$ 与点 $A$ 重合，点 $N$ 与点 $B$ 重合，且点 $P$ 总在点 $Q$ 的左边，点 $M$ 总在点 $N$ 的左边 $)$ ， $P Q = 2$ ， $M N = 5$ ，线段 $M N$ 以每秒 $1$ 个单位的速度从点 $B$ 开始一直向右匀速运动，同时线段 $P Q$ 以每秒 $3$ 个单位的速度从点 $A$ 开始向右匀速运动．当点 $Q$ 运动到点 $C$ 时，线段 $P Q$ 立即以相同的速度返回；当点 $P$ 运动到点 $A$ 时，线段 $P Q$ 、 $M N$ 立即同时停止运动．设运动时间为 $t$ 秒 $($ 整个运动过程中，线段 $P Q$ 和 $M N$ 保持长度不变 $)$ ．

(1)、当 $t = 2$ 时，点 $Q$ 表示的数为______，点 $M$ 表示的数为______．

(2)、当开始运动后， $t =$ ______秒时，点 $Q$ 和点 $C$ 重合．

(3)、在整个运动过程中，求点 $Q$ 和点 $N$ 重合时 $t$ 的值．

(4)、在整个运动过程中，当线段 $P Q$ 和 $M N$ 重合部分长度为 $1$ 时，请直接写出此时 $t$ 的值．

查看试题解析
16. 数轴是一个非常重要的数学工具，它使数和数轴上的点建立起对应关系，揭示了数与点之间的内在联系，它是“数形结合”的基础．
【阅读】 $| 3 - 1 |$ 表示3与1差的绝对值，也可理解为3与1两数在数轴上所对应的两点之间的距离； $| 3 + 1 |$ 可以看做 $| 3 - (- 1) |$ ，表示3与－1的差的绝对值，也可理解为3与－1两数在数轴上所对应的两点之间的距离．

(1)、若在数轴上点A表示数a ，点B表示数b，a、b满足 $| a + 2 | + (b - 4)^{2} = 0$ ．点A表示的数为；点B表示的数为；

(2)、利用数轴，找出所有符合条件的整数 $x$ ，若使得 $| x - (- 1) | = 3$ ，则 $x$ = ；

(3)、在（1）的条件下，若 P为数轴上一点，P到A ， B的距离之和为7，则点P所对应的数是

(4)、【动手折一折】若1表示的点和 $- 1$ 表示的点重合，则2表示的点与 $- 2$ 表示的点重合；若3表示的点和 $- 1$ 表示的点重合，则5表示的点和表示的点重合；这时如果E、F两点之间的距离为6（E在F的左侧）且E、F两点经折叠后重合，则点E表示的数是.

查看试题解析
17. 数轴上有A、B两点，分别对应的数为a ， b ，已知（a+2）²与|b-6|互为相反数．点P为数轴上一动点，对应的数为x ．

(1)、若点P到点A和点B的距离相等，求点P对应的数；

(2)、数轴上是否存在点P ，使点P到点A和点B的距离之和为10？若存在，请求出x的值；若不存在，说明理由；

(3)、当点P以每分钟1个单位长度的速度从O点向左运动，点A以每分钟5个单位长度向左运动，点B以每分钟20个单位长度的速度向左运动，问几分钟时点P到点A、点B的距离相等？

查看试题解析