《代数式》精选压轴题—2024年浙教版数学七（上）期中复习

试卷更新日期：2024-10-19 类型：复习试卷

进入出卷网下载

一、选择题

1. 历史上，数学家欧拉最先把关于 $x$ 的多项式用记号 $f (x)$ 来表示，把 $x$ 等于某数 $a$ 的多项式的值用 $f (a)$ 来表示．例如x=-3时，多项式 $f (x) = - 3 x^{2} + x$ 的值记为 $f (- 3)$ ，那么 $f (- 3)$ 的值等于（）

A、-30 B、-27 C、24 D、30

查看试题解析
2. 如图，在一个大长方形中放入三个边长不等的小正方形①、②、③，若要求出两个阴影部分周长的差，只要知道下列哪个图形的面积（）

A、正方形① B、正方形② C、正方形③ D、大长方形

查看试题解析
3. 有一个数值转换器，原理如图所示，若开始输入 $x$ 的值是5，则第1次输出的结果是16，第2次输出的结果是8，第3次输出的结果是4．依次继续下去，第2023次输出的结果是（）

A、8 B、4 C、2 D、5

查看试题解析
4. 把四张大小相同的长方形卡片（如图①）按图②、图③两种放法放在一个底面为长方形（长比宽多6）的盒底上，底面未被卡片覆盖的部分用阴影表示，若记图②中阴影部分的周长为 $C_{2}$ ，图③中阴影部分的周长为 $C_{3}$ ，则 $C_{2} - C_{3}$ 的值为（）

A、10 B、11 C、12 D、13

查看试题解析
5. 如图，一个正方形盒底放了3张完全一样的长方形卡片（卡片不重叠，无缝隙），已知长方形卡片较短边的长度为a ，则未被长方形卡片覆盖的A区域与B区域的周长差是（）

A、4a B、5a C、6a D、8a

查看试题解析
6. 已知a₁+a₂＝1，a₂+a₃＝2，a₃+a₄＝ $- 3$ ， a₄+a₅＝ $- 4$ ， a₅+a₆＝5，a₆+a₇＝6，a₇+a₈＝ $- 7$ ， a₈+a₉＝ $- 8$ ， ……，a₉₉+a₁₀₀＝ $- 99$ ， a₁₀₀+a₁＝ $- 100$ ，那么a₁+a₂+a₃+……+a₁₀₀的值为（）

A、﹣48 B、﹣50 C、﹣98 D、﹣100

查看试题解析
7. 已知有2个完全相同的边长为a、b的小长方形和1个边长为m、n的大长方形，小明把这2个小长方形按如图所示放置在大长方形中，小明经过推理得知，要求出图中阴影部分的周长之和，只需知道a、b、m、n中的一个量即可，则要知道的那个量是（）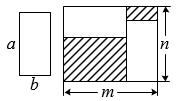

A、a B、b C、m D、n

查看试题解析
8. 下面每个正方形中的五个数之间都有相同的规律，根据这种规律，则第100个正方形的中间数字为（）

A、803 B、797 C、794 D、807

查看试题解析
9. 若2023个数 $a_{1}$ 、 $a_{2}$ 、 $a_{3}$ 、 $⋯$ 、 $a_{2023}$ 满足下列条件： $a_{1} = 2 ， a_{2} = - | a_{1} + 5 |$ ， $a_{3} = - | a_{2} + 5 | ， ⋯ ， a_{2023} = - | a_{2022} + 5 |$ ，则 $a_{1} + a_{2} + a_{3} + ⋯ + a_{2023} =$ （）

A、 $- 5057$ B、 $- 5055$ C、 $- 5051$ D、 $- 5050$

查看试题解析
10. 当x＝2时，代数式x³+mx³+x-1的值为10，则x＝-2时，x³+mx³+x-1的值为（　　）

A、10 B、-10 C、-11 D、-12

查看试题解析
11. 如图，数轴上A，B，C三点表示的数分别为a，b，c则下列结论正确的个数是（　　）
①若 $a = - 2$ ， $b = 3$ ，则 $A B + B C = 6$ ；②若 $a + c = 2 b$ ，则B为AC的中点；③化简 $|c - b| + |a - b| - |a - c| = 2 c$ ；④若数轴上点M到A，B，C距离之和最小，则点M与点B重合；⑤若 $a = - 2$ ， $b = 0$ ， $c = 4$ 点M到A，B，C的距离之和为13，则点M表示的数为5；⑥若 $(|a + 2| + |a - 1|) (|b - 2| + |b - 5|) (|c - 6| + |c - 10|) = 36$ ，则 $2020 a + 2021 b + 2022 c$ 最小值为12134．

A、3 B、4 C、5 D、6

查看试题解析
12. 如图，一个大正方形的四个角落分别放置了四张大小不同的正方形纸片，其中1号，2号两张正方形纸片既不重叠也无空隙．已知1号正方形边长为a ， 2号正方形边长为b ，则阴影部分的周长是（）

A、2a+2b B、4a+2b C、2a+4b D、3a+3b

查看试题解析
13. 把如图1的两张大小相同的长方形卡片放置在图2与图3中的两个相同大长方形中，已知这两个大长方形的长比宽长 $20 c m$ ，若记图2中阴影部分的周长为 $C_{1}$ ，图3中阴影部分的周长为 $C_{2}$ ，那么 $C_{1} - C_{2} =$ （）
图1 图2 图3

A、 $10 c m$ B、 $20 c m$ C、 $30 c m$ D、 $40 c m$

查看试题解析

二、填空题

14. 有按规律排列的一组单项式：x ， ﹣ $\sqrt{2}$ x² ， $\sqrt{3}$ x³ ， ﹣ $\sqrt{4}$ x⁴ ， $\sqrt{5}$ x⁵ ， …则第10个单项式．

查看试题解析
15. 做一个数字游戏．第一步：取一个自然数 $n_{1} = 5$ ，计算 $n_{1}^{2} + 1$ 得 $a_{1}$ ；第二步：算出 $a_{1}$ 的各位数字之和得 $n_{2}$ ，计算 $n_{2}^{2} + 1$ 得 $a_{2}$ ；第三步：算出 $a_{2}$ 的各位数字之和得 $n_{3}$ ，计算 $n_{3}^{2} + 1$ 得 $a_{3}$ ；…则 $a_{3} =$ ．依此类推，则 $a_{2023} =$ ．

查看试题解析
16. 如图1，一段绳子 $M N$ 上一点 $P$ 满足 $M P = 4$ ，将这段绳子 $M N$ 对折，使 $M$ 与 $N$ 重合（如图2），再沿点 $P$ 剪断，使原绳子 $M N$ 分成三段．

(1)、若 $P N = 6$ ，则剪断后最短的绳子长度为；

(2)、若分成的三段绳子的长度之比为 $1 ： 1 ： 3$ ，则 $P N =$ ．

查看试题解析
17. 如图，长方形 $A B C D$ 长为a，宽为b，若 $S_{1} = S_{2} = \frac{1}{2} (S_{3} + S_{4})$ ，则 $S_{4}$ 等于．（用含a、b的代数式表示）

查看试题解析

三、解答题

18. 已知M＝（a+18）x³﹣6x²+12x+5是关于x的二次多项式，且二次项系数和一次项系数分别为b和c，在数轴上A、B、C三点所对应的数分别是a、b、c，数轴上有一动点P从点A出发，以每秒2个单位长度的速度沿数轴向终点C移动，设移动时间为t秒．

(1)、则a＝___，b＝___，c＝___．

(2)、当点P运动到点B时，点Q从点O出发，以每秒6个单位长度的速度沿数轴在点O和点C之间往复运动，
①求t为何值时，点Q第一次与点P重合？
②当点P运动到点C时，点Q的运动停止，求此时点Q一共运动了多少个单位长度，并求出此时点Q在数轴上所表示的有理数．
③设点P，Q所对应的数分别是m、n，当6＜t＜8时，|c﹣n|+|b﹣m|＝8，求t的值．

查看试题解析
19. 为了加强公民的节水意识，合理利用水资源，某市采取价格调控手段以达到节水的目的，下表是该市自来水收费价格的价目表．
价目表

每月用水量
单价
不超出6立方米的部分
2元/ $米^{3}$
超出6立方米但不超出10立方米的部分
4元/ $米^{3}$
超出10立方米的部分
8元/ $米^{3}$
注：水费按月结算

(1)、若某户居民2月份用水4立方米，则应交水费______元．

(2)、若某户居民3月份用水a立方米（其中 $6 < a < 10$ ），求该用户3月份应交水费．（用含a的整式表示，结果要化成最简形式）

(3)、若某户居民4，5月份共用水15立方米（5月份用水量多于4月份），设4月份用水x立方米，求该户居民4，5月份共交水费（用含x的整式表示，结果要化成最简形式）．

查看试题解析
20. 如图所示是一个长为60cm ，宽为xcm的大方形，该图形中阴影A ， B之外的部分由五块形状、大小完全相同的小长方形组成，且每一块小长方形较短边长为10cm ，根据图中信息完成以下问题：

(1)、①求每块小方形较长边长；
②请说明代数式x﹣30的值一定为正数．

(2)、记图形中阴影部分面积之和为S ．
①请用含x的代数式表示S；
②若x＝50，请判断S的值与五块小长方形面积之和是否相等，请说明理由．

查看试题解析

价目表
每月用水量	单价
不超出6立方米的部分	2元/ $米^{3}$
超出6立方米但不超出10立方米的部分	4元/ $米^{3}$
超出10立方米的部分	8元/ $米^{3}$
注：水费按月结算