精选新定义型题—2024年浙教版数学八（上）期中复习

试卷更新日期：2024-10-19 类型：复习试卷

进入出卷网下载

一、三角形

1. 我们新定义一种三角形：两边平方和等于第三边平方的3倍的三角形叫做常态三角形．例如：某三角形三边长分别是3，6和 $\sqrt{15}$ ，因为3²+6²＝3× $\sqrt{15}$ ²＝45，所以这个三角形是常态三角形．

(1)、若△ABC三边长分别是2，3和 $\sqrt{3}$ ，则此三角形常态三角形（填“是”或“不是”）；

(2)、若Rt△ABC是常态三角形，则此三角形的三边长之比为（请按从小到大排列）；

(3)、如图，Rt△ABC中，∠ACB＝90°，BC＝6，点D为AB的中点，连接CD ，若△BCD是常态三角形，求AC的长。

查看试题解析
2. 我们定义：在一个图形上画一条直线，若这条直线既平分该图形的面积，又平分该图形的周长，我们称这条直线为这个图形的“等分积周线”．

(1)、如图1，在△ABC中，AB=BC，且BC≠AC，请你在图1中作出△ABC的一条“等分积周线”；

(2)、在图1中，过点C能否画出一条“等分积周线”？若能，说出确定的方法；若不能，请说明理由．

(3)、如图2，四边形ABCD中，∠B=∠C=90°，EF垂直平分AD，垂足为F，交BC于点E，已知AB=4，BC=10，CD=6．求证：直线EF为四边形ABCD的“等分积周线”；

(4)、如图3，在△ABC中，AB=BC=7cm，AC=10cm，请你不过△ABC的顶点，画出△ABC的一条“等分积周线”，并说明理由．

查看试题解析
3. 规定：如果一个三角形的三个角分别等于另一个三角形的三个角，那么称这两个三角形互为“等角三角形”．从三角形 $($ 不是等腰三角形 $)$ 一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中一个为等腰三角形，另一个与原来三角形是“等角三角形”，我们把这条线段叫做这个三角形的“等角分割线”．

理解概念（1）如图 $1$ ，在 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ， $C D ⊥ A B$ ，图中“等角三角形”有______组．
概念应用（2）如图 $2$ ，在 $△ A B C$ 中， $C D$ 为角平分线， $∠ A = 40 °$ ， $∠ B = 60 ° .$ 求证： $C D$ 为 $△ A B C$ 的等角分割线．
（3）在 $△ A B C$ 中， $∠ A = 42 °$ ， $C D$ 是 $△ A B C$ 的等角分割线，直接写出 $∠ A C B$ 的度数．

查看试题解析
4. 自定义：若 $a, b, c$ 是 $△ A B C$ 的三边，且满足 $a^{2} + b^{2} = 2 c^{2}$ ，则称 $△ A B C$ 为“美眉三角形”

(1)、你认为等边三角形、直角三角形、等腰三角形、等腰直角三角形中一定是“美眉三角形”的有_____________．

(2)、若 $Rt △ A B C$ 是“美眉三角形”，且斜边 $A B = 2 \sqrt{3}$ ，则该三角形的面积为_____________．

(3)、如图， $△ A B C$ 中， $∠ A B C = 120 °, ∠ A C B = 45 °$ ， P为 $A C$ 边上一点，将 $△ A B P$ 沿直线 $B P$ 进行折叠，点 $A$ 落在点 $D$ 处，连接 $C D, A D$ ．若 $△ A B D$ 为“美眉三角形”，且 $A P = \sqrt{2}$ ，求 $△ P D C$ 的面积．

查看试题解析
5. 定义：若 $a$ ， $b$ ， $c$ 是 $△ A B C$ 的三边，且 $a^{2} + b^{2} = 2 c^{2}$ ，则称 $△ A B C$ 为“方倍三角形”．

(1)、对于①等边三角形，②直角三角形，下列说法一定正确的是________．
A.①一定是“方倍三角形”
B.②一定是“方倍三角形”
C.①②都一定是“方倍三角形”
D.①②都一定不是“方倍三角形”

(2)、若 $Rt △ A B C$ 是“方倍三角形”，且斜边 $A B = \sqrt{6}$ ，则该三角形的面积为________；

(3)、如图， $△ A B C$ 中， $∠ A B C = 120 °$ ， $∠ A C B = 45 °$ ， $P$ 为 $A C$ 边上一点，将 $△ A B P$ 沿直线 $B P$ 进行折叠，点 $A$ 落在点 $D$ 处，连接 $C D$ ， $A D$ ．若 $△ A B D$ 为“方倍三角形”，且 $A P = 2$ ，求 $A D$ 的长．

查看试题解析
6. 我们定义：最大边与最小边的比为5：3的三角形叫做“ $[5 ， 3]$ 型三角形”，最长边称为“弦边”.

(1)、小张认为：等腰三角形不可能是“ $[5 ， 3]$ 型三角形” $.$ 你认为他的说法正确吗？若正确，请说明理由；若不正确，请举出反例；

(2)、若 $△ A B C$ 是“ $[5 ， 3]$ 型三角形”， $∠ A = 30 °$ ， “弦边” $A B = 2$ ，则 $A C =$ ；

(3)、如图，在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $A B = 10 .$ 现将 $△ A B C$ 关于直线 $B C$ 作轴对称，点 $A$ 的对称点为点 $D$ ，连结 $B D$ ，作 $A P ⊥ B D$ ，垂足为 $P .$ 当 $△ A B C$ 是“ $[5 ， 3]$ 型三角形”时，求线段 $D P$ 的长.

查看试题解析
7. 定义：若连结三角形一个顶点和对边上一点的线段能把该三角形分成一个等腰三角形和一个直角三角形，我们称这条线段为该三角形的智慧线，这个三角形叫做智慧三角形.

(1)、如图1，在智慧三角形ABC中，AD⊥BC，AD为该三角形的智慧线，CD＝1，AC＝2，则BD长为， ∠B的度数为.

(2)、如图2，△ABC为等腰直角三角形，∠BAC＝90°，F是斜边BC延长线上一点，连结AF，以AF为直角边作等腰直角三角形AFE（点A，F，E按顺时针排列），∠EAF＝90°，AE交BC于点D，连结EC，EB.当∠BDE＝2∠BCE时，求证：ED是△EBC的智慧线.

(3)、如图3，△ABC中，AB＝AC＝5，BC²＝80.若△BCD是智慧三角形，且AC为智慧线，求△BCD的面积.

查看试题解析
8. 如果一个三角形能被一条线段分割成两个等腰三角形，那么称这条线段为这个三角形的特异线，称这个三角形为特异三角形．

(1)、如图1， $R t △ A B C$ 中，∠C=90°，CD=BD，求证：CD是 $R t △ A B C$ 的一条特异线；

(2)、如图2， $△ A B C$ 是一个等腰锐角三角形， $A B = A C$ ，且它是特异三角形，请求出∠A的度数．

查看试题解析
9. 如果三角形有一边上的中线恰好等于这边的长，那么我们称这个三角形为“奇妙三角形”．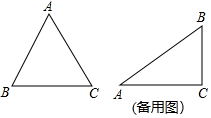

(1)、如图，在△ABC中，AB＝AC＝ $2 \sqrt{5}$ ， BC＝4，求证：△ABC是“奇妙三角形”；

(2)、在Rt△ABC中，∠C＝90°，AC＝ $2 \sqrt{3}$ ，若△ABC是“奇妙三角形”，求BC的长．

查看试题解析
10. 定义：两边的平方和与这两边乘积的差等于第三边平方的三角形叫做“和谐三角形”．如图1，在△ABC中，若AB²+AC²-AB⋅AC=BC² ，则△ABC是“和谐三角形”．

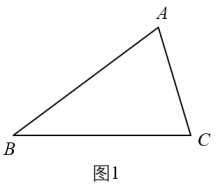(1)、等边三角形一定是“和谐三角形”，是命题（填“真”或“假”）．

(2)、若Rt△ABC中，∠C=90°，AB=c，AC=b，BC=a，且b>a，若△ABC 是“和谐三角形”，求a：b：c．

查看试题解析
11. 我们新定义一种三角形：若一个三角形中存在两边的平方差等于第三边上高的平方，则称这个三角形为勾股高三角形，两边交点为勾股顶点.

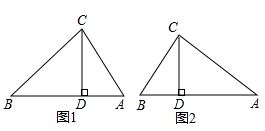(1)、特例感知
①等腰直角三角形勾股高三角形（请填写“是”或者“不是”）；

②如图1，已知△ABC为勾股高三角形，其中C为勾股顶点，CD是AB边上的高.若BD=2，AD=1，试求线段CD的长度.

(2)、深入探究
如图2，已知△ABC为勾股高三角形，其中C为勾股顶点且CA>CB，CD是AB边上的高.试探究线段AD与CB的数量关系，并给予证明.

查看试题解析
12. 引入概念1：如果一个三角形的三个角分别等于另一个三角形的三个角，那么称这两个三角形互为“等角三角形”．
引入概念2：从不等边三角形一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形．若分成的两个小三角形中一个是满足有两个角相等的三角形，另一个与原来三角形是“等角三角形”，我们把这条线段叫做这个三角形的“等角分割线”．

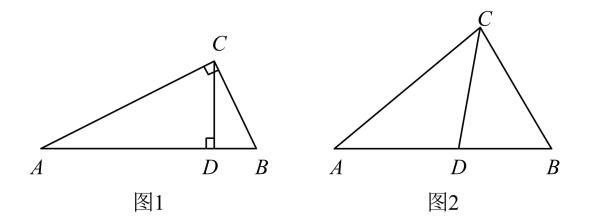
(1)、【理解概念】：
如图1，在Rt△ABC中，∠ACB＝90°，CD⊥AB ，请写出图中两对“等角三角形”．
① ．；②．．

(2)、如图2，在△ABC中，CD为角平分线，∠A＝40°，∠B＝60°．请你说明CD是△ABC的等角分割线．

(3)、【应用概念】：
在△ABC中，若∠A＝40°，CD为△ABC的等角分割线，请你直接写出所有可能的∠B度数．

查看试题解析
13. 当三角形中一个内角β是另外一个内角a的 $0.5$ 时，我们称此三角形为“友好三角形”．如果一个“友好三角形”中有一个内角为 $54 °$ ，那么这个“友好三角形”的“友好角a”的度数为．

查看试题解析
14. 定义：若一个三角形存在两边平方和等于第三边平方的3倍，则称此三角形为“平方倍三角形”．

(1)、若一个三角形的三边长分别是4， $\sqrt{11}$ 和3，这个三角形是否为平方倍三角形？请你作出判断并说明理由；

(2)、若一个直角三角形是平方倍三角形，求该直角三角形的三边之比（结果按从小到大的顺序排列）；

(3)、如图， $Rt △ A B C$ 中， $∠ A C B = 90 °$ ， $B C = 4$ ， $C D$ 为 $△ A B C$ 的中线，若 $△ B C D$ 是平方倍三角形，求 $△ A B C$ 的面积．

查看试题解析

二、一元一次不等式

15. 定义新运算“⊕”如下：当a＞b时，a⊕b＝ab+b；当a＜b时，a⊕b＝ab-b，若3⊕（x+2）＞0，则x的取值范围是（）

A、-1＜x＜1或x＜-2 B、x＜-2或1＜x＜2 C、-2＜x＜1或x＞1 D、x＜-2或x＞2

查看试题解析
16. 对于实数x，y，我们定义符号min{x，y}的意义为：当x＜y时，min{x，y}＝x；当x≥y时，min{x，y}＝y，如：min{6，﹣4}＝﹣4，min{4，4}＝4，min{ $\frac{3 x - 1}{2}$ ， $\frac{x + 1}{3}$ } $= \frac{x + 1}{3}$ 时，则x的取值范围为．

查看试题解析
17. 我们用[a]表示不大于a的最大整数，例如：[2.5]＝2，[3]＝3，[-2.5]＝-3；用＜a＞表示大于a的最小整数，例如：＜2.5＞＝3，＜3＞＝4，＜-2.5＞＝-2．根据上述规定，解决下列问题：

(1)、[-4.5]＝，＜3.01＞＝；

(2)、若x为整数，且[x]+＜x＞＝2023，求x的值；

(3)、若x、y满足方程组 ${\begin{array}{l} 3 [x] + 2 < y > = 3 \\ 3 [x] - < y > = - 6 \end{array}$ ，求x、y的取值范围．

查看试题解析
18. 新定义：若一元一次方程的解在一元一次不等式组解集范围内，则称该一元一次方程为该不等式组的“关联方程”，例如：方程 $x - 1 = 3$ 的解为 $x = 4$ ，而不等式组 ${\begin{array}{l} x - 1 > 1 \\ x - 2 < 3 \end{array}$ 的解集为 $2 < x < 5$ ，不难发现 $x = 4$ 在 $2 < x < 5$ 的范围内，所以方程 $x - 1 = 3$ 是不等式组 ${\begin{array}{l} x - 1 > 1 \\ x - 2 < 3 \end{array}$ 的“关联方程”．

(1)、在方程① $2 (x + 1) - x = - 3$ ；② $\frac{x + 1}{3} - 1 = x$ ；③ $2 x - 7 = 0$ 中，不等式组 ${\begin{array}{l} 2 x + 1 > x - 3 \\ 3 (x - 2) - x \leq 2 \end{array}$ 的“关联方程”是；（填序号）

(2)、关于x的方程 $2 x - k = 6$ 是不等式组 ${\begin{array}{l} \frac{x - 3}{2} \geq x \\ \frac{2 x + 5}{2} > \frac{1}{2} x \end{array}$ 的“关联方程”，求k的取值范围；

(3)、若关于x的方程 $\frac{x + 5}{2} - 3 m = 0$ 是关于x的不等式组 ${\begin{array}{l} \frac{x + 2 m}{2} > m \\ x - m \leq 2 m + 1 \end{array}$ 的“关联方程”，且此时不等式组有3个整数解，试求m的取值范围．

查看试题解析
19. 在平面直角坐标系中，对于点 $P (x ， y)$ ，若点 $Q$ 的坐标为 $(a y + x ， a x + y)$ ，其中 $a$ 为常数，对称点 $Q$ 是点 $P$ 的“ $a$ 级关联点”，例如：点 $P (1 ， 4)$ 的“2级关联点” $Q (2 \times 4 + 1 ， 1 \times 2 + 4)$ ，即 $Q (9 ， 6)$ .

(1)、已知点 $A (2 ， - 1)$ 的：“3级关联点”为 $B$ ，求点 $B$ 的坐标；

(2)、已知点 $P (x ， y)$ 关于“2级关联点”为 $(0 ， 3)$ ，求 $P$ 的坐标；

(3)、点 $(2 m ， m - 1)$ 关于-4级关联点在第三象限，求 $m$ 的范围。

查看试题解析
20. 阅读以下材料：对于三个数a ， b ， c ，用M{a ， b ， c}表示这三个数的平均数，用min{a、b ， c}表示这三个数中最小的数．例如：M{﹣1，2，3}＝ $\frac{- 1 + 2 + 3}{3} = \frac{4}{3}$ ， min{-1，2，3}＝﹣1；min{﹣1，2，a}＝ ${\begin{cases} a (a \leq - 1) \\ - 1 (a > - 1) \end{cases}$ 解决下列问题：

(1)、min{ $\frac{1}{2}$ ， $\frac{\sqrt{2}}{2}$ ， $\frac{\sqrt{3}}{2}$ }＝，若min{2，2x+2，4﹣2x}＝2，则x的范围为；

(2)、①如果M{2，x+1，2x}＝min{2，x+1，2x}，求x；
②根据①，你发现了结论“如果M{a ， b ， c}＝min{a ， b ， c}，那么（填a ， b ， c的大小关系）”．证明你发现的结论；
③运用②的结论，填空：若M{2x+y+2，x+2y ， 2x﹣y}＝min{2x+y+2，x+2y，2x﹣y}，则x+y＝．

查看试题解析