《特殊三角形》精选压轴题—2024年浙教版数学八（上）期中复习
试卷更新日期：2024-10-19 类型：复习试卷
一、选择题
-
1. 如图，△AOB≌△ADC，点B和点C是对应顶点，∠O=∠D=90°，记∠OAD=α，∠ABO=β，当BC∥OA时，α与β之间的数量关系为（ ）.
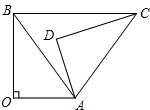A、α＝β B、α＝2β C、α+β＝90° D、α+2β＝180°2. 如图，在等腰Rt△ABC中，∠C＝90°，AC＝6，F是AB边上的中点，点D，E分别在AC，BC边上运动，且保持AD＝CE，连接DE，DF，EF.在此运动变化的过程中，下列结论：①△DFE是等腰直角三角形；②四边形CDFE的面积是定值9；③△DFE的面积最小值为4.5；④DE长度的最小值为3.其中正确的结论是（ ）
A、①②③ B、①②④ C、①③④ D、②③④3. 如图，BD是△ABC的角平分线，BA＝BC＝10，AC＝12，DE∥BC ， P ， Q分别是BD和BC上的任意一点；连接PA ， PC ， PQ ， AQ ， 给出下列结论：①PC+PQ≥AQ；②AE+DE＝BC；③PC+PQ的最小值是；④若PA平分∠BAC ， 则△APD的面积为9．其中正确的是（ ）
A、①②③ B、①②④ C、①③④ D、②③④4. 如图，已知等边△ABC的边长为4，点P是边BC上一点，BP＝1，则AP＝ ， 若点Q是边AC上一点，BQ＝AP ， 则AQ＝ ．
5. 如图，在Rt△ABC中，∠ACB=90°，分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BDMC，记四块阴影部分的面积分别为、、、.若已知 ， 则下列结论：①；②；③；④ ，其中正确的结论是（ ）
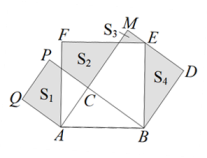A、①②③ B、①②④ C、①③④ D、②③④6. 如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O ， 过O点作EF∥BC交AB于点E ， 交AC于点F ， 过点O作OD⊥AC于D ， 下列四个结论．①EF＝BE+CF；②∠BOC＝90°+∠A；③点O到△ABC各边的距离相等；④设OD＝m ， AE+AF＝n ， 则S△AEF＝mn ， 正确的结论有（ ）个．
A、1个 B、2个 C、3个 D、4个7. 如图，Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，将边AC沿CE翻折，使点A落在AB上的点D处；再将边BC沿CF翻折，使点B落在CD的延长线上的点B′处，两条折痕与斜边AB分别交于点E、F ， 则的面积为（ ）
A、 B、 C、 D、8. 如图，等腰Rt△ABC中，∠BAC=90°，AD⊥BC于D，∠ABC的平分线分别交AC、AD于E、F两点，M为EF的中点，延长AM交BC于点N，连接DM、MC下列结论：①DF=DN；②ABE≌△MBN；③△CMN是等腰三角形；④AE=CN；，其中正确的结论个数是（ ）
A、1个 B、2个 C、3个 D、4个二、填空题
-
9. 如图，在△ABC中，AC＝BC，∠ACB＝90°，直角∠EDF的顶点D是AB的中点，两边DE，DF分别交AC，BC于点E，F，有以下结论：①CE＝BF：②△EDF是等腰直角三角形；③EF＝CD：④S四边形CFDE＝S△ABC ． 上述结论中一定正确的是（填上正确的序号）
10. 如图，在边长为2的等边三角形中，点D，E分别是BC，AB的中点，点P是AD上一动点，则△PBE的周长最小值为.
11. 如图，在等腰中， ， 点M，N分别是边 ， 上的动点，与关于直线对称，点B的对称点为 ． 当且时，若 ， 则的面积为.
12. 如图，△ABC和△AEF都是等腰直角三角形，∠BAC＝∠EAF＝90°，BC＝4， ， 点E在射线BD上运动，连结BF，则在点E运动的过程中，线段BF的最小值是 ．
13. 如图，折叠等腰三角形纸片ABC ， 使点C落在边AB上的点F处，折痕为DE ． 已知AB＝AC ， FD⊥BC ．
(1)、∠AFE＝度；(2)、如果AF＝3，BF＝5，则CE＝ ．三、解答题
-
14. 如图，已知△ABC中，∠B＝90°，AB＝8cm，BC＝6cm，P、Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒.
(1)、出发2秒后，求PQ的长(2)、从出发几秒钟后，△PQB第一次能形成等腰三角形？(3)、当点Q在边CA上运动时，求能使△BCQ成为等腰三角形的运动时间.15. 我们新定义一种三角形：若一个三角形中存在两边的平方差等于第三边上高的平方，则称这个三角形为勾股高三角形，两边交点为勾股顶点.
(1)、特例感知等腰直角三角形勾股高三角形(填“是”或“不是”)；
(2)、如图①，为勾股高三角形，其中为勾股顶点，是边上的高.若 ， 试求线段的长度.(3)、深入探究如图②，为勾股高三角形，其中为勾股顶点且 ， 是边上的高.试探究线段与的数量关系，并给予证明.
(4)、推广应用如图③，等腰三角形为勾股高三角形，其中 ， 为边上的高，过点向边引平行线与边交于点.若 ， 试求线段的长度.
16. 如图，在Rt△ABC中，∠ABC＝90°，AB＝4，BC＝3，点D为AC边上的动点，点D从点C出发，沿边CA往A运动，当运动到点A时停止，若设点D运动的时间为t秒，点D运动的速度为每秒1个单位长度．
(1)、当t＝2时，分别求CD和AD的长；(2)、当t为何值时，△CBD是直角三角形？(3)、若△CBD是等腰三角形，请求出t的值．17. 定义：若以三条线段 ， ， 为边能构成一个直角三角形，则称线段 ， ， 是勾股线段组.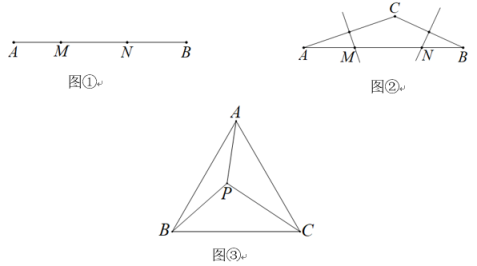
(1)、如图①，已知点M，N是线段AB上的点，线段AM，MN，NB是勾股线段组.若AB=12，AM=3，求MN的长；(2)、如图②，△ABC中，∠A=17°，∠B=28°，边AC，BC的垂直平分线分别交AB于点M，N，求证：线段AM，MN，NB是勾股线段组；(3)、如图③，在等边△ABC，P为△ABC内一点，线段AP，BP，CP构成勾股线段组，CP为此线段组的最长线段，求∠APB的度数.18.
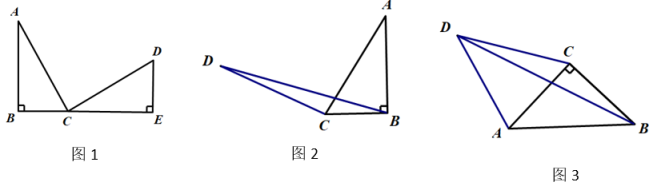(1)、【问题发现】如图1，在△ABC与△CDE中，∠B=∠E=∠ACD＝90°，AC＝CD，B、C、E三点在同一直线上，AB＝4，ED＝3，则BE=.
(2)、【问题提出】如图2，在Rt△ABC中，∠ABC＝90°，BC＝3，过点C作CD⊥AC，且CD＝AC，求△BCD的面积.
(3)、【问题解决】如图3，四边形ABCD中，∠ABC=∠CAB=∠ADC＝45°，△ACD面积为14且CD的长为7，求△BCD的面积.
19. 如图1，直线AM⊥AN ， AB平分∠MAN ， 过点B作BC⊥BA交AN于点C；动点E、D同时从A点出发，其中动点E以2cm/s的速度沿射线AN方向运动，动点D的运动速度为1cm/s；已知AC＝6cm ， 设动点D ， E的运动时间为t ．
(1)、试求AB的长；(2)、当点D在射线AM上运动时，满足S△ADB：S△BEC＝3：4，试求点D ， E的运动时间t的值；(3)、当动点D在直线AM上运动，点E在射线AN上运动时，是否存在某个时间t ， 使得△ADB与△BEC全等？若存在，请求出时间t的值；若不存在，请说出理由．20. 如图，在Rt△ABC中， ， 点P为边上的一点，将线段绕点A顺时针方向旋转（点P对应点）．当旋转至时，点恰好在同一直线上，此时作于点E．
(1)、求证：∠CBP＝∠ABP；(2)、若AB-BC=4，AC=8，求△PBC的面积；(3)、在（2）的条件下，点N为边上一动点，点M为边上一个动点，连接 ， 求的最小值，请直接写出答案.21. 如图，△ABC中，BA＝BC，CO⊥AB于点O，AO＝4，BO＝6．
(1)、求BC，AC的长；(2)、若点D是射线OB上的一个动点，作DE⊥AC于点E，连结OE．①当点D在线段OB上时，若△AOE是以AO为腰的等腰三角形，请求出所有符合条件的OD的长．
②设DE交直线BC于点F，连结OF，若S△OBF：S△OCF＝1：4，则BD的长为 ▲（直接写出所有结果）．