精选实践探究题—2024年浙教版数学九（上）期中复习

试卷更新日期：2024-10-19 类型：复习试卷

进入出卷网下载

一、二次函数

1.

(1)、【问题初探】
综合与实践数学活动课上，张老师给出了一个问题：
已知二次函数y＝x²+2x－3，当－2≤x≤2时，y的取值范围为；
①小伟同学经过分析后，将原二次函数配方成y＝a(x－h)²+k
形式，确定抛物线对称轴为直线x＝h ，通过－2、h和2的大小
关系，分别确定了最大值和最小值，进而求出y的取值范围；
②小军同学画出如图的函数图象，通过观察图象确定了y的取值范围；请你根据上述两名同学的分析写出y的取值范围是；

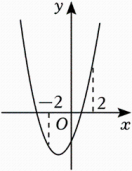(2)、【类比分析】
张老师发现两名同学分别从“数”和“形”的角度分析、解决问题，为了让同学们更好感悟“数形结合”思想，张老师将前面问题变式为下面问题，请你解答：已知二次函数y＝－x²+2x－3，当－2≤x≤2时，求y的取值范围；

(3)、【学以致用】
已知二次函数y＝－x²+6x－5，当a≤x≤a+3时，二次函数的最大值为y₁ ，最小值为y₂ ，若y₁－y₂＝3，求a的值．

查看试题解析

2. 根据以下素材，探索完成任务．

绿化带灌溉车的操作方案

素材1	辆绿化带灌溉车正在作业，水从喷水口喷出，水流的上下两边缘可以抽象为两条抛物线的一部分：喷水口离开地面高1.6米，上边缘抛物线最高点离喷水口的水平距离为3米，高出\|喷水口0.9米，下边缘水流形状与上边缘相同，且喷水口是最高点。
素材2	路边的绿化带宽4米
素材3	绿化带正中间种植了行道树，为了防治病虫害、增加行道树的成活率，园林工人给树木“打针”。针一般打在离地面1.5米到2米的高度(包含端点)。

问题解决

(1)、任务1：确定上边缘水流形状

建立如图所示直角坐标系，求上边缘抛物线的函数表达式．

(2)、任务2：探究灌溉范围

灌溉车行驶过程中喷出的水能浇浓到整个绿化带吗？请说明理由．

(3)、任务3：拟定设计方案

灌溉时，发现水流的上下两边缘冲击力最强，喷到针筒容易造成针筒脱落。那么请问在满足最大灌溉面积的前提下对行道树“打针”是否有影响，并说明理由；若你认为有影响，请给出具体的“打针”范围。

查看试题解析

3. 根据以下素材，探索完成任务，
素材1  图1是中国传统建筑——凉亭，其截面为两个成轴对称的抛物线的一部分（如图2）．凉亭外延水平宽度EC为6米，亭高AO＝4米，在抛物线最低处由一根高为3.1米的柱子支撑，柱子离亭正中心O点距离为2.4米；
素材2  为了美观，拟在凉亭右侧抛物线内悬挂一盏上下长度为0.5米，左右宽度为0.2米的灯笼（如图3），要使得整个灯笼处于右侧且保持离地至少3米的安全距离（灯笼挂钩G位于其中间最上端）.

(1)、任务1  确定凉亭右侧形状：在图2中建立合适的直角坐标系，求凉亭右侧抛物线的函数表达式；

(2)、任务2  探究悬挂位置：在你建立的坐标系中，在安全的前提下，确定灯笼的悬挂水平位置范围.

查看试题解析
4. 根据以下素材，探索完成任务．
素材1  图1为某公园的抛物线型拱桥，图2是其横截面示意图，测得水面宽度 $A B = 24$ 米，拱顶离水面的距离为 $C D = 4$ 米．
素材2  拟在公园里投放游船供游客乘坐，载重最少时，游船的横截面如图3所示，漏出水面的船身为矩形，船顶为等腰三角形．测得相关数据如下： $E F = E K = 1.7$ 米， $F K = 3$ 米， $G H = I J = 1.26$ 米， $F G = J K = 0.4$ 米．
素材3  为确保安全，拟在石拱桥下面的P，Q两处设置航行警戒线，要求如下：
①游船底部 $H I$ 在P，Q之间通行；
②当载重最少通过时，游船顶部E与拱桥的竖直距离至少为 $0.5$ 米．

(1)、任务1  确定拱桥形状：在图2中建立合适的直角坐标系，并求这条抛物线的函数表达式．

(2)、任务2  设计警戒线之间的宽度：求 $P Q$ 的最大值.

查看试题解析

5. 根据以下素材，探索完成任务

确定文具套餐售价
素材1	某书店销售一款文具套装，当每套文具售价为30元时，月销售量为200套，经市场调查表明，每套文具售价每降价1元，则月销售量增加20套．设每套文具的售价为x元（x为正整数），月销售量为y套．
素材2	该文具套装的成本是10元/套．
素材3	为促进公益，在售价不低于进价且每套文具获利不高于95%的前提下，该书店决定，每月捐赠400元给慈善机构．

问题解决：

(1)、任务1：分析变量分析

求y关于x的函数表达式．

(2)、任务2：计算月利润

当售价为多少时，月利润W获得最大？最大利润是多少？

(3)、任务3：确定合理售价

为了保证捐款后月利润不低于3040元，文具套装的售价可以取哪些数值．

查看试题解析

6. 《函数的图象与性质》拓展学习片段展示：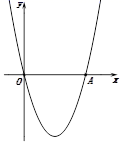

(1)、（问题）
如图①，在平面直角坐标系中，抛物线y=a（x-2）²-4经过原点O，与x轴的另一个交点为A，则a= ，点A的坐标为 .

(2)、（操作）
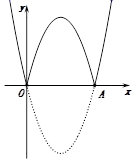
将图①中的抛物线在x轴下方的部分沿x轴翻折到x轴上方，如图②.直接写出翻折后的这部分抛物线对应的函数解析式：.

(3)、（探究）
在图②中，翻折后的这部分图象与原抛物线剩余部分的图象组成了一个“W”形状的新图象，则新图象对应的函数y随x的增大而增大时，x的取值范围是.

(4)、（应用）结合上面的操作与探究，继续思考：如图③，若抛物线y=（x-h）²-4与x轴交于A，B两点（A在B左），将抛物线在x轴下方的部分沿x轴翻折，同样，也得到了一个“W”形状的新图象.
求A、B两点的坐标；（用含h的式子表示）

(5)、当1＜x＜2时，若新图象的函数值y随x的增大而增大，求h的取值范围.

查看试题解析

7. 根据以下素材，探索完成任务．

如何设计喷泉喷头的升降方案？

素材1

如图，有一个可垂直升降的喷泉，喷出的水柱呈抛物线．记水柱上某一点到喷头的水平距离为x米，到湖面的垂直高度为y米．当喷头位于起始位置时，测量得x与y的四组数据如下：

x（米）	0	2	3	4
y（米）	1	2	1.75	1

素材2

公园想设立新的游玩项目，通过升降喷头，使游船能从水柱下方通过，如图，为避免游船被喷泉淋到，要求游船从水柱下方中间通过时，顶棚上任意一点到水柱的竖直距离均不小于0.4米．已知游船顶棚宽度为2.8米，顶棚到湖面的高度为2米．

问题解决

任务1

确定喷泉形状

结合素材1，求y关于x的表达式．

任务2

探究喷头升降方案

为使游船按素材2要求顺利通过，求喷头距离湖面高度的最小值．

查看试题解析

8. 根据以下素材，探索完成任务．

如何设计喷水装置的高度？
素材1	如图1为某公园的圆形喷水池，图2是其示意图，O为水池中心，喷头A、B之间的距离为20米，喷射水柱呈抛物线形，水柱距水池中心 $7 m$ 处达到最高，高度为 $5 m$ ．水池中心处有一个圆柱形蓄水池，其中高 $C F$ 为 $1.8$ 米．
素材1
素材2	如图3，拟在圆柱形蓄水池中心处建一喷水装置 $O P (O P ⊥ C D)$ ，从点P向四周喷射抛物线形水柱且满足以下条件： ①不能碰到图2中的水柱； ②落水点G，M的间距为 $G M = 0.4 m$ ； ③水柱的最高点与点P的高度差为 $0.8 m$ ； ④从点P向四周喷射与图2中形状相同的抛物线形水柱．
问题解决
任务1	确定水柱形状	在图2中以点O为坐标原点，水平方向为x轴建立直角坐标系，并求这条抛物线的函数表达式．
任务2	探究落水点位置	在建立的坐标系中，求落水点G的坐标．
任务3	拟定喷水装置的高度	求出喷水装置 $O P$ 的高度．

查看试题解析

某饭店特制了一批高脚杯，分为男士杯和女士杯（如图1），相关信息如下：

素材	内容
素材1	高脚杯：如图1，类似这种杯托上立着一只细长脚的杯子．从下往上分为三部分：杯托，杯脚，杯体．杯托为一个圆；水平放置时候，杯脚经过杯托圆心，并垂直任意直径；杯体的水平横截面都为圆，这些圆的圆心都在杯脚所在直线上．
素材2	图2坐标系中，特制男士杯可以看作线段AB ， OC ，抛物线DCE（实线部分），线段DF ，线段EG绕y轴旋转形成的立体图形（不考虑杯子厚度，下同）．图2坐标系中，特制女士杯可以看作线段AB ， OC ，抛物线FCG（虚线部分）绕y轴旋转形成的立体图形．
素材3	已知，图2坐标系中，OC＝50mm ，记为C（0，50），D（﹣25，75），E（25，75），F（﹣25，150），G（25，150）．

根据以上素材内容，尝试求解以下问题：

(1)、求抛物线DCE和抛物线FCG的解析式；

(2)、当杯子水平放置及杯内液体（无泡沫）静止时，若男士杯中液体与女士杯中液体最深处深度均为30mm ，求两者液体最上层表面圆面积相差多少？（结果保留π）

(3)、当杯子水平放置及杯内液体（无泡沫）静止时，若男士杯中液体与女士杯中液体最深处深度相等，两者液体最上层表面圆面积相差450πmm² ，求杯中液体最深度为多少？

查看试题解析

10. 根据以下信息，探索完成任务．

如何设计种植方案？

素材1

某校为响应国家政策，在校内100平方米的土地上进行种植课实践，现有A、B，C三种作物的相关信息如表所示．已知5株A作物和2株B作物的产量共为7千克：10株A作物和6株B作物的产量共为15千克．

	A作物	B作物	C作物
每平方米种植株树（株)	2	10	4
单株产量（千克）	x	y	1.6

素材2

由于A作物植株间距较大，可增加A作物每平方米的种植株树．经过实验发现，每平方米种植A作物每增加1株，A作物的单株产量减少0.1千克．而B，C单株产量不发生变化．

素材3

若同时种植A，B，C三种作物，实行分区域种植．

问题解决

任务1

确定单株产量

求x，y的值．

单一种植（全部种植A作物）

任务2

预估种植策略

要使A作物每平方米产量为4千克，则每平方米应种植多少株？

分区种植（种植A，B，C三种作物）

任务3

规划种植方案

设这100平方米的土地中有a平方米用于种植A作物，且每平方米的产量最大：有b平方米用于种植B作物，剩余的全用来种植C作物，a，b均为正整数．当这100平方米总产量为577千克时，求这三种作物的种植方案．

查看试题解析

11. 综合与实践
问题提出：某兴趣小组开展综合实践活动：在 $R t △ A B C$ 中， $∠ C = 90 °$ ， D为 $A C$ 上一点， $C D = \sqrt{2}$ ，动点P以每秒1个单位的速度从C点出发，在三角形边上沿 $C \to B \to A$ 匀速运动，到达点A时停止，以 $D P$ 为边作正方形 $D P E F$ 设点P的运动时间为 $t s$ ，正方形 $D P E F$ 的面积为S ，探究S与t的关系.

(1)、初步感知：如图1，当点P由点C运动到点B时，
①当 $t = 1$ 时， $S =$ ．
②S关于t的函数解析式为．

(2)、当点P由点B运动到点A时，经探究发现S是关于t的二次函数，并绘制成如图2所示的图象请根据图象信息，求S关于t的函数解析式及线段 $A B$ 的长．

(3)、延伸探究：若存在3个时刻 $t_{1} ， t_{2} ， t_{3}$ （ $t_{1} < t_{2} < t_{3}$ ）对应的正方形 $D P E F$ 的面积均相等．
① $t_{1} + t_{2} =$ ▲ ；
②当 $t_{3} = 4 t_{1}$ 时，求正方形 $D P E F$ 的面积．

查看试题解析

12. 完成项目化学习：《蔬菜大棚的设计》．

《蔬菜大棚的设计》
驱动问题	1、如何利用函数模型，刻画蔬菜大棚的棚面？ 2、如何安装排气装置，保证蔬菜大棚的通风性？ 3、如何设计大棚间距，保障蔬菜大棚的采光性？
项目背景	蔬菜大棚是一种具有出色的保温性能的框架覆膜结构，它出现使得人们可以吃到反季节蔬菜．如图，一般蔬菜大棚使用竹结构或者钢结构的骨架，这样就形成了一个温室空间．
数学建模	如图，某个温室大棚的横截面可以看作矩形ABCD和抛物线AED构成，其中AB＝3m，取BC中点O，过点O作线段BC的垂直平分线OE交抛物线AED于点E，BC所在直线为x轴，OE为y轴建立如图所示平面直角坐标系．抛物线AED的顶点E（0，4）
问题解决	如图，为了保证该蔬菜大棚的通风性，该大棚要安装两个正方形孔的排气装置LFGT，若FL＝NR＝0.75m，求两个正方形装置的间距GM的长．
问题解决	为了保证两个蔬菜大棚间的采光不受影响，如图，在某一时刻，此时大棚截面的阴影为CK，求CK的长．

查看试题解析

13. 根据素材回答问题：

素材1	如图1，空地上有两条互相垂直的小路OP，OQ，中间有一正方形ABCD水池，已知水池的边长为4 米，AB//OQ，AD//OP，且AB与OQ的距离为10 米，AD与OP的距离为8 米．
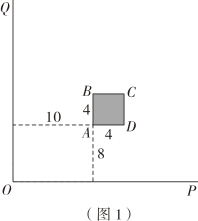
素材2	现利用两条小路，再购置30 米长的栅栏(图中的细实线）在空地上围出一个花圃，要求围起来的栅栏与小路相互平行（或垂直），靠小路和水池的都不需要栅栏，接口损耗忽略不计．
	任务1	任务2
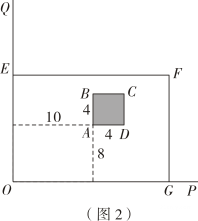
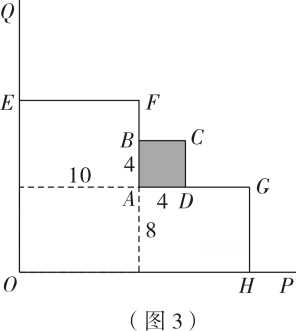
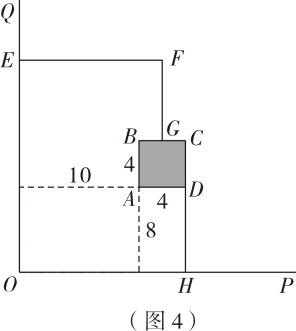
	小明同学按如图2的设计，若EF=16米，求出花圃的面积（不包含水池的面积）．	若按如图3、如图4设计方案，通过计算说明哪种方案的最大面积更大．
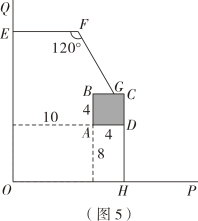
项目反思	如果栅栏不一定与墙面垂直（或平行），你还能设计出比以上方案面积更大的花圃吗？某学习小组在探究的过程中，设计了方案如图5，你认为图5的最大面积与以上方案比较，哪个更大，请通过计算说明．

查看试题解析

二、圆

14. 根据背景素材，探索解决问题．

测算石拱桥拱圈的半径
素材1	某数学兴趣小组测算一座石拱桥拱圈的半径（如图1），石拱桥由矩形的花岗岩叠砌而成，上、下的花岗岩错缝连接（花岗岩的各个顶点落在上、下花岗岩各边的中点，如图2所示）．
素材2	通过观察发现A，B，C三个点都在拱圈上，A是拱圈的最高点，且在两块花岗岩的连接处，B，C两个点都是花岗岩的顶点（如图3）．
素材3	如果没有带测量工具，那么可以用身体的“尺子”来测，比如前臂长（包括手掌、手指）（如图4），利用该方法测得一块花岗岩的长和宽（如图5）．
问题解决
任务1	获取数据	通过观察、计算B，C两点之间的水平距离及铅垂距离（高度差）．
任务2	分析计算	通过观察、计算石拱桥拱圈的半径．

注：测量、计算时，都以“肘”为单位．

查看试题解析

15. 根据素材解决问题．

设计货船通过圆形拱桥的方案
素材1	图1中有一座圆拱石桥，图2是其圆形桥拱的示意图，测得水面宽AB=16m，拱顶离水面的距离CD=4m．
素材2	如图3，一艘货船露出水面部分的横截面为矩形EFGH，测得EF=3m，EH=10m．因水深足够，货船可以根据需要运载货物．据调查，船身下降的高度y(米)与货船增加的载重量x (吨)满足函数关系式y= $\frac{1}{100}$ x．
问题解决
任务1	确定桥拱半径	求圆形桥拱的半径．
任务2	拟定设计方案	根据图3状态，货船能否通过圆形桥拱？若能，最多还能卸载多少吨货物？若不能，至少要增加多少吨货物才能通过？

查看试题解析

16. 请阅读下列材料，并完成相应的任务：阿基米德折弦定理，阿基米德（公元前287年一公元前212年），伟大的古希腊哲学家、百科式科学家、数学家、物理学家、力学家，静态力学和流体静力学的奠基人，并且享有“力学之父”的美称，阿基米德和高斯，牛顿并列为世界三大数学家．
阿拉伯Al-Binmi（973年一1050年）的译文中保存了阿基米德折弦定理的内容，苏联在1964年根据Al-Binmi译本出版了俄文版《阿基米德全集》，第一题就是阿基米德折弦定理．
阿基米德折弦定理：如图1，AB和BC是⊙O的两条弦（即折线ABC是圆的一条折弦），BC＞AB，M是 $\overset{⌢}{A B C}$ 的中点，则从M向BC所作垂线的垂足D是折弦ABC的中点，即CD＝AB+BD．
小明同学运用“截长法”和三角形全等来证明CD＝AB+BD，过程如下：
证明：如图2所示，在CB上截取CG＝AB，连接MA，MB，MC和MG．
∵M是 $\overset{⌢}{A B C}$ 的中点，∴MA＝MC，…

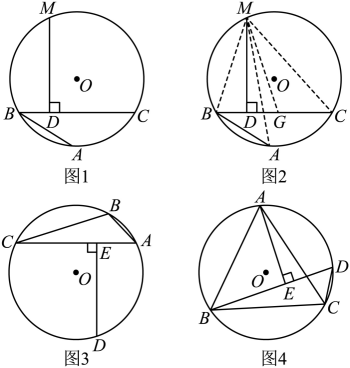(1)、请按照上述思路，写出该证明的剩余部分；

(2)、如图3，在⊙O中，BD =CD，DE⊥AC，若AB = 4，AC = 10，则AE的长度为；

(3)、如图4，已知等边 $△$ ABC内接于⊙O，AB = 8，D为 $\overset{⌢}{A C}$ 上一点，∠ABD = 45°，AE⊥BD于点E，求 $△$ BDC的周长．

查看试题解析

三、相似

17.

(1)、【基础巩固】
如图1，在 $△ A B C$ 中，D ， E分别在 $A B$ ， $A C$ 上，连结DE，若 $∠ A D E = ∠ C$ ，求证： $A D \cdot A B = A E \cdot A C$ .

(2)、【尝试应用】
如图2，在 $△ A B C$ 中，在 $A C$ 上取一点E ，以 $A E$ 为一边构造平行四边形 $A D E F$ ，使点D ， F恰好落在 $A C$ ， $B C$ 上，连结 $D E$ ，若 $∠ D E F = ∠ C$ ， $A D = 4$ ， $B D = 2$ ，求 $A C$ 的长.

(3)、【拓展提高】
如图3，在 $△ A B C$ 中，在 $A C$ 上取一点E ，以 $A E$ 为一边构造平行四边形 $A D E F$ ，使点F恰好落在 $B C$ 上，连结 $D E$ ， $B D$ ，若 $∠ D E F = ∠ C$ ， $∠ E F C = ∠ A B D$ ， $A E = 4$ ， $C E = 2$ ，求 $A B$ 的长。

查看试题解析
18.

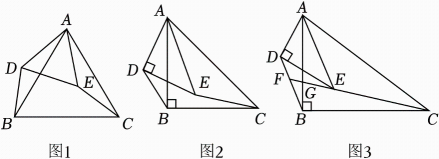(1)、【问题呈现】如图1，△ABC和△ADE都是等边三角形，连接BD，CE．求证：BD＝CE．

(2)、【类比探究】如图2，△ABC和△ADE都是等腰直角三角形，∠ABC＝∠ADE＝90°．连接BD，CE．则 $\frac{B D}{C E} =$ ．

(3)、【拓展提升】如图3，△ABC和△ADE都是直角三角形，∠ABC＝∠ADE＝90°，且 $\frac{A B}{B C} = \frac{A D}{D E} = \frac{3}{4}$ ．连接BD，CE．
①求 $\frac{B D}{C E}$ 的值；
②延长CE交BD于点F，交AB于点G．若 $\frac{B G}{C G} = \frac{1}{4}$ ， AB＝6，求BF的长．

查看试题解析
19. 在△ABC中，BD⊥AC于点D，点P为射线BD上任一点（点B除外），连接AP，将线段PA绕点P顺时针方向旋转α，α＝∠ABC，得到PE，连接CE.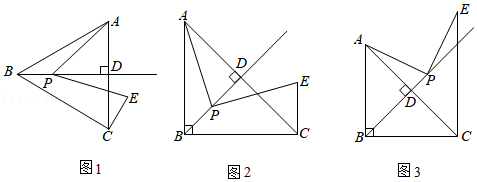

(1)、【观察发现】如图1，当BA＝BC，且∠ABC＝60°时，BP与CE的数量关系是， BC与CE的位置关系是 .

(2)、【猜想证明】如图2，当BA＝BC，且∠ABC＝90°时，（1）中的结论是否成立？若成立，请予以证明；若不成立，请说明理由.（请选择图2，图3中的一种情况予以证明或说理）

(3)、【拓展探究】在（2）的条件下，若AB＝8，AP＝5 $\sqrt{2}$ ，请直接写出CE的长.

查看试题解析
20.

(1)、【探究证明】某班数学课题学习小组对矩形内两条互相垂直的线段与矩形两邻边的数量关系进行探究，提出下列问题，请你给出证明：
如图①，在矩形 $A B C D$ 中， $E F ⊥ G H$ ， $E F$ 分别交 $A D 、 B C$ 于点E、F， $G H$ 分别交 $A B 、 D C$ 于点G、H，求证： $\frac{E F}{G H} = \frac{A B}{A D}$ ；

(2)、【结论应用】如图②，将矩形 $A B C D$ 沿 $E F$ 折叠，使得点B和点D重合，若 $A B = 4 ， B C = 6$ ，求折痕 $E F$ 的长；

(3)、【拓展运用】如图③，将矩形 $A B C D$ 沿 $E F$ 折叠．使得点D落在 $A B$ 边上的点G处，点C落在点P处，得到四边形 $E F P G$ ，若 $A B = 4 ， B C = 6 ， E F = \frac{4 \sqrt{10}}{3}$ ，求 $B P$ 的长．

查看试题解析
21.

(1)、【基础巩固】如图1，在 $△ A B C$ 中， $D ， E ， F$ 分别为 $A B ， A C ， B C$ 上的点， $D E ∥ B C ， A F$ 交 $D E$ 于点G，求证： $\frac{D G}{E G} = \frac{B F}{C F}$ .

(2)、【尝试应用】如图2，已知 $D 、 E$ 为 $△ A B C$ 的边 $B C$ 上的两点，且满足 $B D = 2 D E = 4 C E$ ，一条平行于 $A B$ 的直线分别交 $A D 、 A E$ 和 $A C$ 于点 $L 、 M$ 和 $N$ ，求 $\frac{L M}{M N}$ 的值.

(3)、【拓展提高】如图3，点E是正方形 $A B C D$ 的边 $C D$ 上的一个动点， $A B = 3$ ，延长 $C D$ 至点F，使 $D F = 2 D E$ ，连接 $C G$ ，求 $C G$ 的最小值.

查看试题解析
22. 如图：

(1)、【问题提出】
如图1，在正方形ABCD中，AC，BD是对角线，点 $E$ 在AB边上，点 $F$ 在对角线AC上， $∠ E D F = 4 5^{°}$ ，求证： $B E = \sqrt{2} C F$ .

(2)、【尝试应用】
如图2，在矩形ABCD中， $A B = 3 ， A D = 4$ ，点 $E$ 在AB边上，点 $F$ 在对角线AC上， $∠ E D F = ∠ A C D ， A E = 1$ ，求CF的长

(3)、【拓展提高】
如图3，在菱形ABCD中， $A B = 5 ， A C = 6$ ，点 $E$ 在AB边上，点 $F$ 在对角线AC上， $∠ E D F = \frac{1}{2} ∠ A D C ， C F = 1$ ，作 $B H ⊥ A D$ 交DA的延长线于点H，DE的延长线交BH于点 $P$ ，请直接写出BP，BE的长.

查看试题解析
23.

(1)、【基础巩固】如图1，在 $Δ A B C$ 中， $D$ ， $E$ ， $F$ 分别为 $A B$ ， $A C$ ， $B C$ 上的点， $D E / / B C$ ， $B F = C F$ ， $A F$ 交 $D E$ 于点 $G$ ，求证： $D G = E G$ ．

(2)、【尝试应用】如图2，在（1）的条件下，连结 $C D$ ， $C G$ ．若 $C G ⊥ D E$ ， $C D = 6$ ， $A E = 3$ ，求 $\frac{D E}{B C}$ 的值．

(3)、【拓展提高】如图3，在 $▱ A B C D$ 中， $∠ A D C = 45 °$ ， $A C$ 与 $B D$ 交于点 $O$ ， $E$ 为 $A O$ 上一点， $E G / / B D$ 交 $A D$ 于点 $G$ ， $E F ⊥ E G$ 交 $B C$ 于点 $F$ ．若 $∠ E G F = 40 °$ ， $F G$ 平分 $∠ E F C$ ， $F G = 10$ ，求 $B F$ 的长．

查看试题解析