精选新定义型题—2024年浙教版数学九（上）期中复习

试卷更新日期：2024-10-19 类型：复习试卷

进入出卷网下载

一、选择题

1. 定义：给定关于x的函数 y ，对于该函数图象上任意两点（x₁ ， y₁），（x₂ ， y₂），当x₁﹤x₂时，都有y₁﹤y₂ ，称该函数为增函数.根据以上定义，下列函数中①y=2x；② $y = - x + 1$ ；③ $y = x_{}^{2} (x > 0)$ ；④ $m x^{2} - (m - 1) x - 1 = 0$ ，是增函数的（）

A、①③④ B、①② C、③④ D、①③

查看试题解析
2. 黄金分割由于其美学性质，受到摄影爱好者和艺术家的喜爱，摄影中有一种拍摄手法叫黄金构图法．其原理是：如图，将正方形ABCD的底边BC取中点E ，以E为圆心，线段DE为半径作圆，其与底边BC的延长线交于点F ，这样就把正方形ABCD延伸为矩形ABFG ，称其为黄金矩形．若CF＝4a ，则AB＝（　　）

A、（ $\sqrt{5}$ ﹣1）a B、（2 $\sqrt{5}$ ﹣2）a C、（ $\sqrt{5}$ +1）a D、（2 $\sqrt{5}$ +2）a

查看试题解析
3. 定义平面内任意两点P(x₁ ， y₁)、Q(x₂ ， y₂)之间的距离d_PQ=|x₂-x₁|+|y₂-y₁|称为这两点间的曼哈顿距离(简称为曼距)．例如，在平面直角坐标系中，点P(-3，-2)与点Q(2，2)之间的曼距d_PQ=|-3-2|+|-2-2|=5+4=9，若点A在直线y= $\frac{1}{2}$ x-2上，点B为抛物线y=x²+2x上一点，则曼距d_AB的最小值（）

A、 $\frac{23 \sqrt{5}}{40}$ B、 $\frac{69}{40}$ C、 $\frac{23}{16}$ D、 $\frac{3}{2}$

查看试题解析
4. 定义：在平面直角坐标系中，若点 $A$ 满足横、纵坐标都为整数，则把点 $A$ 叫做整点．如： $B (3, 0)$ ， $C (- 1, 3)$ 都是整点．已知抛物线 $y = a x^{2} - 2 a x + a + 2 (a < 0)$ 与 $x$ 轴交于 $M$ ， $N$ 两点，若该抛物线在 $M$ ， $N$ 之间的部分与线段 $M N$ 所围的区域（包括边界）恰有 $5$ 个整点，则 $a$ 的取值范围是（）

A、 $- 4 \leq a < - 3$ B、 $- 3 \leq a < - 2$ C、 $- 2 \leq a < - 1$ D、 $- 1 \leq a < 0$

查看试题解析
5. 定义：[a，b，c]为二次函数y＝ax² $+$ bx $+$ c（a≠0）的特征数，下面给出特征数为[m，1 $-$ m，2 $-$ m]的二次函数的一些结论：①当m＝1时，函数图象的对称轴是y轴；②当m＝2时，函数图象过原点；③当m＞0时，函数有最小值；④如果m＜0，当x＞0.5时，y随x的增大而减小．其中所有正确结论的序号是（）

A、①② B、②③ C、①②③ D、①②③④

查看试题解析
6. 对于某一函数给出如下定义：若存在实数m ，自变量的值为m时，函数值等于-m ，则称-m为这个函数的反向值.在函数存在反向值时，该函数的最大反向值与最小反向值之差n称为这个函数的反向距离.特别地，当函数只有一个反向值时，其反向距离n为零.例如：图中的函数有4，－1两个反向值，其反向距离n等于5.现有函数y＝ ${\begin{matrix} x^{2} - 3 x (x \geq k) \\ - x^{2} - 3 x (x < k) \end{matrix}$ ，则这个函数的反向距离的所有可能值有（）

A、1个 B、2个 C、3个及以上的有限个 D、无数个

查看试题解析
7. 定义：如果抛物线：y=a₁x²+bx+c₁(a₁≠0)与抛物线y=a₂x²+bx+c₂(a₂≠0)满足：a₁+a₂=0，c₁+c₂=0，则称这两条抛物线互为“同胞抛物线”．现有下列结论：①抛物线y=(x+1)²-2的同胞抛物线是抛物线y=(x+1)²+2；②若两条抛物线互为同胞抛物线，则它们的顶点关于原点对称；③已知抛物线C₁与抛物线C₂互为同胞抛物线，若点M(2，3)在抛物线C1上，则N(-3，-2)在抛物线C₂上；④已知抛物线C₁与抛物线C₂互为同胞抛物线。则它们一定有两个不同的交点．
其中正确的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
8. 已知 $y_{1}$ 和 $y_{2}$ 均是以 $x$ 为自变量的函数， $a$ 为实数.当 $x = m$ 时，函数值分别为 $M_{1}$ 和 $M_{2}$ ，若存在实数 $m$ ，使得 $M_{1} = M_{2}$ .则称 $y_{1}$ 和 $y_{2}$ 为友好函数，以下 $y_{1}$ 和 $y_{2}$ 不一定是友好函数的是（）

A、 $y_{1} = x^{2} + 2 x$ 和 $y_{2} = 3 x + 1$ B、 $y_{1} = x^{2} + a - \frac{1}{2}$ 和 $y_{2} = - a x + \frac{a}{4}$ C、 $y_{1} = - \frac{2}{x}$ 和 $y_{2} = x - 3$ D、 $y_{1} = \frac{a + 2}{x}$ 和 $y_{2} = x + a$

查看试题解析

二、填空题

9. 定义[a ， b ， c]为函数y＝ax²+bx+c的特征数，下面给出特征数为[2m ， 1﹣m ， ﹣1﹣m]的函数的一些结论：
①当m＝﹣1时，函数图象的顶点坐标是（ $\frac{1}{2}$ ， $\frac{1}{2}$ ）；

②当m＞0时，函数图象截x轴所得的线段长度大于 $\frac{3}{2}$ ；

③当m＜0时，函数在 $x > \frac{1}{4}$ 时，y随x的增大而减小；

④当m≠0时，函数图象经过x轴上一个定点．

其中正确的结论有．（只需填写序号）

查看试题解析
10. 对于实数a和b，定义运算“*”：a*b= ${\begin{array}{l} a^{2} - a b ， a \leq b \\ b^{2} - a b ， a > b \end{array}$ 设f（x）=（2x-1）*（x-1），且关于x的方程为f（x）=m（m是任意实数）恰有三个互不相等的实数根，则m的取值范围是.

查看试题解析
11. 对于实数a，b，定义运算“*”： $a*b = a^{2} － ab (a \leq b)$ ； $a*b = b^{2} － ab (a > b)$ ，关于x的方程 $(2 x － 1) * (x － 1) = m$ 恰好有三个不相等的实数根，则m的取值范围是．

查看试题解析
12. 如图，直线l： $y = \frac{1}{3} x + \frac{1}{4}$ ，一组抛物线的顶点B₁（1，y₁），B₂（2，y₂），B₃（3，y₃）…B_n（n，y_n）（n为正整数）依次是直线l上的点，这组抛物线与x轴正半轴的交点依次是：A₁（x₁ ， 0），A₂（x₂ ， 0），A₃（x₃ ， 0）…，A_n+1（x_n+1 ， 0）（n为正整数），设x₁=d（0＜d＜1）若其中一条抛物线的顶点与x轴的两个交点构成的三角形是直角三角形，则我们把这条抛物线就称为：“美丽抛物线”.则当d（0＜d＜1）的大小变化时能产生美丽抛物线相应的d的值是.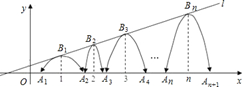

查看试题解析
13. 定义符号max{a，b}的含义为：当a≥b时，max{a，b}＝a；当a＜b时，max{a，b}＝b.如max{1，﹣3}＝1，则max{x²+2x+3，﹣2x+8}的最小值是.

查看试题解析

三、解答题

14. 【定义】在平面直角坐标系中，对“纵横值”给出如下定义：点 $A (x, y)$ 是函数图象上任意一点，纵坐标y与横坐标x的差“ $y - x$ ”称为点A的“纵横值”．函数图象上所有点的“纵横值”中的最大值称为函数的“最优纵横值”．
【举例】已知点 $A (1, 3)$ 在函数 $y = 2 x + 1$ 图象上．点 $A (1, 3)$ 的“纵横值”为 $y - x = 3 - 1 = 2$ ；函数 $y = 2 x + 1$ 图象上所有点的“纵横值”可以表示为 $y - x = 2 x + 1 - x = x + 1$ ，当 $3 \leq x \leq 6$ 时， $x + 1$ 的最大值为 $6 + 1 = 7$ ，所以函数 $y = 2 x + 1 (3 \leq x \leq 6)$ 的“最优纵横值”为7．
【问题】根据定义，解答下列问题：

(1)、①点 $B (- 6, 2)$ 的“纵横值”为；
②求出函数 $y = \frac{4}{x} + x (2 \leq x \leq 4)$ 的“最优纵横值”；

(2)、若二次函数 $y = - x^{2} + b x + c$ 的顶点在直线 $x = \frac{3}{2}$ 上，且最优纵横值为5，求c的值；

(3)、若二次函数 $y = - x^{2} + (2 b + 1) x - b^{2} + 3$ ，当 $- 1 \leq x \leq 4$ 时，二次函数的最优纵横值为2，直接写出b的值．

查看试题解析
15. 定义｛a，b，c｝为函数y=ax² +bx+c的“特征数”.如：函数 $y = x^{2} - 2 x + 3$ 的“特征数”是｛1，-2，3｝.将“特征数”为｛1，-4，1｝的函数图象先向左平移3个单位，再向下平移2个单位得到一个新函数图象，求这个新函数图象的解析式．

查看试题解析
16. 【定义】在平面直角坐标系中，对“纵横值”给出如下定义：点 $A (x, y)$ 是函数图象上任意一点，纵坐标y与横坐标x的差“ $y - x$ ”称为点A的“纵横值”．函数图象上所有点的“纵横值”中的最大值称为函数的“最优纵横值”．
【举例】已知点 $A (1, 3)$ 在函数 $y = 2 x + 1$ 图象上．点 $A (1, 3)$ 的“纵横值”为 $y - x = 3 - 1 = 2$ ；函数 $y = 2 x + 1$ 图象上所有点的“纵横值”可以表示为 $y - x = 2 x + 1 - x = x + 1$ ，当 $3 \leq x \leq 6$ 时， $x + 1$ 的最大值为 $6 + 1 = 7$ ，所以函数 $y = 2 x + 1 (3 \leq x \leq 6)$ 的“最优纵横值”为7．
【问题】根据定义，解答下列问题：

(1)、①点 $B (- 6, 2)$ 的“纵横值”为；
②求出函数 $y = \frac{4}{x} + x (2 \leq x \leq 4)$ 的“最优纵横值”；

(2)、若二次函数 $y = - x^{2} + b x + c$ 的顶点在直线 $x = \frac{3}{2}$ 上，且最优纵横值为5，求c的值；

(3)、若二次函数 $y = - x^{2} + (2 b + 1) x - b^{2} + 3$ ，当 $- 1 \leq x \leq 4$ 时，二次函数的最优纵横值为2，直接写出b的值．

查看试题解析
17. 阅读下列材料，解决材料后的问题：
材料一：对于实数x、y，我们将x与y的“友好数”用f（x，y）表示，定义为： $f (x ， y) = \frac{x}{y + 2}$ ，例如17与16的友好数为 $f (17 ， 16) = \frac{17}{16 + 2} = \frac{17}{18}$ .

材料二：对于实数 $x$ ，用 $[x]$ 表示不超过实数 $x$ 的最大整数，即满足条件 $[x]$ ≤ $x$ ＜ $[x] + 1$ ，例如：

$[- 1.5] = [- 1.6] = - 2$ ， $[0] = [0.7] = 0$ ， $[2.2] = [2.7] = 2$ ，……

(1)、由材料一知： $x^{2} + 2$ 与1的“友好数”可以用 $f (x^{2} + 2 ， 1)$ 表示，已知 $f (x^{2} + 2 ， 1) = 2$ ，请求出 $x$ 的值；

(2)、已知 $[\frac{1}{2} a - 1] = - 3$ ，请求出实数a的取值范围；

(3)、已知实数 $x 、 m$ 满足条件 $x - 2 [x] = \frac{7}{2}$ ，且 $m \geq 2x + \frac{11}{2}$ ，请求 $f (x ， m^{2} - \frac{3}{2} m)$ 的最小值.

查看试题解析
18. 定义：如图1，点 $M$ 、 $N$ 把线段 $A B$ 分割成三条线段 $A M$ 、 $M N$ 和 $B N$ ，若 $M N^{2} = A M · B N$ ，则称 $M N$ 是线段 $A B$ 的比例中段， $M$ 、 $N$ 是线段 $A B$ 的中段分点.

(1)、已知点 $M$ 、 $N$ 是线段 $A B$ 的中段分点.
①若 $A M = 2$ ， $M N = 3$ ，则 $B N =$ ▲ ；
②在图1中，若 $A B = 7$ ， $M N = 2$ ，求 $A M$ 的长.

(2)、如图2，在 $Δ A B C$ 中， $M N$ 是线段 $A B$ 的比例中段， $F$ 、 $G$ 分别是线段 $A C$ 、 $B C$ 延长线上的点，且 $F G ∥ A B$ ， $M C$ 、 $N C$ 的延长线分别交线段 $F G$ 于点 $P$ ， $K$ .探究 $P K$ 是否为线段 $F G$ 的比例中段，如果是，请给出证明，如果不是，请说明理由..

查看试题解析
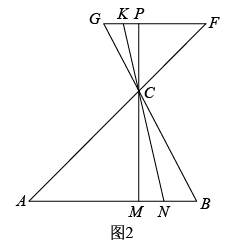19. 如图1，在 $⊙ O$ 中，弦 $A D$ 平分圆周角 $∠ B A C$ ，我们将圆中以A为公共点的三条弦 $B A ， C A ， D A$ 构成的图形称为圆中“爪形A”，如图2，四边形 $A B C D$ 内接于圆， $A B ＝ B C$ ，

(1)、证明：圆中存在“爪形D”；

(2)、若 $∠ A D C ＝ 120 °$ ，求证： $A D ＋ C D ＝ B D$

查看试题解析
20. 若定义：若一个函数图象上存在纵坐标是横坐标2倍的点，则把该函数称为“明德函数”，该点称为“明德点”，例如：“明德函数” $y = x + 1$ ，其“明德点”为 $(1 ， 2)$ .

(1)、①判断：函数 $y = 2 x + 3$ “明德函数”（填“是”或“不是”）；
②函数 $y = x^{2}$ 的图像上的明德点是；

(2)、若抛物线 $y = (m - 1) x^{2} + m x + \frac{1}{4} m$ 上有两个“明德点”，求 $m$ 的取值范围；

(3)、若函数 $y = x^{2} + (m - k + 2) x + \frac{n}{4} - \frac{1}{2} k$ 的图象上存在唯一的一个“明德点”，且当 $- 1 \leq m \leq 3$ 时， $n$ 的最小值为 $k$ ，求 $k$ 的值.

查看试题解析
21. 定义：将函数C的图象绕点P（0，n）旋转180°，得到新的函数C₁的图象，我们称函数C₁是函数C关于点P的相关函数．
例如：当n＝1时，函数y＝ $\frac{1}{2}$ （x﹣6）²+3关于点P（0，1）的相关函数为y＝ $- \frac{1}{2}$ （x+6）²﹣1．

(1)、当n＝0时，
①二次函数y＝x²关于点P的相关函数为；
②点A（2，3）在二次函数y＝ax²﹣2ax+a（a≠0）关于点P的相关函数的图象上，求a的值；

(2)、函数y＝﹣x²+ $\frac{5}{3} \sqrt{2}$ 关于点P的相关函数是y＝x² $- \frac{7}{4} \sqrt{2}$ ，则n＝；

(3)、当 $\frac{3}{4}$ n﹣1≤x≤ $\frac{3}{4}$ n+3时，函数y＝﹣2x²+nx $- \frac{9}{8}$ n²的相关函数的最小值为7，求n的值．

查看试题解析
22. 对于函数定义变换：当y≥0时，函数值不变；当y＜0时，函数值变为原来的相反数，我们把这种变换称为函数的“关联变换”，变换后的函数称为原函数的“关联函数”，“关联函数”与x轴的交点叫做“转折点”．
如：一次函数y＝x－1，关联函数为 $y = {\begin{array}{l} x - 1 (x \geq 1) \\ - x + 1 (x < 1) \end{array}}$ ，这个关联函数的转折点是(1，0)．

(1)、已知一次函数y＝2x－3，请直接写出它的“关联函数”的解析式和转折点．

(2)、已知二次函数y＝x²－2x－3，点(a ， 4)在它的“关联函数”的图象上，求a的值．

(3)、在平面直角坐标系内，有点M(－1，1)、N(3，1)，请直接写出a的取值范围是多少时，二次函数y＝x²－2x＋a的关联函数与线段MN恰有两个公共点．

查看试题解析
23. 如图1，C，D是半圆ACB上的两点，若直径AB上存在一点P，确足∠APC＝∠BPD，则称∠CPD是 $\overset{⌢}{C D}$ 的“美丽角”．

(1)、如图2，AB是⊙O的直径，弦CE⊥AB，D是 $\overset{⌢}{B C}$ 上一点，连结ED交AB于点P，连结CP，∠CPD是 $\overset{⌢}{C D}$ 的“美丽角”吗？请说明理由；

(2)、设 $\overset{⌢}{C D}$ 的度数为α，请用含α的式子表示 $\overset{⌢}{C D}$ 的“美丽角”度数；

(3)、如图3，在（1）的条件下，若直径AB＝5， $\overset{⌢}{C D}$ 的“美丽角”为90°，当 $D E = \frac{7}{2} \sqrt{2}$ 时，求CE的长．

查看试题解析
24. 如图1， $C$ ， $D$ 是半圆 $A C B$ 上的两点，若直径 $A B$ 上存在一点 $P$ ，满足 $∠ A P C = ∠ B P D$ ，则称 $∠ C P D$ 是 $\overset{⌢}{C D}$ 的“幸运角”.

(1)、如图2， $A B$ 是 $⊙ O$ 的直径，弦 $C E ⊥ A B$ ， $D$ 是 $B C$ 上一点，连结 $E D$ 交 $A B$ 于点 $P$ ，连结 $C P$ ， $∠ C P D$ 是 $\overset{⌢}{C D}$ 的“幸运角”吗？请说明理由；

(2)、设 $\overset{⌢}{C D}$ 的度数为 $n$ ，请用含 $n$ 的式子表示 $\overset{⌢}{C D}$ 的“幸运角”度数；

(3)、在（1）的条件下，直径 $A B = 10$ ， $\overset{⌢}{C D}$ 的“幸运角”为 $90 °$ .
①如图3，连结 $C D$ ，求弦 $C D$ 的长；
②当 $D E = 7 \sqrt{2}$ 时，求 $C E$ 的长.

查看试题解析