浙教版数学七上考点突破训练：数轴的左右跳跃、双动点、折线、动态定值模型
试卷更新日期：2024-10-18 类型：复习试卷
一、数轴的左右跳跃模型
-
1. 如图，A点的初始位置在数轴上表示1的点上，先对A做如下移动：第一次向右移动3个单位长度到达点B，第二次从B点出发向左移动6个单位长度到达点 C，第三次从C点出发向右移动9个单位长度到达点D，第四次从D点出发向左移动12个单位长度到达点E，………以此类推，按照以上规律第( )次移动到的点到原点的距离为20.
A、7 B、10 C、14 D、192. 如图，在数轴上，点A表示1，现将点A沿数轴做如下移动：第1次将点A向左移动3个单位长度到达点 ， 第2次将点向右平移6个单位长度到达点 ， 第3次将点向左移动9个单位长度到达点 ， …，按照这种规律移动下去，至少移动次后该点到原点O的距离不小于41．
3. 一个机器人从数轴原点出发，沿数轴正方向，以每前进3步后退2步的程序运动，设该机器人每秒钟前进或后退1步，并且每步的距离为1个单位长度， 表示第 n秒时机器人在数轴上的位置所对应的数.给出下列结论：①；②1；③；④.其中，正确结论的序号是.4. 如图，已知：a、b分别是数轴上两点A、B所表示的有理数，满足|a+20|+（b+8）2＝0．
(1)、求A、B两点相距多少个单位长度？(2)、若C点在数轴上，C点到B点的距离是C点到A点距离的 ， 求C点表示的数；(3)、点P从A点出发，先向左移动一个单位长度，再向右移动2个单位长度，再向左移动3个单位长度，再向右移动4个单位长度，如此下去，依次操作2023次后，求P点表示的数．5. 如图，将一辆小车放在数轴（单位长度为1cm）上，小车左端与数轴上的点A重合，右端与数轴上的点B重合．其中点A ， 点B表示的数分别为a ， b ．
(1)、若将小车沿数轴向右水平移动，则当它的左端移动到点B时，它的右端在数轴上所对应的数为27；若将小车沿数轴向左水平移动，则当它的右端移动到点A时，它的左端在数轴上所对应的数为6，由此可得a＝ ， b＝ ．(2)、若P为数轴上一动点，其对应的数为x ， 若|x+a|+|x﹣b|＝42，则x的值为 ．(3)、动点P从点A出发向右以每秒1个单位的速度匀速运动，同时另一动点Q恰好从B点出发，以3个单位/秒的速度也向左运动，请问：经过多少时间时，PQ的距离为5个单位长度？二、数轴的双动点模型
-
6. 如图，在数轴上，点A，B分别表示﹣15，9，点P，Q分别从点A，B同时开始沿数轴正方向运动，点P的速度是每秒3个单位，点Q的速度是每秒1个单位，运动时间为t秒，在运动过程中，当点P，点Q和原点O这三点中的一点恰好是另外两点为端点的线段的中点时，则满足条件整数t的值（ ）
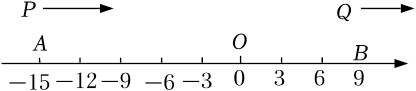A、22 B、33 C、44 D、557. 如图，在数轴上，点 ， 点表示的数分别是 ， 点以个单位秒的速度从出发沿数轴向右运动，同时点以个单位秒的速度从点出发沿数轴在 ， 之间往返运动当点到达点时，点表示的数是 ．
8. 如图，点和点在数轴上，点在原点的左侧，点在原点的右侧，点表示的数是6，用表示点与点之间的距离，用表示点与点之间的距离，用表示点和点之间的距离，且.动点从点出发以每秒4个单位长度的速度沿数轴负方向运动，同时动点从原点出发以每秒1个单位长度的速度沿数轴负方向运动；当动点到达点时， ， 两点同时停止运动.设点的运动时间为秒，用表示点与点之间的距离，用表示点与点之间的距离.
(1)、当点在点的右侧且时，.(2)、当点在点的左侧且时，.9. 已知a、b为常数，且关于x、y的多项式-3) 的值与字母x取值无关，其中a、b分别为点A、点B在数轴上表示的数，如图所示. 动点E、F分别从A、B同时开始运动，点E以每秒6个单位向左运动，点F以每秒2个单位向右运动，设运动时间为t秒.(1)、求a、b的值；(2)、请用含t的代数式表示点E在数轴上对应的数为： ， 点F在数轴上对应的数为：.(3)、当E、F相遇后，点E继续保持向左运动，点F在原地停留4秒后向左运动且速度变为原来的5倍.在整个运动过程中，当E、F之间的距离为2个单位时，求运动时间t的值(不必写过程) .
三、数轴的折线模型
-
10. 数轴上A ， B两点表示的数分别为-6 ，5，点C是线段AB上的一个动点，以点C为折点，将数轴向左对折，点B的对应点落在数轴上的B'处，若B'A=1，则点C表示的数是 ．
11. 一条数轴上有点A、B、C（图①），其中点A、C表示的数分别是-14、6，现以点B为点，将数轴向右对折，若点A对应的点M落在点B的右边、点C的左边，并且C、M两点的距离是6（图②），则点B表示的数是（ ）
A、-6 B、-7 C、-5 D、012. 如下图，数轴上，点A表示的数为-7，点B表示的数为-1，点C表示的数为9，点D表示的数为13，在点B和点C处各折一下，得到一条“折线数轴”，我们称点A和点D在数轴上相距20个长度单位，动点P从点A出发，沿着“折线数轴”的正方向运动，同时，动点Q从点D出发，沿着“折线数轴”的负方向运动，它们在“水平路线”射线BA和射线CD上的运动速度相同均为2个单位/秒，“上坡路段”从B到 C速度变为“水平路线”速度的一半，“下坡路段”从C到 B速度变为“水平路线”速度的2倍. 设运动的时间为t秒，问：
(1)、动点Q从点C运动到点B需要的时间为秒；(2)、动点P从点A 运动至 D点需要的时间为多少秒?(3)、当P、O两点在数轴上相距的长度与Q、O两点在数轴上相距的长度相等时，求出动点P在数轴上所对应的数.13. 七年级数学兴趣小组成员自主开展数学微项目研究，他们决定研究“折线数轴”．探索“折线数轴”
素材1 如图，将一条数轴在原点O，点B，点C处折一下，得到一条“折线数轴”．图中点A表示－9，点B表示12，点C表示24，点D表示36，我们称点A与点D在数轴上的“友好距离”为45个单位长度，并表示为 ．
素材2 动点P从点A出发，以2个单位长度/秒的初始速度沿着“折线数轴”向其正方向运动．当运动到点O与点B之间时速度变为初始速度的一半．当运动到点B与点C之间时速度变为初始速度的两倍．经过点C后立刻恢复初始速度．
问题解决
(1)、探索1 动点P从点A运动至点B需要多少时间？(2)、探索2 动点P从点A出发，运动t秒至点B和点C之间时，求点P表示的数（用含t的代数式表示）；(3)、探索3 动点P从点A出发，运动至点D的过程中某个时刻满足时，求动点P运动的时间．四、数轴的动态定值（无参型）模型
-
14. 如图，已知A，B(B在A的左侧)是数轴上的两点，点A对应的数为4，且AB=6，动点P从点A出发，以每秒2个单位长度的速度沿数轴向左运动，在点P的运动过程中，M，N始终为AP，BP的中点，设运动时间为)秒，则下列结论中正确的有 ( )
①B对应的数是2； ②点P到达点B时，t=3；③BP=2时，； ④在点 P的运动过程中，线段MN的长度不变.
A、①③④ B、②③④ C、②③ D、②④15. 已知a、b满足 ， 且有理数a、b、c在数轴上对应的点分别为A、B、C.
(1)、则a= ， b= ， c=.(2)、点D是数轴上A点右侧一动点，点E、点F分别为CD、AD中点，当点D运动时，线段EF的长度是否发生变化，若变化，请说明理由，若不变，请求出其值；(3)、若点A、B、C在数轴上运动，其中点C以每秒1个单位的速度向左运动，同时点A和点B分别以每秒3个单位和每秒2个单位的速度向右运动·请问：是否存在一个常数m使得m·AB-2BC不随运动时间t的改变而改变·若存在，请求出m和这个不变化的值；若不存在，请说明理由.16. 如图，A、B两点在数轴上对应的数分别为-20、40，在 A、B两点处各放一个挡板，M、N两个电子小球同时从原点出发，M以2个单位/秒的速度向数轴负方向运动，N以4个单位/秒的速度向数轴正方向运动，碰到挡板后则反方向运动，速度大小不变，当两小球第一次相遇时都停止运动. 设两个小球运动的时间为t，那么：
(1)、当0<t<10时，M在数轴上对应的数可以表示为；(2)、小杨同学发现：当0<t<10时，2MB-NA始终为定值.小杨的发现是否正确?若正确，请求出这个定值；若不正确，请说明理由.(3)、在整个运动过程中，t为何值时M、N两个小球间的距离为6?请直接写答案.17. 数形结合是数学解题中的一种重要思想，利用数轴可以将数与形完美结合.一般地，数轴上越往右边的点表示的数越大，例如：若数轴上点M表示数m，则点M向右移动n个单位到达的点N表示的数为m+n，若点M向左移动n个单位到达的点表示的数为m-n.如图1，已知数轴上点A表示的数为10，点B与点A距离18个单位，且在点A的左边，动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t(t>0)秒.
(1)、数轴上点B表示的数为 ， 点P表示的数为. (用含t的式子表示) ；(2)、动点Q从点B出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P，Q同时出发.①求点P运动多少秒追上点Q?②求点 P运动多少秒时与点Q相距6个单位?并求出此时点P表示的数；
(3)、如图2，若点P，Q以(2) 中的速度同时分别从点A，B向右运动，同时点R从原点O以每秒4个单位的速度向右运动，是否存在常数m，使得QR-OP+mOR为定值，若存在，请求出m的值以及这个定值；若不存在，请说明理由. (其中QR 表示数轴上点Q与点R之间的距离，OP 表示数轴上点O与点P的距离，OR表示数轴上点O与点R的距离. )