菱形的性质与判定——北师大版数学九年级上册知识点训练
试卷更新日期:2024-10-17 类型:复习试卷
一、选择题
-
1. 下列命题是真命题的是( )A、有两边相等的平行四边形是菱形 B、对角线互相平分的四边形是平行四边形 C、四个角都相等的平行四边形是正方形 D、有一个角是直角的四边形是矩形2. 如图,菱形中,连接 , 若 , 则的度数为( )
 A、 B、 C、 D、3. 如图,菱形ABCD中,∠BAD = 60°,AB = 6,点E,F分别在边AB,AD上,将△AEF沿EF翻折得到△GEF,若点G恰好为CD边的中点,则AE的长为( )
A、 B、 C、 D、3. 如图,菱形ABCD中,∠BAD = 60°,AB = 6,点E,F分别在边AB,AD上,将△AEF沿EF翻折得到△GEF,若点G恰好为CD边的中点,则AE的长为( )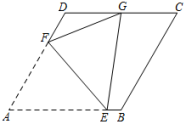 A、 B、 C、 D、34. 如图,在平面直角坐标系中,菱形 , 为坐标原点,点在轴上,的坐标为 , 则顶点的坐标是( )
A、 B、 C、 D、34. 如图,在平面直角坐标系中,菱形 , 为坐标原点,点在轴上,的坐标为 , 则顶点的坐标是( ) A、 B、 C、 D、5. 如图,在菱形ABCD中,AB=5,AC=6,过点D作DE⊥BA,交BA的延长线于点E,则线段DE的长为( )
A、 B、 C、 D、5. 如图,在菱形ABCD中,AB=5,AC=6,过点D作DE⊥BA,交BA的延长线于点E,则线段DE的长为( ) A、 B、 C、4 D、6. “蓝丝带”一般指蓝丝带海洋保护协会,同时也象征着对保护海洋的呼吁.李老师用一段矩形绸缎制作了一条如图所示宽为的蓝丝带,若 , 则重叠部分图形形状和面积分别是( )
A、 B、 C、4 D、6. “蓝丝带”一般指蓝丝带海洋保护协会,同时也象征着对保护海洋的呼吁.李老师用一段矩形绸缎制作了一条如图所示宽为的蓝丝带,若 , 则重叠部分图形形状和面积分别是( ) A、平行四边形, B、平行四边形, C、菱形, D、菱形,7. 如图,菱形ABCD中,分别是BC,CD的中点,连接的周长为 , 则菱形ABCD的周长为( )
A、平行四边形, B、平行四边形, C、菱形, D、菱形,7. 如图,菱形ABCD中,分别是BC,CD的中点,连接的周长为 , 则菱形ABCD的周长为( ) A、5cm B、6cm C、 D、8cm8. 如图,在菱形ABCD中,E、F分别是边CD、BC上的动点,连接AE , EF , G、H分别为AE、EF的中点,连接GH . 若∠D=45°,AD=4,则GH的最小值为( )
A、5cm B、6cm C、 D、8cm8. 如图,在菱形ABCD中,E、F分别是边CD、BC上的动点,连接AE , EF , G、H分别为AE、EF的中点,连接GH . 若∠D=45°,AD=4,则GH的最小值为( ) A、2 B、4 C、 D、
A、2 B、4 C、 D、二、填空题
-
9. 已知菱形的两条对角线分别是和 , 则其面积是 .10. 如图,在菱形中,对角线、交于点 , 作交的延长线于点 , 连接 , 若 , , 则菱形的面积为 .
 11. 如图,菱形的边长为4, , 过点B作交于点E,连接 , F为的中点,连接 , 交于点G,则的长为 .
11. 如图,菱形的边长为4, , 过点B作交于点E,连接 , F为的中点,连接 , 交于点G,则的长为 . 12. 如图,在菱形ABCD中,过点B作BE⊥AD,BF⊥CD,垂足分别为点E,F,延长BD至G,使得DG=BD,连结EG,FG,若AE=DE,则 = .
12. 如图,在菱形ABCD中,过点B作BE⊥AD,BF⊥CD,垂足分别为点E,F,延长BD至G,使得DG=BD,连结EG,FG,若AE=DE,则 = . 13. 如图,在矩形ABCD中,AB=6.点P , 点Q同时从点A出发,沿AB方向匀速运动,点P的速度为1,点Q的速度为3,点Q到达点B时停留在点B , 待点P继续运动到点B时结束运动.设运动时间为t , 已知当t=1时,线段DC上有一点M , 使四边形PQMD是菱形.若运动过程中,线段DC上另有一点N , 使四边形PQND是菱形,则此时t= .
13. 如图,在矩形ABCD中,AB=6.点P , 点Q同时从点A出发,沿AB方向匀速运动,点P的速度为1,点Q的速度为3,点Q到达点B时停留在点B , 待点P继续运动到点B时结束运动.设运动时间为t , 已知当t=1时,线段DC上有一点M , 使四边形PQMD是菱形.若运动过程中,线段DC上另有一点N , 使四边形PQND是菱形,则此时t= .
三、解答题
-
14. 如图是由个形状大小完全相同的小长方形组成的矩形网格,顶点称为这个矩形网格的格点,请按要求在矩形网格中画格点四边形.
 (1)、在图中画出一个以为对角线的平行四边形 .(2)、若小长方形的宽为 , 请在图中画出一个边长为的菱形注:图 , 图在答题纸上.15. 如图,在中, , , , 点D从点C出发沿方向以的速度向点A匀速运动,同时点E从点A出发沿方向以的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒 . 过点D作于点F,连接、 .
(1)、在图中画出一个以为对角线的平行四边形 .(2)、若小长方形的宽为 , 请在图中画出一个边长为的菱形注:图 , 图在答题纸上.15. 如图,在中, , , , 点D从点C出发沿方向以的速度向点A匀速运动,同时点E从点A出发沿方向以的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒 . 过点D作于点F,连接、 .
备用图
(1)、四边形能够成为菱形吗?如果能,求出相应的t值;如果不能,请说明理由;(2)、四边形能够成为正方形吗?如果能,求出相应的t值;如果不能,请说明理由.16. 如图,在四边形ABCD中, , O为对角线AC的中点,过点O作直线分别与四边形ABCD的边AD , BC交于M , N两点,连接CM , AN . (1)、求证:四边形ANCM为平行四边形;(2)、当MN平分∠AMC时,
(1)、求证:四边形ANCM为平行四边形;(2)、当MN平分∠AMC时,①求证:四边形ANCM为菱形;
②当四边形ABCD是矩形时,若 , , 求DM的长.
17. .如图,在平面直角坐标系中,直线:分别与轴、轴交于点 , , 且与直线:交于点 . (1)、分别求出点 , , 的坐标.(2)、若是线段上的点,且的面积为 , 求直线的函数解析式.(3)、在的条件下,设是射线上的点,在平面内是否存在点 , 使以 , , , 为顶点的四边形是菱形?若存在,求出点的坐标;若不存在,请说明理由.
(1)、分别求出点 , , 的坐标.(2)、若是线段上的点,且的面积为 , 求直线的函数解析式.(3)、在的条件下,设是射线上的点,在平面内是否存在点 , 使以 , , , 为顶点的四边形是菱形?若存在,求出点的坐标;若不存在,请说明理由.
18. 如图所示四边形ABCD的对角线AC、BD交于点O , 已知点 , , BD平分.

图1 图2
(1)、证明:四边形ABCD是菱形;(2)、如图1,过四边形ABCD的顶点作 , 且 , 线段交于点 , 交于点 , 交的延长线于点 , 求证:;(3)、如图2,在四边形中,若 , 的面积为 , 点是直线上一动点,连接.点在线段的左侧,为等边三角形,连接 , 当线段最短时,求的值.19. 综合与实践顺次连接任意一个四边形的中点得到一个新四边形,我们称这个新四边形为原四边形的中点四边形 . 数学兴趣小组通过作图、测量,猜想:原四边形的对角线对中点四边形的形状有着决定性作用.
以下从对角线的数量关系和位置关系两个方面展开探究.
【探究一】
原四边形对角线关系
中点四边形形状

不相等、不垂直
平行四边形
如图1,在四边形中,E、F、G、H分别是各边的中点.
求证:中点四边形是平行四边形.
证明:∵E、F、G、H分别是、、、的中点,
∴、分别是和的中位线,
∴ , ( ① )
∴ .
同理可得: .
∴中点四边形是平行四边形.
结论:任意四边形的中点四边形是平行四边形.
(1)、请你补全上述过程中的证明依据.(2)、【探究二】原四边形对角线关系
中点四边形形状

不相等、不垂直
平行四边形
菱形
从作图、测量结果得出猜想Ⅰ:原四边形的对角线相等时,中点四边形是菱形.
下面我们结合图2来证明猜想Ⅰ,请你在探究一证明结论的基础上,写出后续的证明过程.(3)、【探究三】
从作图、测量结果得出猜想Ⅱ:原四边形对角线垂直时,中点四边形是 .原四边形对角线关系
中点四边形形状

不相等、不垂直
平行四边形
②
(4)、下面我们结合图3来证明猜想Ⅱ,请你在探究一证明结论的基础上,写出后续的证明过程.(5)、【归纳总结】
请你根据上述探究过程,补全下面的结论,并在图4中画出对应的图形.原四边形对角线关系
中点四边形形状

③
④
结论:原四边形对角线时,中点四边形是 .
20. 综合与实践【问题情境】
如图,在正方形中,点在线段上,点在线段上,且始终满足.连接 , , 将线段绕点逆时针旋转一定角度,得到线段(点是点旋转后的对应点),并使点落在线段上,与交于点.
 (1)、【初步分析】
(1)、【初步分析】线段与的数量关系为 , 位置关系为;
(2)、【深入分析】如图②,再将线段绕点逆时针旋转90°,得到线段(点是点旋转后的对应点),连接 , 请判断四边形的形状,并说明理由:
(3)、如图③,若点落在的延长线上,且当点恰好为的中点时,设与交于点 , , 求的长.