人教版数学九年级全册知识点训练营——圆内接四边形
试卷更新日期:2024-10-16 类型:复习试卷
一、夯实基础
-
1. 如图,圆内接四边形两组对边的延长线分别相交于点E,F,且 , 那么的度数为 .

二、能力提升
-
2. 如图,△ACD≌△ACB≌△AEB , 将这三个三角形按照图中所示摆放在圆内,点A , E , B , D四点在圆上,若∠BCD=112°,则∠BAD的度数是( )
 A、72° B、68° C、56° D、34°
A、72° B、68° C、56° D、34°三、拓展创新
-
3. 如图,在四边形中, , 以为腰作等腰直角三角形 , 顶点恰好落在边上,若 , 则的长是( )
 A、 B、 C、2 D、14. 如图,在中, , , , 点P是延长线上一动点,边与点M,边与点N,连接 , 则的最小值为( )
A、 B、 C、2 D、14. 如图,在中, , , , 点P是延长线上一动点,边与点M,边与点N,连接 , 则的最小值为( )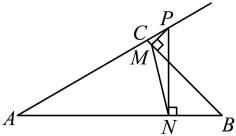 A、 B、 C、 D、5. 如图,已知四边形是矩形, , 点E是线段上一个动点,分别以、为边向线段的下方作正方形、正方形 , 连接 , 过点B作直线的垂线,垂足是J , 连接 , 求点E运动过程中,线段的最大值是 .
A、 B、 C、 D、5. 如图,已知四边形是矩形, , 点E是线段上一个动点,分别以、为边向线段的下方作正方形、正方形 , 连接 , 过点B作直线的垂线,垂足是J , 连接 , 求点E运动过程中,线段的最大值是 . 6. 如图,是的直径,弦与点 , 已知 , 点为上任意一点,(点不与重合),连结并延长与交于点 , 连 .
6. 如图,是的直径,弦与点 , 已知 , 点为上任意一点,(点不与重合),连结并延长与交于点 , 连 .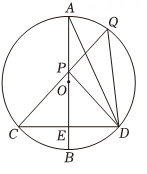 (1)、求的长.(2)、若 , 直接写出的长.(3)、①若点在之间(点不与点重合),求证: .
(1)、求的长.(2)、若 , 直接写出的长.(3)、①若点在之间(点不与点重合),求证: .②若点在之间(点不与点重合),求与满足的关系.
7. 综合与实践:“善思”小组开展“探究四点共圆的条件”活动,得出结论:对角互补的四边形四个顶点共圆.该小组继续利用上述结论进行探究.
提出问题:
如图1所示,在线段同侧有两点 , , 连接 , , , , 如果 , 那么 , , , 四点在同一个圆上.

探究展示:
如图2所示,作经过点 , , 的 , 在劣弧上取一点(不与 , 重合),连接 , ,

则 , (依据
,
,
点 , , , 四点在同一个圆上,(对角互补的四边形四个顶点共圆)
点 , 在点 , , 所确定的上,(依据
点 , , , 四点在同一个圆上;
反思归纳:
(1)上述探究过程中的“依据1”、“依据2”分别是指什么?
依据1:______;(从右边框内选一个选项,直接填序号)
依据2:______.(从右边框内选一个选项,直接填序号)
①圆内接四边形对角互补;
②对角互补的四边形四个顶点共圆;
③过不在同一直线上的三个点有且只有一个圆;
④经过两点的圆的圆心在这两点所连线段的垂直平分线上;
(2)如图3所示,在四边形中, , , 则的度数为______.

-
-