人教版数学九年级全册知识点训练营——二次函数与坐标轴的交点问题
试卷更新日期:2024-10-16 类型:复习试卷
一、夯实基础
-
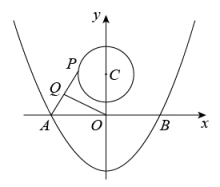
1. 如图,过点D(1,3)的抛物线y=-x2+k的顶点为A,与x轴交于B、C两点,若点P是y轴上一点,则PC+PD的最小值为 .
 2. 把二次函数的图像沿y轴向上平移1个单位长度,与y轴的交点为C,则C点坐标是 .
2. 把二次函数的图像沿y轴向上平移1个单位长度,与y轴的交点为C,则C点坐标是 .二、能力提升
-
3. 已知函数 的图象与x轴有交点.则 的取值范围是( )A、k<4 B、k≤4 C、k<4且k≠3 D、k≤4且k≠34. 如图是抛物线图象的一部分,抛物线的顶点是 , 对称轴是直线 , 且抛物线与轴的一个交点为;直线的解析式为下列结论:

;
;
方程有两个不相等的实数根;
抛物线与轴的另一个交点是;
当时,则 , 其中正确的是( )
A、 B、 C、 D、三、拓展创新
-
5. 如图,已知开口向下的抛物线与轴交于点 , 对称轴为直线则下列结论:;;;抛物线上有两点和 , 若且 , 则其中正确的有( )
 A、个 B、个 C、个 D、个6. 二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣2,0)对称轴为直线x=1,下列结论:①abc<0;②2a﹣b=0;③b2﹣4ac>0;④当y>0时,x的取值范围是﹣2<x<4;⑤9a+c>3b , 其中正确的结论序号为( )
A、个 B、个 C、个 D、个6. 二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣2,0)对称轴为直线x=1,下列结论:①abc<0;②2a﹣b=0;③b2﹣4ac>0;④当y>0时,x的取值范围是﹣2<x<4;⑤9a+c>3b , 其中正确的结论序号为( ) A、①②③ B、①③④ C、①③④⑤ D、②③④
A、①②③ B、①③④ C、①③④⑤ D、②③④