人教版数学九年级全册知识点训练营——二次函数图象的翻折
试卷更新日期:2024-10-16 类型:复习试卷
一、夯实基础
-
1. 如图,将二次函数的图象在轴上方的部分沿轴翻折到轴下方,图象的其余部分保持不变,得到一个新图象,则新图象与直线的交点个数为( )
 A、1 B、2 C、3 D、42. 小嘉说:将二次函数 的图象平移或翻折后经过点 有下列 4 种方法:
A、1 B、2 C、3 D、42. 小嘉说:将二次函数 的图象平移或翻折后经过点 有下列 4 种方法:①向右平移 2 个单位;②先向右平移 1 个单位,再向下平移 1 个单位; ③向下平移 4 个单位; ④先沿 轴翻折, 再向上平移 4 个单位.
你认为小嘉说的方法中正确的有( )
A、1 个 B、2 个 C、3 个 D、4 个3. 与抛物线关于x轴对称的抛物线的解析式表示为( )A、 B、 C、 D、4. 已知二次函数y=﹣x2+x+6,将该二次函数在x轴上方的图象沿x轴翻折到x轴下方,图象的其余部分不变,得到一个新的函数图象(如图所示),当直线y=﹣x+m与新图象有3个交点时,m的值是( ) A、 B、﹣2 C、﹣2或3 D、﹣6或﹣25. 如图,在平面直角坐标系中,将函数y=x2-2x的图象先沿x轴翻折,再向上平移5个单位长度,得到的抛物线所对应的函数表达式是( )
A、 B、﹣2 C、﹣2或3 D、﹣6或﹣25. 如图,在平面直角坐标系中,将函数y=x2-2x的图象先沿x轴翻折,再向上平移5个单位长度,得到的抛物线所对应的函数表达式是( ) A、 B、 C、 D、6. 在平面直角坐标系中,将二次函数y=x2+2x-1的图象先沿x轴翻折,再向下平移3个单位,所得到的新的函数图象的解析式是 .
A、 B、 C、 D、6. 在平面直角坐标系中,将二次函数y=x2+2x-1的图象先沿x轴翻折,再向下平移3个单位,所得到的新的函数图象的解析式是 .二、能力提升
-
7. 已知抛物线L: , 其中顶点为 , 与轴交于点 , 将抛物线L绕原点旋转180°,点、的对应点分别为、 , 若四边形为矩形,则的值为( )A、 B、 C、 D、8. 如图是函数y=x2﹣2x﹣3(0≤x≤4)的图象,直线l∥x轴且过点(0,m),将该函数在直线l上方的图象沿直线l向下翻折,在直线l下方的图象保持不变,得到一个新图象.若新图象对应的函数的最大值与最小值之差不大于5,则m的取值范围是( )
 A、m≥1 B、m≤0 C、0≤m≤1 D、m≥1或m≤09. 如图, 将抛物线沿轴翻折, 翻折前后的两条抛物线构成一个新图象.若直线与这个新图象有3个公共点, 则的值为( )
A、m≥1 B、m≤0 C、0≤m≤1 D、m≥1或m≤09. 如图, 将抛物线沿轴翻折, 翻折前后的两条抛物线构成一个新图象.若直线与这个新图象有3个公共点, 则的值为( ) A、或2 B、或2 C、2或4 D、或410. 抛物线y=x²+2x-3与x轴相交于A、B两点,其顶点为M,将此抛物线在x轴下方的部分沿x轴翻折,其余部分保持不变,得到一个新的图象,如图.在这个新图象上有一点P,能使得S△ABP=6,则点P的坐标为.
A、或2 B、或2 C、2或4 D、或410. 抛物线y=x²+2x-3与x轴相交于A、B两点,其顶点为M,将此抛物线在x轴下方的部分沿x轴翻折,其余部分保持不变,得到一个新的图象,如图.在这个新图象上有一点P,能使得S△ABP=6,则点P的坐标为.
三、拓展创新
-
11. 已知抛物线与抛物线关于点成中心对称,若当时,有最大值为4,则的值为( )A、 B、-6 C、 D、-6或12. 把二次函数的图象作关于原点的对称变化,所得到的图象函数式为 , 若 , 则m最小值是( )A、6 B、4 C、8 D、213. 如图,在平面直角坐标中,将抛物线y=﹣2x2+2x在x轴上方的部分进行循环反复的轴对称或中心对称变换,若点A是该抛物线的顶点,则经过第2023次变换后所得的A点的坐标是 .
 14. 将抛物线位于轴左侧的部分沿轴翻折,其余部分不变,翻折得到的图象和原来不变的部分构成一个新图象,若直线与新图象有且只有2个公共点,则的取值范围是( )A、 B、 C、或 D、或15. 已知二次函数y=x2-2x+m的图象C与y轴交于点M,过点M作直线l平行于x轴,将抛物线C位于直线l下方的部分翻折至直线l上方.若变换后的图象与x轴有4个交点,则m的取值范围为( )A、m>—1 B、-1<m<0 C、-1≤m≤0 D、-1≤m<016. 如图,把二次函数的图象在x轴上方的部分沿着x轴翻折,得到的新函数叫做的“陷阱”函数.小明同学画出了的“陷阱”函数的图象,如图所示并写出了关于该函数的4个结论,其中正确结论的个数为( )
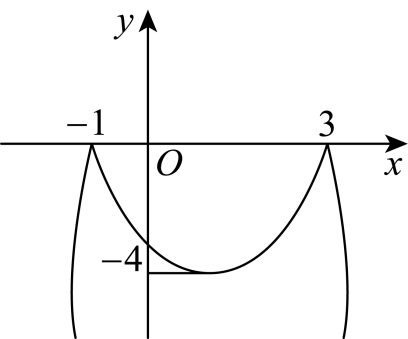
14. 将抛物线位于轴左侧的部分沿轴翻折,其余部分不变,翻折得到的图象和原来不变的部分构成一个新图象,若直线与新图象有且只有2个公共点,则的取值范围是( )A、 B、 C、或 D、或15. 已知二次函数y=x2-2x+m的图象C与y轴交于点M,过点M作直线l平行于x轴,将抛物线C位于直线l下方的部分翻折至直线l上方.若变换后的图象与x轴有4个交点,则m的取值范围为( )A、m>—1 B、-1<m<0 C、-1≤m≤0 D、-1≤m<016. 如图,把二次函数的图象在x轴上方的部分沿着x轴翻折,得到的新函数叫做的“陷阱”函数.小明同学画出了的“陷阱”函数的图象,如图所示并写出了关于该函数的4个结论,其中正确结论的个数为( )①图象具有对称性,对称轴是直线; ②由图象得 , , ;③该“陷阱”函数与y轴交点坐标为;④的“陷阱”函数与的“陷阱”函数的图象是完全相同的.
 A、1 B、2 C、3 D、417. 将二次函数 的图象先向右平移一个单位,再沿x轴翻折到第一象限,然后向右平移一个单位,再沿y轴翻折到第二象限… 以此类推,如果把向右平移一个单位再沿坐标轴翻折一次记作1次变换,那么二次函数 的图象经过2019次变换后,得到的图象的函数解析式为
A、1 B、2 C、3 D、417. 将二次函数 的图象先向右平移一个单位,再沿x轴翻折到第一象限,然后向右平移一个单位,再沿y轴翻折到第二象限… 以此类推,如果把向右平移一个单位再沿坐标轴翻折一次记作1次变换,那么二次函数 的图象经过2019次变换后,得到的图象的函数解析式为