人教版数学九年级全册知识点训练营——二次函数的图象共存问题
试卷更新日期:2024-10-15 类型:复习试卷
一、二次函数图象与一次函数图象共存问题
-
1. 函数y=ax2与y=-ax+b的图象可能是( )A、
 B、
B、 C、
C、 D、
D、 2. 抛物线和直线在同一坐标系内的图像如图,其中正确的是( )A、
2. 抛物线和直线在同一坐标系内的图像如图,其中正确的是( )A、 B、
B、 C、
C、 D、
D、 3. 二次函数的图象如图所示,则一次函数的图象不经过 .
3. 二次函数的图象如图所示,则一次函数的图象不经过 . 4. 二次函数y=a(x+m)2+n的图象如图,则一次函数y=mx+n的图象不经过第象限.
4. 二次函数y=a(x+m)2+n的图象如图,则一次函数y=mx+n的图象不经过第象限. 5. 已知一次函数y1=6x,二次函数y2=3x2+3,是否存在二次函数y3=x2+bx+c,其图象经过点(﹣4,1),且对于任意实数x的同一个值,这三个函数对应的函数值y1 , y2 , y3都有y1≤y2≤y3成立?若存在,求出函数y3的解析式;若不存在,请说明理由.
5. 已知一次函数y1=6x,二次函数y2=3x2+3,是否存在二次函数y3=x2+bx+c,其图象经过点(﹣4,1),且对于任意实数x的同一个值,这三个函数对应的函数值y1 , y2 , y3都有y1≤y2≤y3成立?若存在,求出函数y3的解析式;若不存在,请说明理由.
二、二次函数函数与反比例函数图象共存问题
-
6. 反比例函数 的图象如图所示,则二次函数y=2kx2﹣4x+k2的图象大致是( )
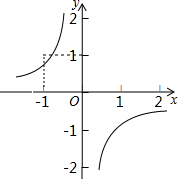 A、
A、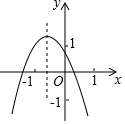 B、
B、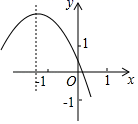 C、
C、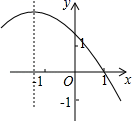 D、
D、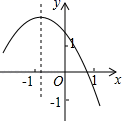 7. 已知反比例函数的图象如图所示,则二次函数的图象大致为( )
7. 已知反比例函数的图象如图所示,则二次函数的图象大致为( ) A、
A、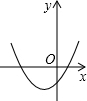 B、
B、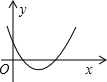 C、
C、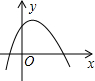 D、
D、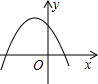 8. 若二次函数 的对称轴是直线 ,则反比例函数 经过第象限.9. 已知二次函数y=ax2+bx+c(a,b,c是常数)的图象如图所示,则反比例函数y= 的图象所在的象限是第象限.
8. 若二次函数 的对称轴是直线 ,则反比例函数 经过第象限.9. 已知二次函数y=ax2+bx+c(a,b,c是常数)的图象如图所示,则反比例函数y= 的图象所在的象限是第象限.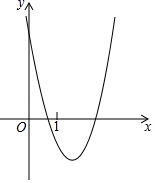
三、一次、反比例、二次函数图象共存问题
-
10. 一次函数 , 二次函数 , 反比例函数在同一直角坐标系中图象如图所示,则n的取值范围是( )
 A、 B、 C、 D、11. 王老师在上函数复习课时,利用列表法给出了变量x,y的三组对应值如下表,你觉得这三点可以同时位于( )的图象上.
A、 B、 C、 D、11. 王老师在上函数复习课时,利用列表法给出了变量x,y的三组对应值如下表,你觉得这三点可以同时位于( )的图象上.x
……
1
2
4
……
y
……
……
A、一次函数和反比例函数 B、二次函数和反比例函数 C、一次函数和二次函数 D、一次函数和二次函数和反比例函数12. 二次函数的图象如图所示,则一次函数与反比例函数的图象可能是( ) A、
A、 B、
B、 C、
C、 D、
D、
四、两二次函数图象综合
-
13. 两个不同的二次函数与的图象有相同的对称轴,则下列结论不正确的是( )A、这两个函数图象的开口方向相反 B、这两个函数图象的都经过点 C、这两个函数图象的关于轴对称 D、二次函数的最大值为14.
如果两个二次函数图象的形状相同,开口方向相同,那么它们的二次项系数相等;
如果两个二次函数图象的形状相同,开口方向相反,那么它们的二次项系数是互为相反数.
已知,在平面直角坐标系中,点的坐标为 , 点的坐标为 . 抛物线上有一点 , 以点为顶点的抛物线经过点(点与点不重合),抛物线和形状相同,开口方向相反.
 (1)、当抛物线经过点时,求抛物线的表达式;(2)、求抛物线的对称轴;(3)、当时,设抛物线的顶点为 , 抛物线的对称轴与轴的交点为 , 联结、、 , 求证:平分 .
(1)、当抛物线经过点时,求抛物线的表达式;(2)、求抛物线的对称轴;(3)、当时,设抛物线的顶点为 , 抛物线的对称轴与轴的交点为 , 联结、、 , 求证:平分 .