数轴的双动点、折线模型模型—人教版数学七(上)知识点训练
试卷更新日期:2024-10-15 类型:复习试卷
一、选择题
-
1. 如图,在数轴上,点A,B分别表示﹣15,9,点P,Q分别从点A,B同时开始沿数轴正方向运动,点P的速度是每秒3个单位,点Q的速度是每秒1个单位,运动时间为t秒,在运动过程中,当点P,点Q和原点O这三点中的一点恰好是另外两点为端点的线段的中点时,则满足条件整数t的值( )
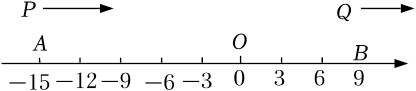 A、22 B、33 C、44 D、55
A、22 B、33 C、44 D、55二、填空题
-
2. 数轴上A , B两点表示的数分别为-6 ,5,点C是线段AB上的一个动点,以点C为折点,将数轴向左对折,点B的对应点落在数轴上的B'处,若B'A=1,则点C表示的数是 .
 3. 如图,点和点在数轴上,点在原点的左侧,点在原点的右侧,点表示的数是6,用表示点与点之间的距离,用表示点与点之间的距离,用表示点和点之间的距离,且.动点从点出发以每秒4个单位长度的速度沿数轴负方向运动,同时动点从原点出发以每秒1个单位长度的速度沿数轴负方向运动;当动点到达点时, , 两点同时停止运动.设点的运动时间为秒,用表示点与点之间的距离,用表示点与点之间的距离.
3. 如图,点和点在数轴上,点在原点的左侧,点在原点的右侧,点表示的数是6,用表示点与点之间的距离,用表示点与点之间的距离,用表示点和点之间的距离,且.动点从点出发以每秒4个单位长度的速度沿数轴负方向运动,同时动点从原点出发以每秒1个单位长度的速度沿数轴负方向运动;当动点到达点时, , 两点同时停止运动.设点的运动时间为秒,用表示点与点之间的距离,用表示点与点之间的距离. (1)、当点在点的右侧且时,.(2)、当点在点的左侧且时,.4. 如图,一条数轴上点A表示-12,点B表示10,点C表示20.动点P从点A出发,以2个单位/秒的速度沿着数轴的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1个单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒.
(1)、当点在点的右侧且时,.(2)、当点在点的左侧且时,.4. 如图,一条数轴上点A表示-12,点B表示10,点C表示20.动点P从点A出发,以2个单位/秒的速度沿着数轴的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1个单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.设运动的时间为t秒. (1)、当t=秒时,点P运动到O点.(2)、当t=秒时,PO=2QB.
(1)、当t=秒时,点P运动到O点.(2)、当t=秒时,PO=2QB.三、解答题
-
5. 点A,B在数轴上分别表示有理数a,b,且我们将A,B两点间的距离记为AB.(1)、a= , b= , AB=;(2)、若点C在数轴上,且AC+BC=35,求点C表示的有理数;(3)、M,P,Q三点在数轴上,点O为原点,点M表示的数为12. P,Q两点分别从A,B两点同时出发,沿数轴的正方向运动,在到达点O前,P,Q两点的运动速度分别为4个单位长度/秒和2个单位长度/秒,点P经过点O后的速度变为原速度的一半,点Q经过点O后的速度变为原速度的2倍.设运动时间为t秒,当OP=QM时,求t的值.6. 如图1,已知点A、B、C、D在数轴上对应的数分别是a、b、c、24,其中a、b满足
 (1)、填空:a= , b= , c=;(2)、如图1,若点A、B分别同时以每秒4个单位长度、1个单位长度的速度匀速向右运动,假设经过t秒后,点A与点D之间的距离表示为AD
(1)、填空:a= , b= , c=;(2)、如图1,若点A、B分别同时以每秒4个单位长度、1个单位长度的速度匀速向右运动,假设经过t秒后,点A与点D之间的距离表示为AD问:当t为何值时,A、B之间的距离为2?
(3)、如图2,将数轴在原点O、点B和点C处各折一下,得到一条“折线数轴”.动点P从点A出发.以每秒3个单位长度的速度沿“折线数轴”的正方向匀速运动至点D,同时,动点Q从点D出发以每秒4个单位长度沿着“折线数轴”的负方向变速运动,该点在平地保持初始速度不变,上坡时速度变为初始速度的一半,下坡时速度变为初始速度的两倍,设运动时间为t秒. 若P、Q两点在点M处相遇,则点M表示的数为.7. 数轴上点A表示的数为10,点M,N分别以每秒a个单位长度,每秒b个单位长度的速度沿数轴运动,a, b满足|a-5|+(b-6)2=0. (1)、请直接与出a= , b=;(2)、如图1,点M从A出发沿数轴向左运动,到达原点后立即返回向右运动:同时点N从原点0出发沿数轴向左运动,运动时间为t,点P为线段ON的中点若MP=MA,求t的值:(3)、如图2,若点M从原点向右运动,同时点N从原点向左运动,运动时间为t时M运动到点A的右侧,若此时以M,N, O, A为端点的所有线段的长度和为142,求此时点M对应的数.8. 如图,点、、、由左至右依次均在数轴上,点在原点, , , , 点从点出发,沿方向以的速度运动,同时点从点出发沿方向向点匀速运动点运动到点时停止运动 , 设运动的时间为秒.
(1)、请直接与出a= , b=;(2)、如图1,点M从A出发沿数轴向左运动,到达原点后立即返回向右运动:同时点N从原点0出发沿数轴向左运动,运动时间为t,点P为线段ON的中点若MP=MA,求t的值:(3)、如图2,若点M从原点向右运动,同时点N从原点向左运动,运动时间为t时M运动到点A的右侧,若此时以M,N, O, A为端点的所有线段的长度和为142,求此时点M对应的数.8. 如图,点、、、由左至右依次均在数轴上,点在原点, , , , 点从点出发,沿方向以的速度运动,同时点从点出发沿方向向点匀速运动点运动到点时停止运动 , 设运动的时间为秒. (1)、点表示的数是 ,点表示的数是 点用含的代数式表示(2)、点在线段上,当时,点运动到的位置恰好是线段的中点,求点的运动速度.(3)、若点的运动速度为 , 经过多长时间、两点相距?9. 数轴是一种特定的几何图形,利用数轴能形象地表示数,在数轴的问题中,我们常常用到数形结合的思想,并借助方程解决问题.如图1,在数轴上,点A表示数 , 点C表示的数为2,点B表示的数为6.
(1)、点表示的数是 ,点表示的数是 点用含的代数式表示(2)、点在线段上,当时,点运动到的位置恰好是线段的中点,求点的运动速度.(3)、若点的运动速度为 , 经过多长时间、两点相距?9. 数轴是一种特定的几何图形,利用数轴能形象地表示数,在数轴的问题中,我们常常用到数形结合的思想,并借助方程解决问题.如图1,在数轴上,点A表示数 , 点C表示的数为2,点B表示的数为6.
 (1)、点P从点A出发,以2个单位/秒的速度向右运动,同时,点Q从点B出发,以1个单位/秒的速度向左运动,经过多久两点相遇?(2)、如图2,我们将图1的数轴沿点O和点C各折一次后会得到一个新的图形,与原来相比,线段和仍然水平,线段处产生了一个坡度,我们称这样的数轴为“坡数轴”,其中O为“坡数轴”原点,在“坡数轴”上,每个点对应的数就是把“坡数轴”拉直后对应的数.记“坡数轴”上A到B的距离为A和B拉直后距离:即 , 其中代表线段长度.在“坡数轴”上,上坡时点的移动速度变为水平路线上移动速度的一半,下坡时移动速度变为水平路线上移动速度的2倍.
(1)、点P从点A出发,以2个单位/秒的速度向右运动,同时,点Q从点B出发,以1个单位/秒的速度向左运动,经过多久两点相遇?(2)、如图2,我们将图1的数轴沿点O和点C各折一次后会得到一个新的图形,与原来相比,线段和仍然水平,线段处产生了一个坡度,我们称这样的数轴为“坡数轴”,其中O为“坡数轴”原点,在“坡数轴”上,每个点对应的数就是把“坡数轴”拉直后对应的数.记“坡数轴”上A到B的距离为A和B拉直后距离:即 , 其中代表线段长度.在“坡数轴”上,上坡时点的移动速度变为水平路线上移动速度的一半,下坡时移动速度变为水平路线上移动速度的2倍.①点P从点A出发,以2个单位/秒的速度沿着“坡数轴”向右运动,同时点Q从点B出发,以1个单位l秒的速度沿着“坡数轴”向左运动,经过多久,?
②点P从A处沿“坡数轴”以每秒2个单位长度的速度向右移动,当移到点C时,立即掉头返回(掉头时间不计),在P出发的同时,点Q从B处沿“坡数轴”以每秒1个单位长度的速度向左移动,当P重新回到A点所有运动结束,设P点运动时间为t秒,在移动过程中,何时?直接写出t的值.
10. 两个正方形在数轴上的位置如图1所示,若左边正方形沿数轴向左移动4个单位长度,右下角的点落在数轴上的点A处,右边正方形沿数轴向右移动6个单位长度,左下角的点落在数轴上的点B处,如图2所示. (1)、点A表示的数为 , 点B表示的数为 , 点A与点B之间的距离为 .(2)、如图3,左边正方形从点A出发,以每秒1个单位长度的速度沿着数轴向右匀速运动;同时右边正方形从点B出发,以每秒3个单位长度的速度沿着数轴向左匀速运动,当A′,B′两点重合时,两个正方形立即以原速度返回,回到各自原先的位置时停止运动,设运动时间为t(t>0)秒.
(1)、点A表示的数为 , 点B表示的数为 , 点A与点B之间的距离为 .(2)、如图3,左边正方形从点A出发,以每秒1个单位长度的速度沿着数轴向右匀速运动;同时右边正方形从点B出发,以每秒3个单位长度的速度沿着数轴向左匀速运动,当A′,B′两点重合时,两个正方形立即以原速度返回,回到各自原先的位置时停止运动,设运动时间为t(t>0)秒.①当A′,B'两点重合时,请求出此时A′在数轴上表示的数.
②在整个运动过程中,当A,A′,B′三点中有一点到其它两点距离相等时,请直接写出t的值.
11. 如图,在数轴上点表示数 , 点表示数 , 点表示数5,点到点的距离记为 . 我们规定:的大小可以用位于右边的点表示的数减去左边的点表示的数来表示.例如: .
 (1)、求线段的长;(2)、以数轴上某点为折点,将此数轴向右对折,若点在点的右边,且 , 求点表示的数;(3)、若点以每秒1个单位长度的速度向左运动,点以每秒4个单位长度的速度向左运动,两点同时出发,经过秒时, , 求出的值.12. 七年级数学兴趣小组成员自主开展数学微项目研究,他们决定研究“折线数轴”.
(1)、求线段的长;(2)、以数轴上某点为折点,将此数轴向右对折,若点在点的右边,且 , 求点表示的数;(3)、若点以每秒1个单位长度的速度向左运动,点以每秒4个单位长度的速度向左运动,两点同时出发,经过秒时, , 求出的值.12. 七年级数学兴趣小组成员自主开展数学微项目研究,他们决定研究“折线数轴”.探索“折线数轴”
素材1 如图,将一条数轴在原点O,点B,点C处折一下,得到一条“折线数轴”.图中点A表示-9,点B表示12,点C表示24,点D表示36,我们称点A与点D在数轴上的“友好距离”为45个单位长度,并表示为 .

素材2 动点P从点A出发,以2个单位长度/秒的初始速度沿着“折线数轴”向其正方向运动.当运动到点O与点B之间时速度变为初始速度的一半.当运动到点B与点C之间时速度变为初始速度的两倍.经过点C后立刻恢复初始速度.
问题解决
(1)、探索1 动点P从点A运动至点B需要多少时间?(2)、探索2 动点P从点A出发,运动t秒至点B和点C之间时,求点P表示的数(用含t的代数式表示);(3)、探索3 动点P从点A出发,运动至点D的过程中某个时刻满足时,求动点P运动的时间.13. 如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示 , 点B表示10,点C表示18,我们称点A和点C在数轴上相距28个长度单位.动点P、Q同时开始运动,点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,到点B之后立刻恢复原速,直至点C处停止运动;点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,到点O之后也立刻恢复原速,直至点A处停止运动.设运动的时间为t秒.问: (1)、当点P运动3秒时,点P在数轴上表示的数是;当点Q运动11秒时,点Q在数轴上表示的数是;(2)、动点Q从点C运动至A点需要时间秒;(3)、P、Q两点何时相遇?相遇时,求出相遇点M所对应的数是多少?(4)、在整个过程中,当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.(直接写出结果)14. 数轴上点表示 , 点表示 , 点表示点表示如图,将数轴在原点和点、处各折一下,得到一条“折线数轴”在“折线数轴”上,把两点所对应的两数之差的绝对值叫这两点间的和谐距离例如,点和点在折线数轴上的和谐距离为个单位长度,动点从点出发,以个单位秒的速度沿着折线数轴的正方向运动,从点运动到点期间速度变为原来的一半,过点后继续以原来的速度向终点运动;点从点出发的同时,点从点出发,一直以个单位秒的速度沿着“折线数轴”负方向向终点运动,其中一点到达终点时,两点都停止运动设运动的时间为秒.
(1)、当点P运动3秒时,点P在数轴上表示的数是;当点Q运动11秒时,点Q在数轴上表示的数是;(2)、动点Q从点C运动至A点需要时间秒;(3)、P、Q两点何时相遇?相遇时,求出相遇点M所对应的数是多少?(4)、在整个过程中,当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.(直接写出结果)14. 数轴上点表示 , 点表示 , 点表示点表示如图,将数轴在原点和点、处各折一下,得到一条“折线数轴”在“折线数轴”上,把两点所对应的两数之差的绝对值叫这两点间的和谐距离例如,点和点在折线数轴上的和谐距离为个单位长度,动点从点出发,以个单位秒的速度沿着折线数轴的正方向运动,从点运动到点期间速度变为原来的一半,过点后继续以原来的速度向终点运动;点从点出发的同时,点从点出发,一直以个单位秒的速度沿着“折线数轴”负方向向终点运动,其中一点到达终点时,两点都停止运动设运动的时间为秒.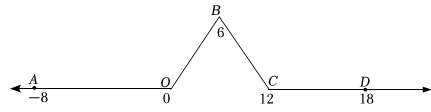 (1)、当秒时,、两点在折线数轴上的和谐距离为;(2)、当点、都运动到折线段上时,、两点间的和谐距离 用含有的代数式表示;、两点间的和谐距离 用含有的代数式表示: 时,、两点相遇;(3)、求当为多少秒时,、两点在折线数轴上的和谐距离为个单位长度.15. 如图
(1)、当秒时,、两点在折线数轴上的和谐距离为;(2)、当点、都运动到折线段上时,、两点间的和谐距离 用含有的代数式表示;、两点间的和谐距离 用含有的代数式表示: 时,、两点相遇;(3)、求当为多少秒时,、两点在折线数轴上的和谐距离为个单位长度.15. 如图 (1)、【材料阅读】
(1)、【材料阅读】如图①,数轴上的点A、B表示的数分别为﹣1、7,C是线段AB的中点.
点C表示的数是 .(2)、若点P、Q分别从点C、B同时出发,以每秒3个单位长度和1个单位长度的速度沿数轴正方向运动,则t秒后,点P、Q表示的数分别是 、 . (用含t的代数式表示)(3)、在(2)的条件下,若P、Q两点之间的距离为2,求t的值.(4)、【方法迁移】
如图②,∠AOB=140°,OC平分∠AOB.现有射线OP、OQ分别从OC、OB同时出发,以每秒15°和每秒10°的速度绕点O顺时针旋转,当OP旋转一周时,这两条射线都停止旋转.问经过几秒后,射线OP、OQ的夹角为30°,直接写出t的值.
-